汽车非线性悬架系统的分数阶PDμ控制研究

高 远，张一飞，袁海英，范健文

（1.广西科技大学 电气与信息工程学院，柳州 545006；2.广西科技大学 鹿山学院 汽车工程系，柳州 545006；3. 广西科技大学 广西汽车零部件与整车技术重点实验室，柳州 545006）

0 引言

汽车悬架是影响乘坐舒适性和操纵稳定性的重要部件。目前，可控悬架是现代车辆悬架技术发展的重要趋势。控制策略是实现悬架系统最优控制的保证，也是当前悬架控制系统研究发展的一个重要方面[1]。实际汽车悬架是受随机路面激励的非线性系统。迄今，人们结合汽车悬架系统模型，提出了许多单一的悬架系统控制方法，这些方法几乎涉及控制理论的所有分支，但各有优缺点[2]。

近年来，分数阶微积分理论被广泛应用于物理、材料、信号处理及自动控制等领域[3]。人们研究发现分数阶的控制器能获得比整数阶情形更优的控制动态性能和鲁棒性，这极大地促进了分数阶数学理论在控制领域中的应用发展[4]。迄今，人们提出了TID控制器[5]、CRONE控制器[6]、PIλDμ控制器[7]等不同类型的分数阶控制器。已有学者将分数阶理论应用于汽车悬架系统的设计及控制方面，但研究成果报道尚少。文献[8]提出CRONE悬架，采用分数阶阻尼的机械系统代替传统被动悬架中的弹簧和阻尼器，分析表明该悬架系统具有很强的鲁棒性和稳定度；文献[9]为提高汽车行驶平顺性，采用CRONE控制方法对不同荷载的悬架模型进行控制；文献[10]和文献[11]以分数阶“天棚”阻尼控制的车辆悬架为参考模型，分别提出悬架系统的自适应控制方法和滑模主动控制方法。

本文根据1/4车非线性悬架系统模型，采用线性系统频域分析和时间乘误差平方积分（ITSE）控制性能优化方法，设计出非线性悬架系统的分数阶PDμ控制器。仿真结果表明，在不同车速和等级道路行驶工况条件下，相比整数阶PD控制，分数阶PDμ控制器因其增加了可调的微分阶次参数，从而具有更好的汽车悬架系统控制性能和鲁棒性，可进一步降低悬架垂直振动位移、速度和加速度，更好地提高了车辆的行驶平顺性。

1 汽车悬架非线性系统模型

考虑图1所示的单自由度1/4车主动悬架系统模型。通过该图可得系统的微分运动方程[12]：

上式中： m是1/4车体质量，k1是车身刚度，Fzhi为滞后非线性阻尼力，x是车体垂直振动位移，x0为路面位移激励，u代表悬架系统的主动控制力。滞后非线性阻尼力Fzhi形为：

其中k2是非线性刚度系数，c1和c2分别代表线性阻尼系数和非线性阻尼系数。因此非线性悬架系统的动力学方程可进一步表示为：

本文所采用的非线性悬架系统参数如表1所示。

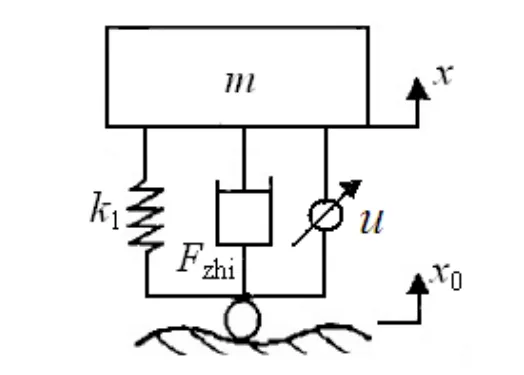
图1 1/4车悬架简化模型

表1 1/4汽车悬架系统模型参数

2 分数阶微积分简要介绍[13]

分数阶微积分运算是整数阶微积分理论的推广，整数阶情形是分数阶微积分的特例。目前，分数阶微积分运算虽然有多种不同的定义形式，但在实际应用中，Riemann-Liouville(R-L)定义是最常用的一种。对于一元函数f(t)的α阶微积分，其R-L定义为：

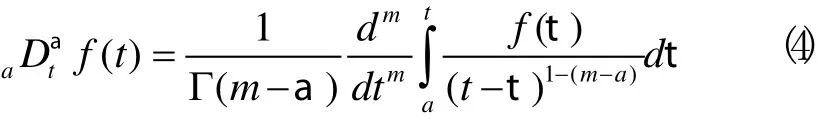
式中(m-1)＜α＜m, m为整数, a为f(t)的初始时

在零初始条件下，信号f(t)的R-L定义α阶微分的拉氏变换为[14]：

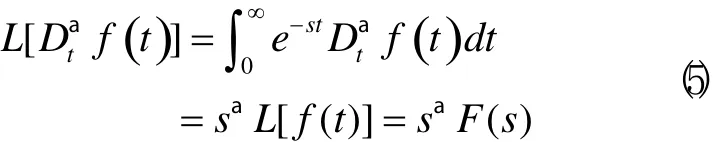
其中，F(s)为f(t)普通的拉氏变换，sα是复频域表示的α阶微分算子。

对于如下的分数阶常系数线性微分系统：

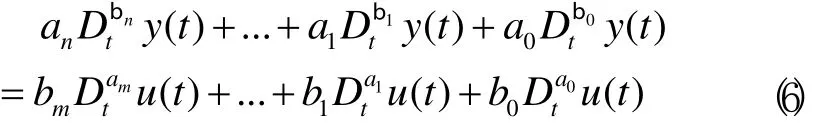
式中：y(t)和u(t)分别代表系统的输出响应和输入激励；αi, βj(i=0,1,…,n; j=0,1,…, m)为任意数，且有关系αn＞αn-1＞…＞α1＞α0，βm＞βm-1＞…＞β1＞β0；ai, bj(i=0,1, …,n; j=0,1,…, m)为常数。系统(6)的传递函数可表示为：

当s=jω，则传递函数对应分数阶系统的频率特性。

3 分数阶PDμ控制器

3.1 控制器数学模型

类似整数阶PD控制器，本文所采用的分数阶PDμ控制器，其传递函数形式为：

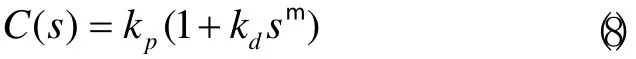
式中：kp和kd是控制参数，微分阶次 m ∈ ( 0,1]。当μ=1时，C(s)则变为传统的整数阶PD控制器。由式(8)可求出控制器的频率特性：

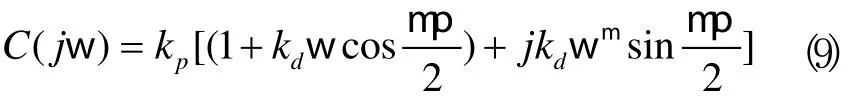
根据上式可进一步得到控制器的相频和幅频特性：

3.2 控制器设计准则

假定已知被控对象模型P(s)，期望的增益交越频率ωc和相位稳定裕度φm，为使控制系统满足稳定性和控制鲁棒性要求，根据交越频率和相位裕度的基本定义[15]，可得到控制系统开环传递函数G(s)=C(s)P(s)所应满足的相位和幅值准则[16]：

i 相位裕度准则

ii 系统增益变化的鲁棒性准则

iii 幅值准则

4 汽车悬架系统的分数阶PDμ控制器设计

4.1 PDμ控制器的频域设计方法

鉴于非线性悬架系统的强非线性和随机路面载荷会造成系统模型的结构及其参数辨识困难，同时为便于采用线性系统频域理论设计悬架系统的分数阶PDμ控制器，因此在不考虑随机路面激励和系统非线性环节作用的情况下，根据式(3)可以获得可控悬架系统的线性化运动方程：

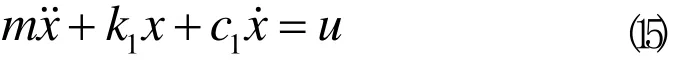
在零初始状态条件下，线性悬架系统的传递函数为：

式中： B1= c1/m，= k1/m。结合上式可分别得到线性系统的相频特性和幅频特性：

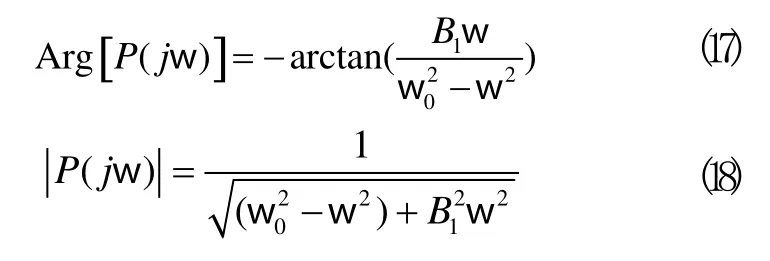
结合(10)、(11)、(17)和(18)，可求出控制系统开环传递函数G(s)=C(s)P(s)的相位及幅度频率特性：

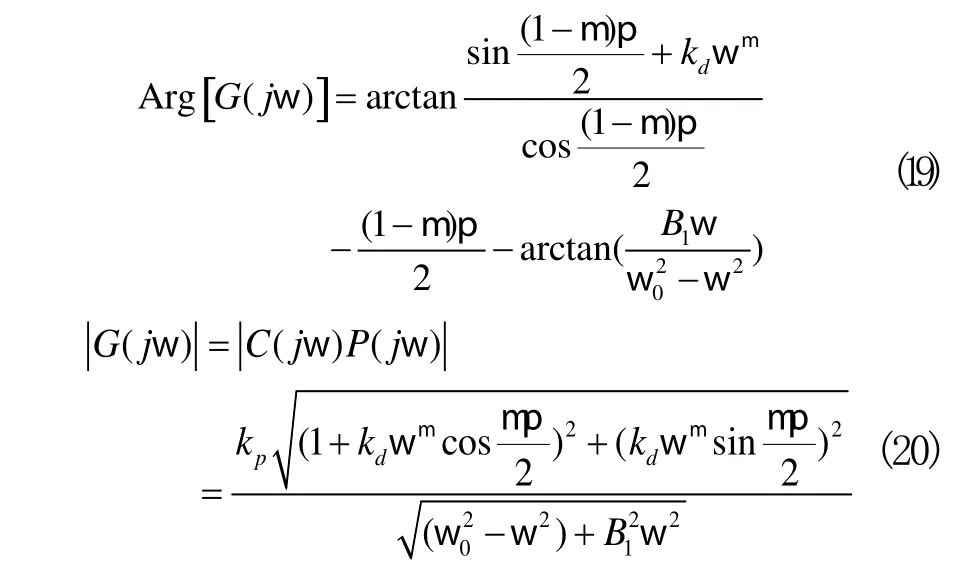
根据准则i，由式(19)可得到kd和μ之间关系：

根据准则ii和式(19)可建立起如下形式的kd方程

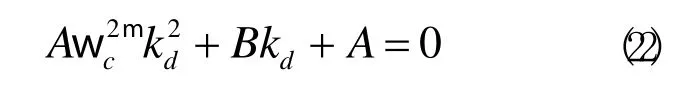
式中：

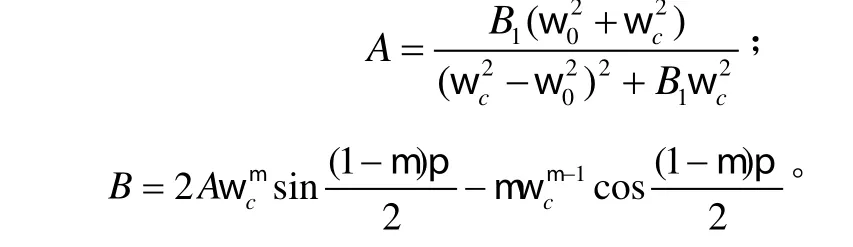
求解式 (22)可得到关于kd和μ之间的另一关系式：

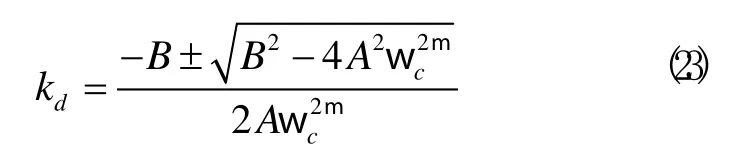
根据准则iii和式(20)，可求出kp和μ间的关系式：

显然，求解式(21)、(23)和(24)可得出kd、μ和kp。

4.2 图解方法求解控制参数

鉴于(21)、(23)和(24)表达式复杂，直接解析求解较困难，因此采用如下的图解方法步骤求出控制参数kd、μ和kp。

1)设定线性悬架控制系统增益交越频率ωc以及期望的相位稳定裕度φm；

2)根据 (21) 式和(23)画式出kd和μ间的关系曲线；

3)通过曲线交点确定kd和μ的图解值；

4)将kd和μ代入到 (24) 式计算出kp。

本文选取ωc=100rad/s，φm=60o，利用表1的系统参数值以及上述的控制参数求解步骤计算出kd=1.95，μ=0.68，kp=169.33。对于整数阶PD控制器(μ=1)，可设计出控制参数kd=1.1和kp=90.3。

图2和图3分别示出了整数阶PD控制和分数阶PDμ控制条件下，开环传递函数G(s)=C(s)P(s)的Bode图。比较图2和图3可见，两种控制器均满足所设定的交越频率和相位裕度设计要求，然而，相比整数阶控制情形，分数阶控制系统开环传递函数在谐振频率处的幅度峰值较小，谐振频率至交越频率间的幅频曲线负斜率小于-40dB/dec；同时，交越频率ωc附近的较宽频段范围内，相频曲线平滑且对频率的变化律为零，这表明分数阶控制器具有更好的控制稳定度及鲁棒性。

图2 整数阶控制的开环传递函数Bode图

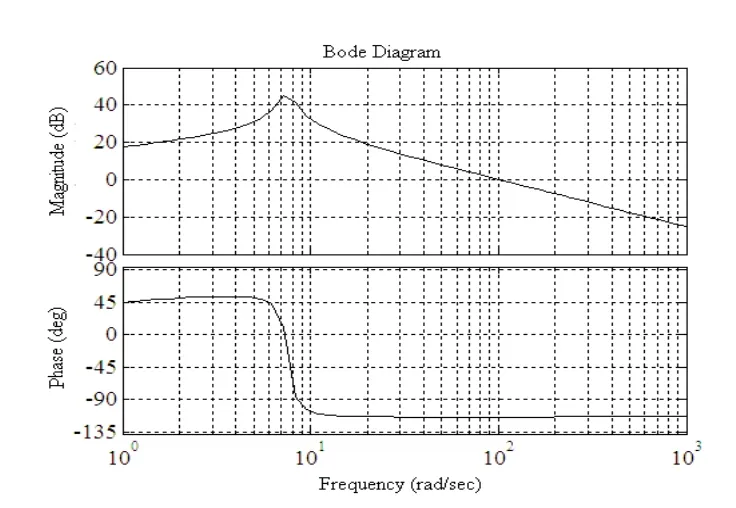
图3 分数阶控制的开环传递函数Bode图

4.3 控制器μ参数的优化

为提高汽车的行驶平顺性，以非线性悬架系统的垂直振动位移x和加速度x˙均趋于零作为控制目标，并构造如下形式的ITSE控制性能指标函数：

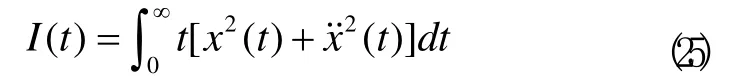
并考虑车辆非线性悬架系统受图4所示的路面冲击载荷作用，基于ITSE性能指标最小准则，利用Matlab优化工具箱的fmincon命令对分数阶控制器中的μ参数在(0,1]范围内进行调整优化。通过优化计算后，μ调整为0.97。因此，所设计出的非线性悬架系统PDμ控制器表达式为：

图5示出了三种不同PDμ控制器作用条件下，非线性悬架系统ITSE控制性能指标函数的时域演化曲线。根据图5比较可见，分数阶PDμ控制器的ITSE数值明显小于整数阶控制情形(μ=1)，且μ参数优化后的分数阶控制器(μ=0.97)具有更好的控制性能指标。

5 悬架系统的控制仿真结果及分析

在Matlab/Simulink环境下，对非线性悬架系统模型式(3)、PDμ控制器式(26)以及路面输入模型模块化程序实现。其中系统参数同上述，路面激励x0通过滤波白噪声方法产生[17]，分数阶微分数值计算采用Oustaloup滤波算法[18]。 为验证PDμ控制器的有效性和先进性，控制仿真中考虑汽车以不同车速在不同等级路面行驶的多种工况，以及对比被动悬架、整数阶PD控制方法的控制效果。

当车辆以70km/h行驶在C等级路面，图6、图7分别是悬架系统的垂直振动位移、速度x˙的时域响应曲线图。图8为悬架系统垂直振动加速度x˙的功率谱密度图。表2给出了不同等级路面和车速行驶工况情况下，悬架系统垂直振动位移、速度和加速度的均方根值。由这些图表比较可见，传统的整数阶PD控制和分数阶PDμ控制均能有效降低非线性悬架系统的垂直振动位移、速度和加速度，特别是汽车振动固有固有频率范围(0.7Hz～15Hz)以及人体敏感振动频率范围(4Hz～8Hz)的振动加速度值明显减小，提高了汽车的乘坐舒适性。相比整数阶控制情形，分数阶PDμ控制器对汽车非线性悬架系统具有更好的控制效果，这也表明分数阶PDμ控制器增加了可调的分数阶次参数μ，使得控制器的整定范围变大，控制被控对象更加灵活，通过合理设计控制器的kd、μ和kp参数，可获得非线性悬架系统更优的控制性能和鲁棒性。

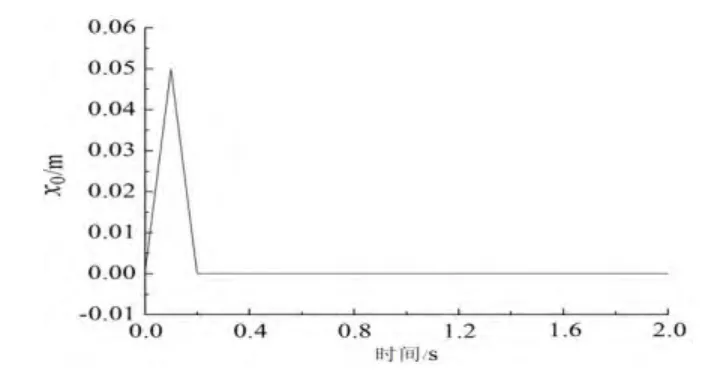
图4 冲击载荷波形图

图5 控制性能指标函数 (a) μ=1; (b) μ=0.68; (c) μ=0.97

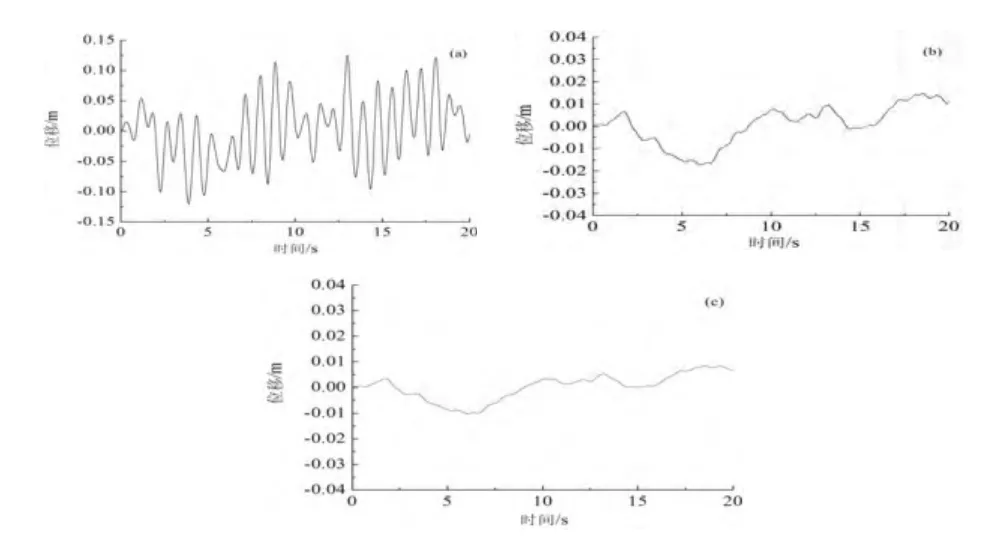
图6 振动位移时域响应曲线

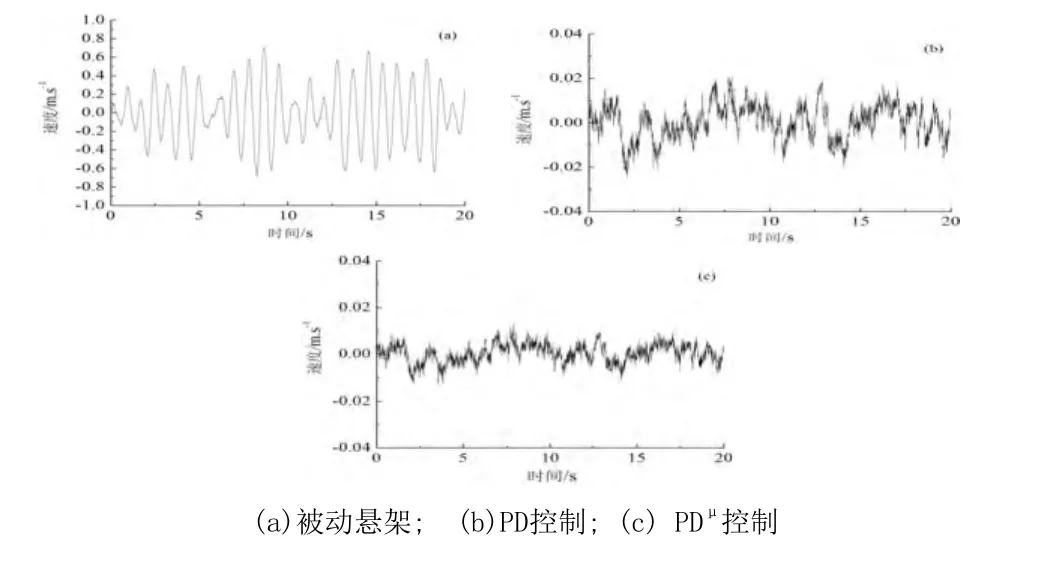
图7 振动速度时域响应曲线

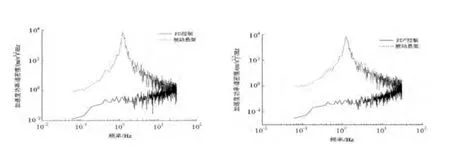
图8 振动加速度功率谱

表2 不同行驶工况条件下，汽车悬架系统垂直振动位移、速度及加速度均方根值

6 结束语

本文采用线性系统频域理论和ITSE控制性能指标优化方法，设计出非线性悬架系统的分数阶PDμ控制器。分数阶PDμ控制器增加了可调的分数阶次微分参数，相比整数阶控制情形，具有更为灵活的调节结构和更宽的整定参数范围，可获得更好的汽车非线性悬架系统控制效果和鲁棒性，尤其是分数阶PDμ控制器在降低人体敏感频率范围振动加速度方面具有明显优势；同时分数阶微积分运算工程可实现，因此，研究结果可望为设计可控悬架系统提高汽车乘坐舒适性，提供有用的控制方法参考。

[1] 高国生,杨绍普,郭京波.汽车悬架控制系统研究动态与展望[J].机械强度,2003,25(3):279-284.

[2] 寇发荣,方宗德.汽车可控悬架系统的研究进展[J].汽车工程,2007,29(5):426-432

[3] Bohannan, Gary W.Analog fractional order controller in temperature and motor control applications[J].J.Vib.Control,2008,14(9):1487-1498.

[4] 朱呈祥,邹云.分数阶控制研究综述[J].控制与决策,2009,24(2):161-169.

[5] Lurie J.Three–parameter tunable tilt-integralderivative (TID)controller[P].US Patent US5371670,1993.

[6] Ostaloup A,Melchior P.The great principles of CRONE control[C].Systems Engineering in the Service of Humans,Int Conf on Systems, Man and Cybernetics.Paris:Le Touquet,1993:118-129.

[7] Podlubny I.Fractional-order systems and PIλDμ controllers[J].IEEE Trans Automatic Control,1999,44(1):208-214.

[8] A.Oustloup, X. Moreau,and M.Nouillant. The Crone suspension control engineering practice[J].Journal of The International Federation of Automatic Control,1996,4(8):1101-1108.

[9] O. Altet,X. Moreau,M.Moze,P.Lanusse, etal. Principles and Synthesis of Hydractive CRONE Suspension[J].Nonlinear Dynamics, 2004, 38: 435-459.

[10] 陈宁,陈南,王乃洲,等.基于分数阶参考模型的车辆悬架自适应控制[J].南京林业大学学报(自然科学版), 2009,33(3):116-120．

[11] 陈宁,台永鹏,陈南.分数微积分理论在非线性车辆悬架滑模控制中的应用[J].动力学与控制,2009,07(3):258-264.

[12] 盛云,吴光强.汽车非线性悬架的混沌研究[J].汽车工程,2008:30(1):57-60.

[13] Oldham B,Spanier J. The fractional calculus[M].New York: Academic,1974.

[14] Podlubny I.The Laplace transform method for linear differential equations of the fractional order [J]. Functional Analysis,1997, 23(10):365-386.

[15] 胡寿松.自动控制原理[M].北京:科学出版社,2007:71-120.

[16] 王瑞萍,史步海,皮偌国. 基于分数阶控制器的PMSM恒速控制[J].华南理工大学学报(自然科学版),2012,40(3):191-125.

[17] 喻凡.车辆动力学及其控制[M].北京:人民交通出版社,2003.

[18] 薛定宇.控制系统计算机辅助设计第二版[M].北京:清华