2H桥单元组合逆变器复合控制策略
曹正博,王俊雄
(上海交通大学 船舶海洋与建筑工程学院,上海 200030)
0 引言
在要求严格的大型舰艇上,雷达声呐等系统需要可靠性高的中频电源。而目前较多采用的是直流交流发电机。这种直流-交流发电机的缺点是体积大,电能变换效率低,噪音高。因此高效率的中频交流逆变器正成为舰船电力系统不可逆转的趋势[1]。为了保证中品逆变器的波形质量与带宽控制,对开关频率的要求会非常高。如果采用多管并联,需要牵扯到复杂的开关管均流问题。为了避免这些,多电平的拓扑成为了较好的选择。而在多电平拓扑中,2H桥单元组合逆变器无论是从功率上还是开关数目上都要比其他拓扑具有优势,因此本文将研究一种2H桥单元组合逆变器的控制策略。
中频逆变器的开关频率与基波频率之比很小,普通LC滤波器不适用[2,3]。对于中频逆变器电源的执行器件,单机情况下使用IGBT模块,三相逆变器拓扑的容量是三相桥式容量的两倍,而且IGBT具有高输入阻抗,简单的驱动电路,本文的控制策略中将采用IGBT。就控制方法来说,目前有单闭环PID控制,双闭环PID控制,滞环控制,无差拍控制,状态反馈控制,滑模变结构控制,智能控制,同步旋转坐标变换控制,重复控制,P+谐振控制等[4]。这些控制都是各据优势,但也不乏各自的缺点,因此一种取长补短,互相渗透的复合控制方案是逆变器控制策略的发展方向。
本文将给出2H桥单元组合逆变器的拓扑,通过正弦波对称规则采样,找出谐波的成分,总结出多电平PWM波形的特点[5],为找出逆变器的控制策略提供依据。由于逆变器的谐波主要是高频谐波,且具有四倍频的效果。目前许多学者提出的控制方法大多针对50Hz-60Hz的低频逆变器,对于500Hz的中频则较少提出[6~8]。本文控制策略将选定于电压电流双环控制与重复控制器结合的一种复合控制策略,并在内环外环中采用P+谐振控制器来消除稳态误差和补偿3,5,7次谐波[9~13]。逆变器频率为500Hz,目标输出电压40V。
1 2H桥单元组合逆变器电路拓扑及数学模型
中频逆变器的开关频率不宜太高,因此多电平拓扑是很好的选择。和H桥单元组合逆变器与2H桥级联逆变器相比,2H桥单元组合逆变器拓扑的功率小,开关数目少,可控性更高。本文采用这种拓扑结构。图1显示的是2H桥单元组合逆变器单相的电路结构。

图1 逆变器单相拓扑
其中,Ed为直流母线电压,N为变压器匝比,L、C为滤波电感和滤波电容,R为逆变器的电路中等效电阻。逆变器输出电压UaT,UbT和UcT,电感电流为ial,ibl和icl,负载电流为iao,ibo和ico,而三相输出电压为Uao,Ubo和Uco。由Kirchhoff定律,得出:

单向系统仿真如图2,可看出2H桥电路输出为五电平,单相负载为平衡的正弦波。

图2 单相系统仿真波形
2 SPWM技术与谐波分析
为了使逆变器的输入正弦波有更好的效果,可以采用脉宽调制解调技术,与阶梯波技术相组合就是应用在三相逆变器中的SPWM技术[10]。传统的PWM技术的理论是基于面积等效原理。面积等效原理就是形状不同但冲量相等的窄波加在惯性环节上,其效果基本相同。这里的冲量指的是面积,效果基本相同指的是把输出信号进行Fourier变换后,除了高频段稍许不同,中低频十分相似。正弦波n等分后变成n个脉冲信号。由于这n个脉冲等宽不等高,所以可以把这些脉冲用等高而不等宽的矩形脉冲来代替,只要把矩形信号中点与原脉冲的中点重合即可。这样就得到了PWM波,因为是正弦波的等效,所以叫做SPWM波。通过调节矩形宽度来调节正弦波幅值。
在这里载波脉冲采用等腰三角形和双极性SPWM。其中载波与调制波的频率比叫做载波比;调制波与载波的峰值叫做调制度。现将直流电压的中点设为点O,直流母线电压为Ed。T11和T31组成桥臂1,T21和T41组成桥臂2。两个桥臂的中点分别为Q1和Q2,Q1和Q2相对O点的电压为UQ1和UQ2。当T11导通而T31截至的时候,UQ1=Ed/2,当T41导通而T11截至的时候,UQ1=-Ed/2。
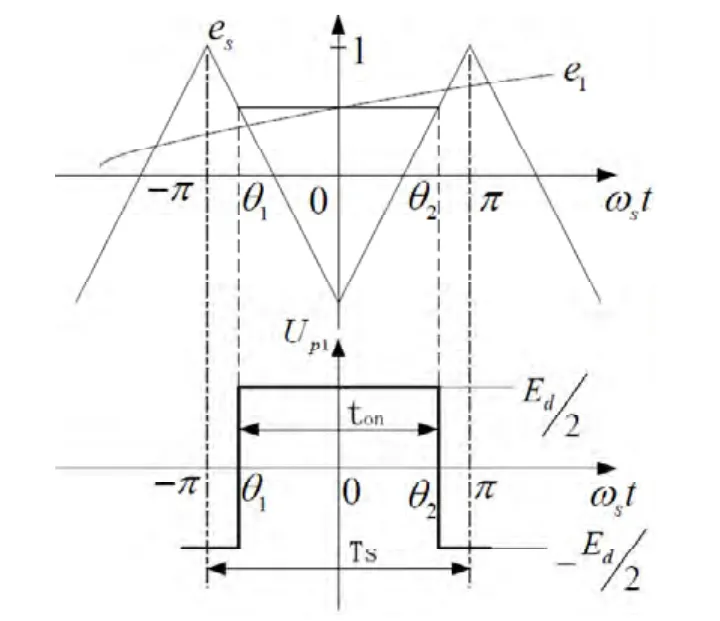
图3 对称采样规则PWM
ωs为采样角频率,采样周期为TS,脉冲宽度ton的大小是由中心点ωst=0时刻的调制波e1=mαsinω1t决定。可以得到下列式子:对
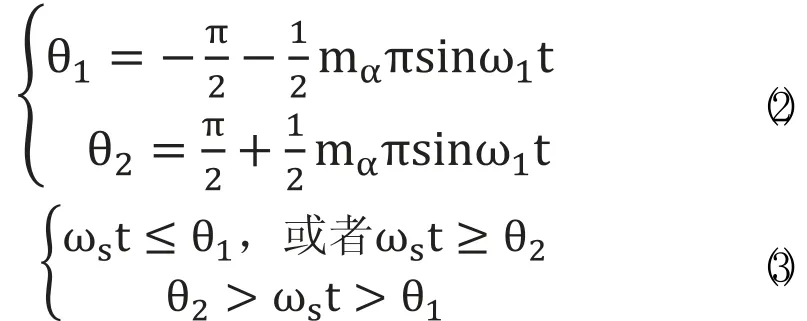
傅里叶变换后最终可以得到:
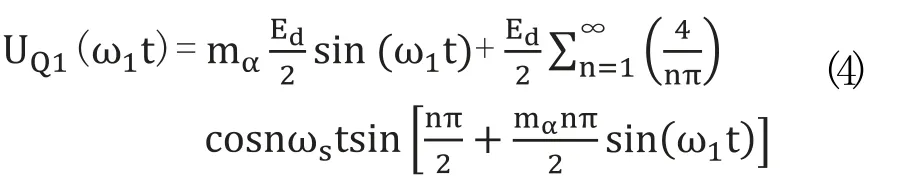
由于UQ2与UQ1相差半个周期所以:
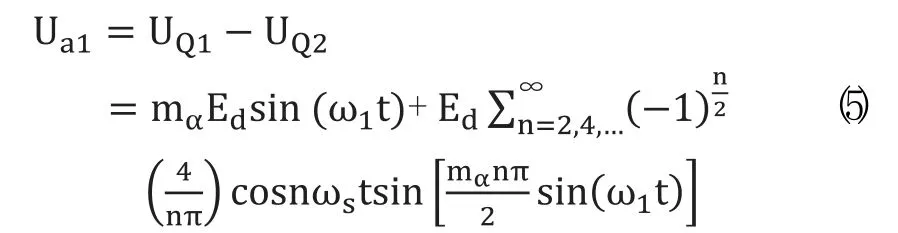
而上下两个桥的信号相位相差四分之一周期,那么逆变器a相电压UaT:
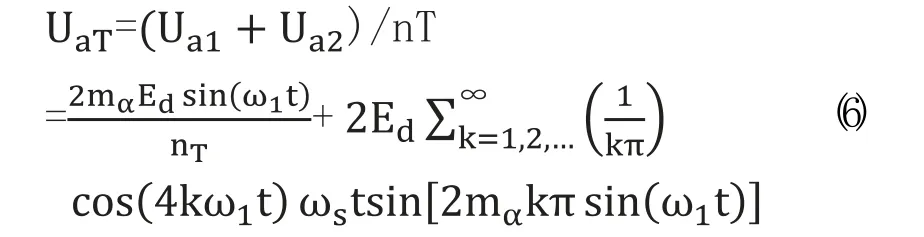

其中Jn为n次贝塞尔函数,nT为角频率,ω1和ωs分别是基波角频率与开关角频率,mα是幅值调制比。
从式中可以看出2H桥单元级联组合拓扑的电路谐波线电压基波幅值为2mαEd/nT,不存在低次谐波,谐波集中在4k附近,体现了四倍频的效果。
3 逆变器双环控制器
根据图1得出逆变器系统的等效框图,如图4所示。
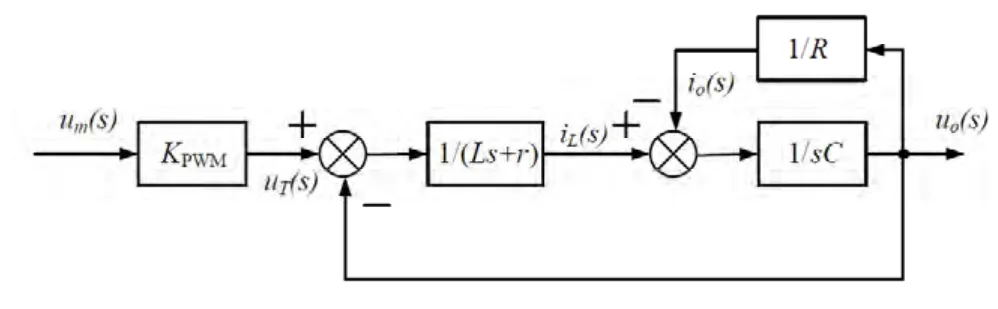
图4 单向系统等效框图
那么滤波器的传递函数为:
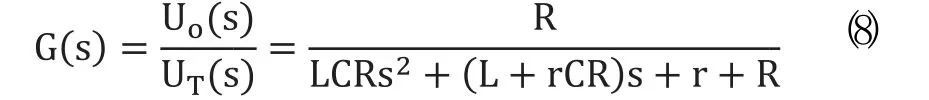
R为负载,L为滤波电感,C为滤波电容,r为滤波电感等效串联电阻。空载时,谐振频率C=400μF,r=0.01Ω,当R为1、10和100Ω时,系统Bode图如图5所示。

图5 滤波器Bode图(L=50μH,C=400μF,r=0.01Ω,R=1、10、100Ω)
可以看到,随着负载减小,系统从过阻尼向欠阻尼过渡,空载时震荡最为激烈,控制难度最大。因此需要针对空载来进行控制器设计。而根据系统的连续时间模型可以得出系统s域输出相应
关系:
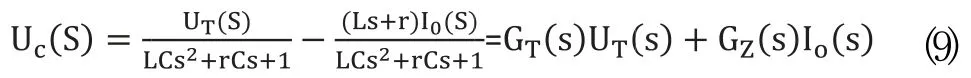
那么根据之前的系统参数,逆变器开环输出阻抗Bode图如图6所示。
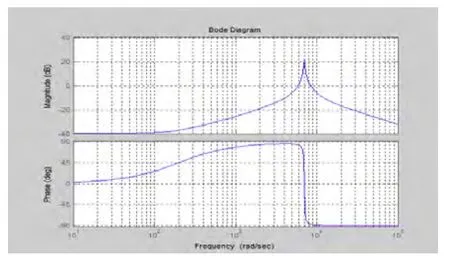
图6 逆变器开环输出阻抗Bode图
可以看出r很小,二阶震荡环节的谐振频率由LC决定,谐振频率数倍于基波频率,所以在低频处的输出阻抗随频率增加而增大。基波的输出阻抗由L和r决定。在负载电流不变时,频率越大,输出电压越小。在非线性负载条件下将难以保证良好波形。因此可以研究一种双环控制,内环反馈电容电流,外环反馈电压。
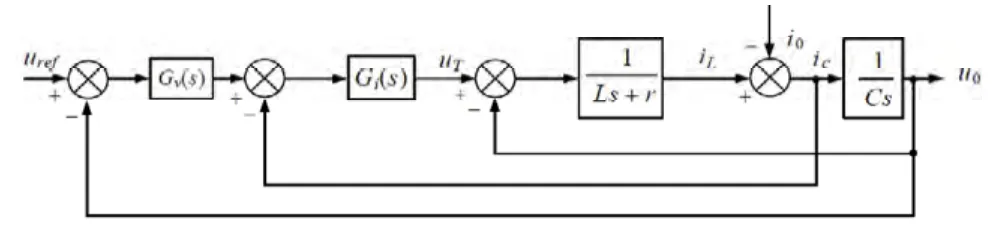
图7 电流电压双环反馈框图
系统传递函数:

在双环控制系统中,内环的电流要比外环的电压响应更快,因此在设计时,先设计内环控制器,再把内环看成一个外环的环节,再设计外环控制器。而且系统在空载时的稳定性最差,这里须确定空载时的参数。在大容量逆变器中,外环的电压带宽一般会限制谐振控制器,所以这里考虑在外环应用基波谐振控制器,内环应用其他谐波控制器。
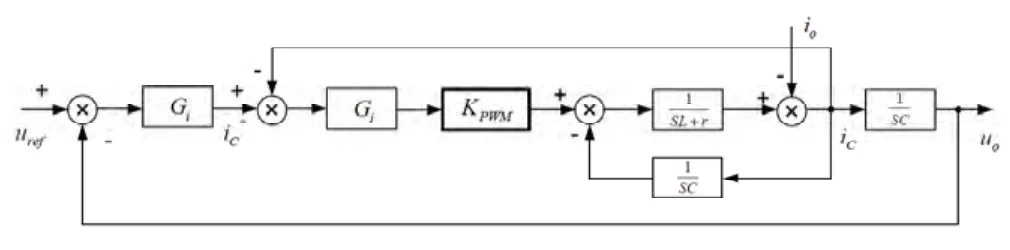
图8 逆变器单相双环控制器框图
内环开环传递函数和闭环传递函数为:

外环开环传递函数和闭环传递函数为:
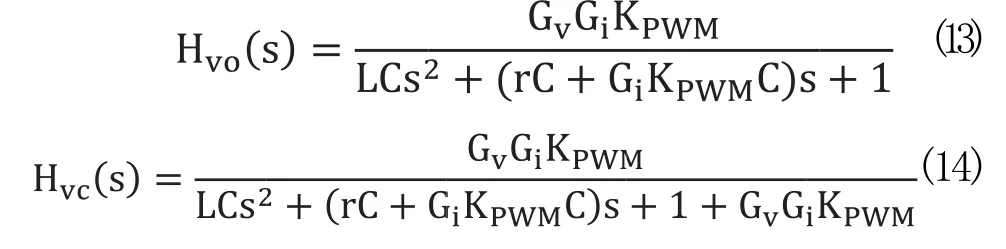
系统参数为:开关频率fz=5000Hz:直流母线电压Ed=50V,滤波电感L=50μH,滤波电容C=400μF,的等效电阻r=0.01Ω,输出频率f=500Hz,逆变器增益KPWM=20V,等效开关频率finv=20KHz。当Gv和Gi为比例控制器时,系统是二阶系统,阻尼比为0.707,根据实际的离散系统情况,GiKPWM取1.1212,Gv取3.6746。则系统的频域特性如图9。谐振频率为滤波器截止频率,外环具有较大的相位裕量和幅值裕量,系统对500Hz的信号有较大的稳态和相位误差。
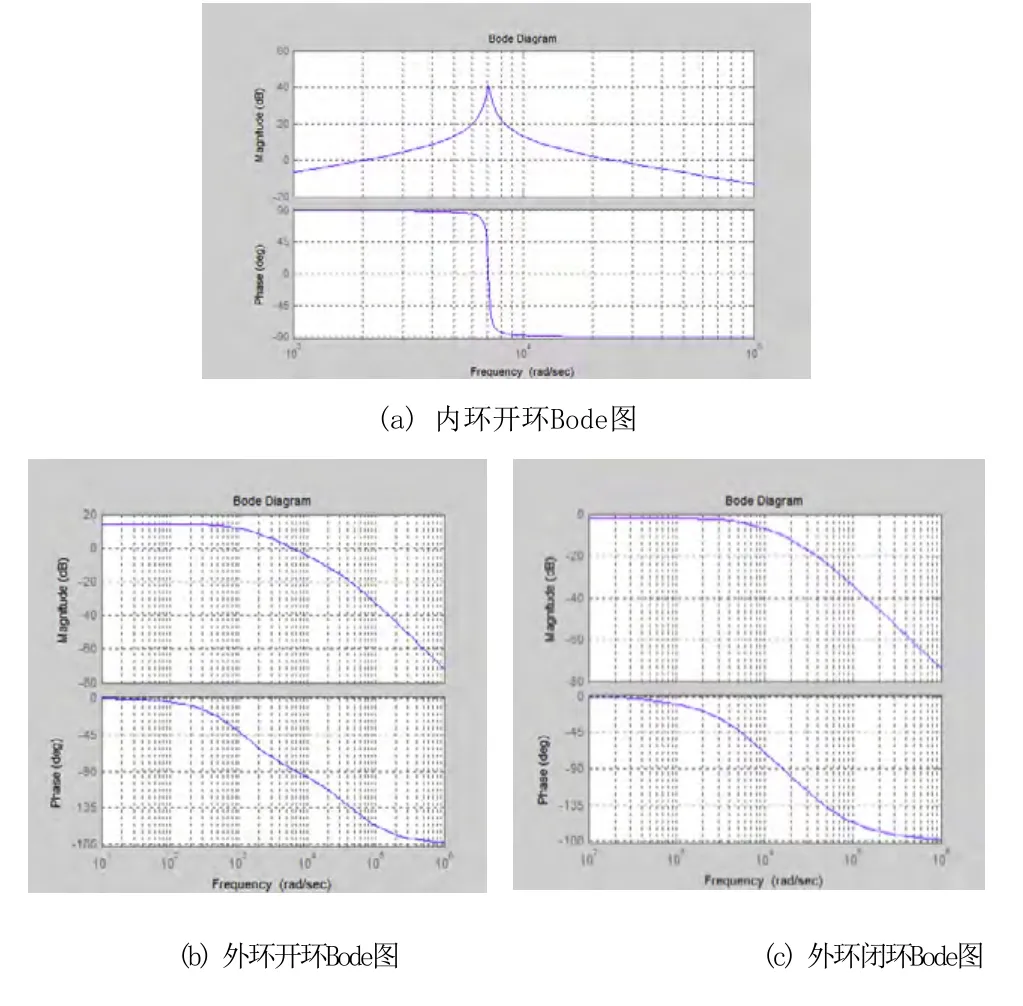
图9 双环控制Bode图
4 P+谐振控制器设计
系统的输出电压与参考电压和负载电流有直接关系,第二项为系统输出阻抗。在PWM逆变电源中,高次谐波一般会被滤波器滤掉,控制器只要考虑3、5、7、9次谐波即可。在谐波控制器与基波控制器在相同响应时间的情况下会发生耦合现象,所以把控制器分成三等级。第一等级为比例项KP,用来控制带宽。第二等级为基波谐振控来控制稳态误差。第三等级为谐波控制器图10给出了修正后的Gv(s)和Gi(s)。
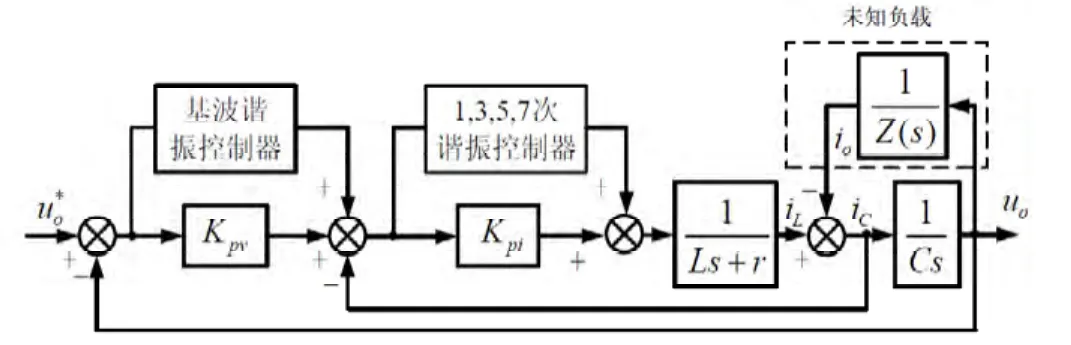
图10 内外环谐振控制器框图
在Gv(s)和Gi(s)修正后,即时负载为非线性,基波频率下的输出电压近似等于参考电压,而且电容电流的反馈量会使基波与谐波频率时的输出阻抗无限小,输出电压受负载的影响就会很小。
Gv(s)和Gi(s)传递函数如下:

则和的Bode图如图11所示。

图11 Gv (s)和Gi (s)的Bode图
将谐波控制器应用在三相逆变器中,逆变器参数如上文中所述。图12为线性负载的情况下输出电压和参考电压的波形。仿真的负载电阻大小为2Ω,负载电感的大小为350uF。可以看出输出波和参考波之间没有明显的复制和相位差,输出电压基本稳定在40V。图13为非线性负载时输出电流和输出电压的波形。非线性负载选取为二极管整流型的负载,电阻为2Ω。外接LC,其中电感大小为40uF,电容大小为2mF。从图中可以看出系统有良好的动态性能,输出电压同样稳定在40V。
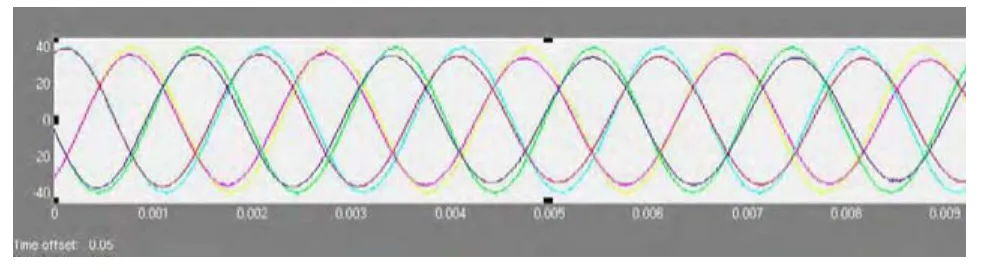
图12 线性负载时三相逆变器参考电压与输出电压波形

图13 非线性负载时三项逆变器的输出电压和输出电流
5 结论
针对中频逆变器的特点,本文建立了2H桥单元组合逆变器的拓扑结构和数学模型,通过SPWM的谐波分析找出谐波的特点。并以此建立了电压电流双环反馈的控制器。内环为电流反馈,使用3、5和7次谐波的P+控制器,外环为电压反馈,使用基波的谐振控制器。这种复合控制器有效地对各种谐波进行补偿抑制。在三相逆变器系统的仿真中得出了理论的适用性。
[1] 蔡坤,李耀华,胜晓松,等.高性能单相电压源逆变器的输出控制[J].电工技术学报,2005,20(1):104-107.
[2] Jensen U.B, Blaabjerg F, Pedersen J.K. A new control method for 400Hz ground power units for airplane[J].IEEE Transactions on Industrial Applications,2000,36(1):180-187.
[3] 宋强,刘文华,严干贵,等.大容量PWM电源逆变器的LC滤波器设计[J].清华大学学报(自然科学版),2003,43(3):345-348.
[4] 彭力.基于状态空间理论的PWM逆变电源控制技术研究[D].华中科技大学,2001.
[5] 王毅,李和明,石新春,等.多电平PWM逆变电路谐波分析与输出滤波器设计[J].中国电机工程学报,2003,23(10):78-82.
[5] Teodoescu R, Blaabjerg F, Liserre M. Proportionalresonant controllers and filters for grid-connected voltagesource converters[J].IEE Proc-Electr.Power Appl.2006,153(5):750-762.
[6] 龚幼民,胡慎敏.电力传动与变频电源[A].第十五届全国电源技术年会论文集[C].2003,736-738.
[7] 谢力华,苏彦民.正弦波逆变电源的数字控制技术[J].电力电子技术,2001,12,35(6):51-55.
[8] 雄蕊,朱秋花,王国峰.SPWM逆变电源输出电压波形重复控制技术的研究[J].电力电子技术,2001,2:45-47.
[9] Zmood D.N,Holmes D.G. Stationary frame current regulation of PWM inverters with zero steady state error[J].IEEE Transactions on Power Electronics, 2003,18(3):814-822.
[10]Escobar G,Stankovis A.M, Mattavelli P. Dissipativitybased adaptive and robust control of UPS in unbalanced operation[J].IEEE Transactions on Power Electronics,2003,18(4):1056-1062.
[11]Liserre M,Teodorescu R, BLaabjerg F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values[J].IEEE Transactions on Power Electronics,2006,21(1):263-272.
[12]张纯红,张婧,邬伟扬,等.基于Delta算子的谐振控制器实现高频链逆变器波形控制[J].电工技术学报,2008,23(7):81-85.
[13]李建林,许鸿雁,高志刚,等.级联H桥五电平变流器工况分析与验证[J].电工技术学报,2007,22(4):85-91.

