基于小样本集推理的雷达信号多维分选技术

王 懋，王 锐，徐 祎，张海黎

（1.电子工程学院，安徽 合肥 230037；2.北京地区军事代表室，北京 100083）

0 引言

在电子情报侦察系统（ELINT）、电子支援系统（ESM）和反辐射导弹（ARM）中，未知辐射源环境下的雷达信号分选占有重要的地位［1］。在未知辐射源环境下无法得到训练样本，雷达脉冲信号分选是利用脉冲信号参数的相关性实现的。比较经典的算法有直方图法、PRI变换法以及平面变换法，它们采用一维、二维方式分选，无法直接利用现有的载频、脉冲到达时间、脉冲宽度、脉冲幅度、到达角（方位角和俯仰角）五个传统参数进行多参数分类，效率受到影响。而现有多参数聚类的多维分选方法，又存在最佳分类个数和误差范围的选择问题。本文提出了一种基于小样本集推理的雷达信号多维分选技术，充分利用已有的雷达信号描述向量来达到最佳分选效果，避免目前经典算法所带来的问题，得到具有良好推广性的分类器。

1 基于小样本集推理的支持向量聚类

1.1 小样本集推理

小样本集推理是一种非参数判别分类的学习方法。20世纪60年代出现的非参数判别分类的学习方法，在应用统计学的基础上结合了模式识别和计算机科学，克服了传统参数判别分类的学习方法不能解决的一些问题，如“维数灾难”，样本较少时无法精确获得概率密度函数的问题。20世纪末由Vapnik等人提出了针对小样本集推理的一般理论及其方法。对学习机器函数集的容量进行控制，从而实现有限样本的有效学习，找到推广性好的学习机器。

小样本集推理的基本原则是绕过参数估计，由训练样本集提供的信息直接确定决策域，经典方法为基于统计学习理论的支持向量机SVM方法。遵循此原则的逻辑思路再向前发展一步，就得到超出归纳的一种推理思想——转导推理。利用SVM方法中的一些基本技术如核函数，超球体等，结合其他的一些聚类算法的思想，小样本集推理甚至可以延伸到无监督学习的领域——支持向量聚类。

在雷达信号多维分选中，可以将脉冲雷达目标信号进行多维特征表示，在多维空间中采用一些分选算法实现目标分选智能化。同时这些目标信号的先验知识往往是有限的，属于小样本集范畴，因此，把小样本集推理技术应用到雷达信号多维分选中具有比较重要的意义。

1.2 支持向量聚类算法概述

在聚类算法中只有一簇未标号的数据对象，所以只用一类支持向量机。用任意封闭曲面（超球体）包住经过Φ非线性映射后的一簇数，并要求超球体尽可能紧地包住这簇数。Tax等人提出了用核函数的方法进行数据域描述，即基于Gauss核的SVDD（Support Vector Domain Description）算法。在国内，张钹等人用领域覆盖的概念描述数据几何意义。Ben－Hur等将SVDD算法进一步发展为一种新的无监督非参数型的聚类算法：支持向量聚类（SV Clustering）［2－3］。

SV Clustering算法分为两部分：形成SV的聚类边界的SVM训练部分和聚类形成部分。其中SVM训练部分负责新知识模型的训练，包括Gauss核函数宽度系数的优化、Lagrange乘子的计算、Hilbert空间最小包络超球体半径的计算和有界支持向量（BSVs）与支持向量（SVs）的选取。聚类形成部分首先生成聚类标识关联矩阵，再通过DFS（Depth first Search）算法根据关联矩阵进行聚类。

该算法解决了常规聚类算法的聚类中心数和迭代最大次数等参数设定的问题，在实际仿真中发现对数据对象的几何分布要求不高，不仅能解决常规聚类算法解决的问题，而且还能很好地应用在常规聚类算法不宜进行的地方。

1.3 聚类边界

通过支持向量机训练，在升高维数特征空间中得到包括所有数据点的最小包络超球体边界。在输入空间内定义输入数据点｛xi｝⊆χ，χ⊆Rd，使用一个非线性映射Φ将｛xi｝分别映射到一个高维的空间，从而｛Φ（xi）｝呈现更规则的形式。

在高维特征空间中找到最小半径为R，为了防止有噪声影响，将边界进行软化引入松弛因子ξj，变成了一个求有约束条件的最优值问题：

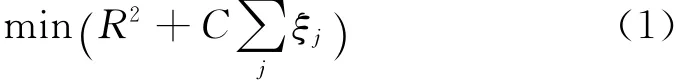
约束条件：

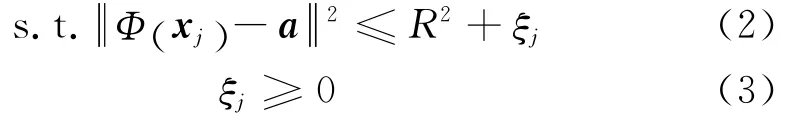
式中，R是超球半径，a是超球中心，‖·‖是欧氏距离范数，C是惩罚系数。C值决定超球外点数目，C越大，外点越少（噪声点出现的越少）。

利用Lagrange乘数法，解决式（1）～（3）最优化问题。分别得到：

一旦样本数据和非线性映射给定，超球心向量a、参数βj和球半径R就都不会变化。

根据式（4）～（6）化解最优化问题中只剩βj参数，再转化为Wolf对偶二次规划问题：

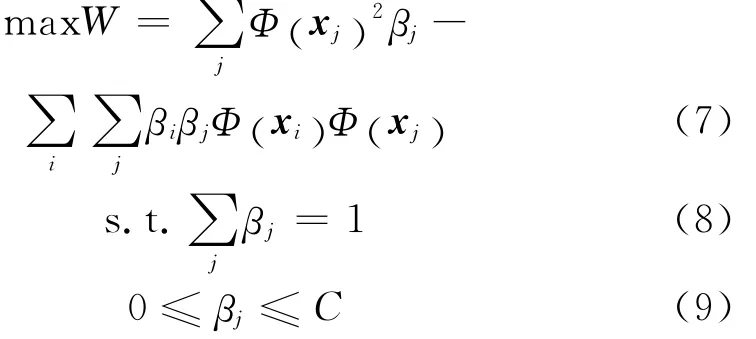
最优解满足Karush－Kuhn－Tucker条件：

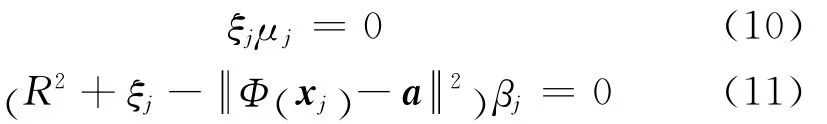
将式（7）中的内积，用满足Mercer条件的核函数代替。本文使用Gauss核：

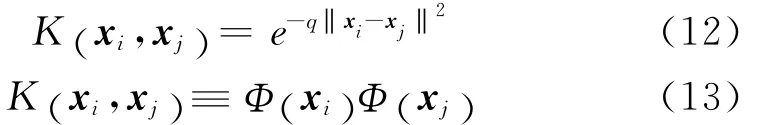
则Wolf对偶二次规划问题式（7）～（9）变为：

解式（1 4）得到βj，这样输入空间对应的高维特征空间就确定了。同时输入空间中的数据点对应在特征空间中的位置也确定了，根据上面的分析，可得到表1。

表1 参数βj与相对包络超球的位置对应关系

通常直接计算特征空间中任一点到球心的距离，将式（6）、（14）代入距离定义式得：

一般聚类半径定义为：

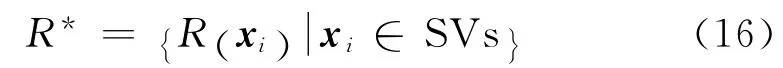
实际上是求均值：

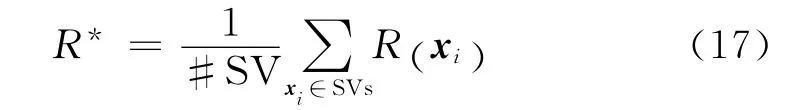
式中＃S V表示支持向量的个数。

聚类边界可由输入数据空间中满足R（x）＝R＊的所有数据点的等高线构成。集合为聚类边界，B S V s在边界外。

1.4 聚类规则

现在知道每个点到超球球心的距离，具体哪些点属于哪个簇是还需要进一步处理。研究发现如果两个输入点属于同一个簇，那么两个点的连接线上所有点，在高位特征空间中，都不会位于球外。反过来考虑，给定一对样本数据点xi和xj，连线当中如果有一个断点y，使R（y）＞R＊，则两个数据点非同一簇。H u r－B e n根据这种思想，构造一个n×n关联矩阵A：

关联矩阵中邻近元素的集合即为聚类，如果只有一个元素，则标记为噪声。

2 雷达信号小样本集多维分选

2.1 分选参数的提取

对侦察雷达获得的数据，首先进行分选参数的提取，它是后续分选工作的基础。通过前端精确测量仪器，可以测频、测时间和测方向。接着经过特征提取、信号去交错、脉冲模式提取、跟踪器等前端预处理。最后得到分选参数。

2.2 小样本集分选技术实现

本文将雷达脉冲描述字代入小样本集推理算法支持向量聚类中。

Step1 将所有描述字表示的参数归一化。这样方便对不同范围的数据进行统一的分选。

Step2 开始形成SV聚类边界，即SVM训练部分。

1）对归一化数据进行空间分析，本文采用对Hilbert空间中数据之间的欧几里德距离分析，得出分类效果最佳的rbf（径向基函数）核函数宽度系数。这里计算所有样本欧式距离的最大值和最小值，核函数宽度系数γ取最小值和最大值倒数的平均值，γ＝（min（distance）＋ （max（distance））－1）/2。

2）参数C的大小决定了野值点的数量，随着C（C≤1）值的减小，野值点的数量会增加，可以平滑聚类边界，但同时经验风险变大。由于SVC中Lagrange乘子βj归一化了，所以C＞1对生成βj无影响，同时SV聚类边界中不存在BSV，BSV对应的βj＝C。故C＝1。

3）通过支持向量训练，在升高维数特征空间中得到包含所有数据点的最小包络超球体边界。获得Lagrange乘子β，代入聚类半径表达式中得到半径R。由于半径有一定波动，这里取均值。

Step3 形成支持向量聚类，即生成聚类标示关联矩阵。在已有数据点xi，xj连线间插入新数据点yk，通过计算该新数据点yk是否处在聚类边界里面来判断已有数据点之间有无关系。如果R（yk）≤R，则xi，xj有关联；否则无关联。

3 仿真试验

为验证基于小样本集推理的雷达信号多维分选方法的有效性，本文仿真产生一系列雷达脉冲数据并对其进行预处理，预处理后实验数据如表2所示。

表3列出了基于小样本集推理的雷达信号多维分选方法和直方图分选方法的正确率和消耗时间的对比情况。其中，分选准确率＝（总脉冲数－漏分选脉冲－误分选脉冲）/总脉冲数×100%。

4 实际数据验证

通过55个卫星接收到的雷达脉冲校验数据（见表4），进一步验证本文算法的推广性和可靠性。

第一步：采用（x－min）/（max－min）进行数据的归一化。得到六维向量（载频RF，脉冲到达时间TOA，脉冲宽度PW，脉冲幅度PA，方位角AZA，俯仰角PIA）55个。

第二步：将数据代入SVC算法中。通过计算得到核函数宽度γ＝0.29162，并且设置惩罚系数C＝1。通过对最优函数的计算得到Lagrange乘子β，如图1（a）所示。同时得到相应的聚类包络的半径R，半径R＝0.54482。如图1（b）所示。

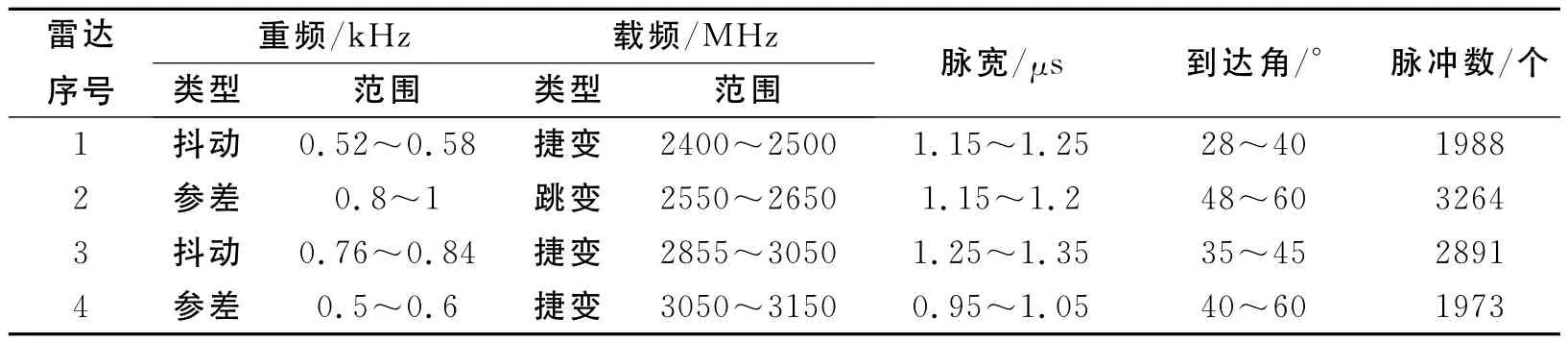
表2 仿真雷达脉冲信号参数表

表3 直方图法和本文方法的分选准确率和总执行时间

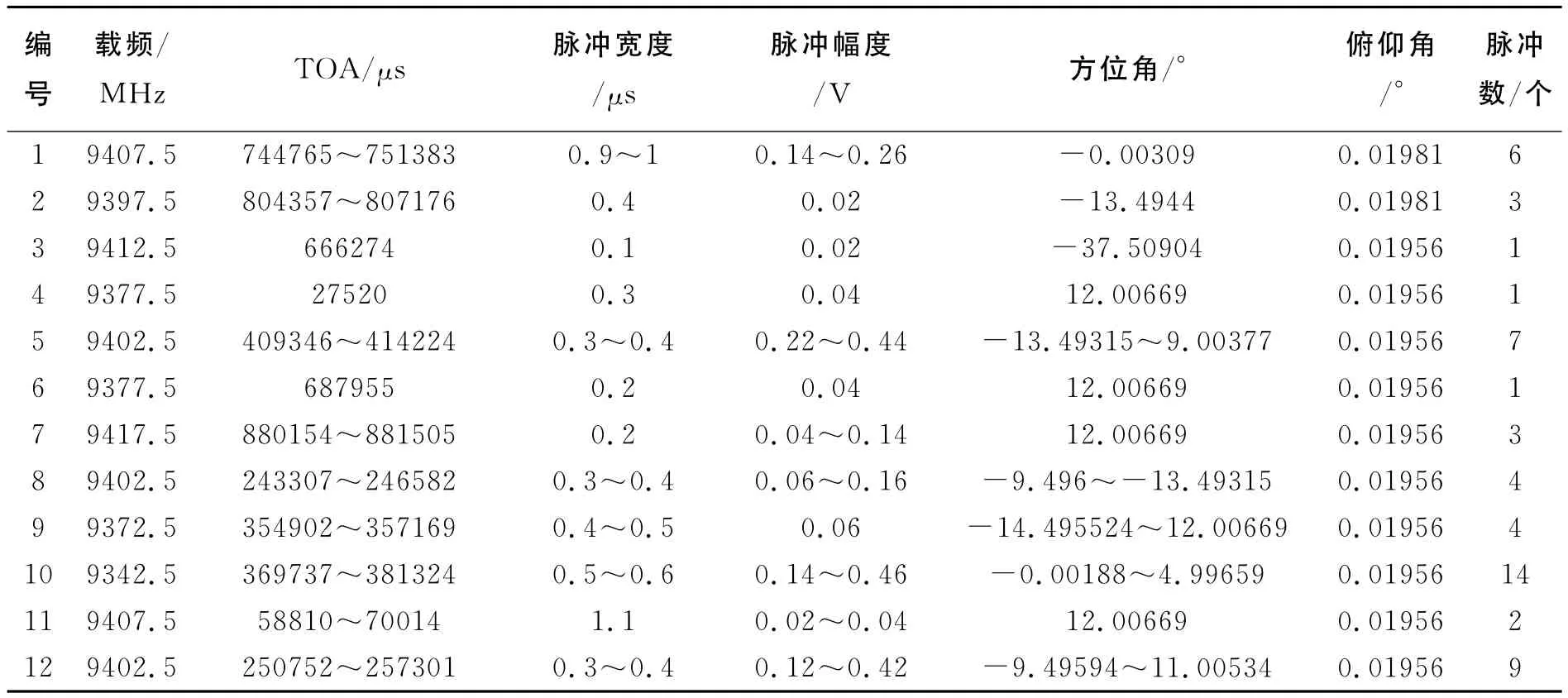
表4 55个雷达脉冲校验数据

第三步：依据最优包络超球体的球心位置和半径，通过算法聚类形成方式，得到相应的标示关联矩阵。通过该矩阵，对PDW进行聚类分选，得到以载频RF和到达时间TOA为坐标的雷达信号分布图，如图2所示。对分选脉冲信号总数进行编号统计得到分选结果统计直方图，如图3所示。

图1 Lagrange乘子/距离包络球心距离与雷达脉冲对应关系

第四步：进行聚类效果分析，主要对分选准确率进行分析。分选准确率＝（准确分选的总脉冲数/脉冲总数）×100%。得到SVC聚类分选方法分选结果统计表，如表5所示。由总分选准确率可看出其分选效率优于传统的直方图方法。

图2 雷达二维信号分布图

图3 雷达信号分选结果统计直方图

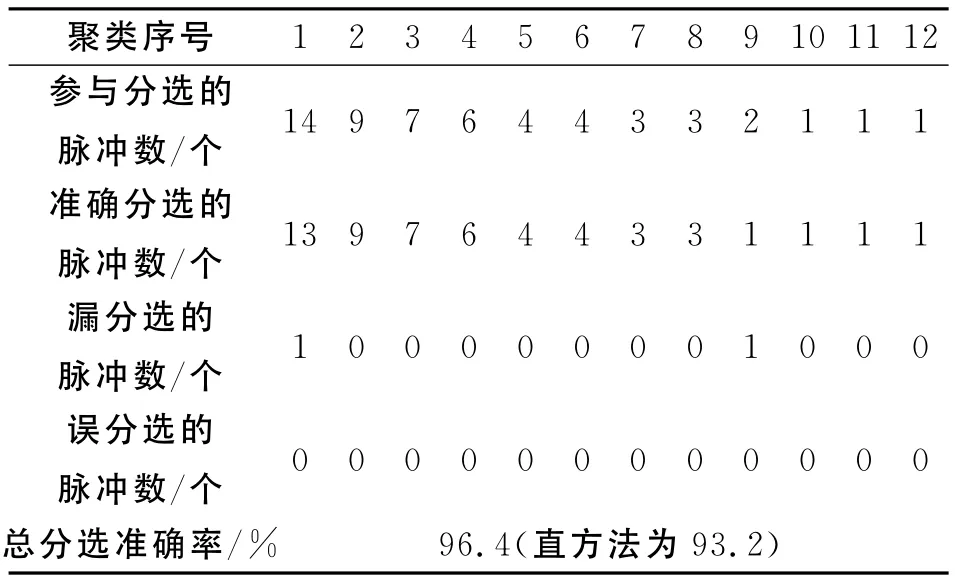
表5 雷达脉冲分选结果统计表

5 结束语

高分选效率且充分考虑最佳分类个数和误差范围均衡的聚类算法是星载雷达信号分选不可或缺的有效工具。本文提出基于高精度测量得到的五个脉冲描述字PDW＝（脉冲到达方向（方位角AZA/俯仰角PIA），载频RF，脉宽PW，到达时间TOA，脉幅PA），利用小样本集推理技术——支持向量聚类方法，生成雷达信号分类器。该方法克服了未知辐射源环境下不能获取大量训练样本的困难，并且采用多参数分选，与传统的直方图方法相比，分选效率更高。

［1］Wiley RG.ELINT：the interception and analysis of radar signals［M］.2ed.Boston，MA：Artech House，2006：317－356.

［2］Hur AB，Horn D，Siegelmann HT，et al.Support vector clustering［J］.Machine Learning Research，2001（2）：125－137.

［3］Hur AB，Horn D，Siegelmann HT.A support vector method for hierarchical clustering［J］.Advances in Neural Information Processing Systems，2001（13）：367－373.