存在无风险证券的投资组合选择模型及其应用研究

隋云云，马树才

（1.辽宁大学 经济学院，辽宁 沈阳 110031；2.潍坊学院 数学与信息科学学院，山东 潍坊 261061）

存在无风险证券的投资组合选择模型及其应用研究

隋云云1,2，马树才1

（1.辽宁大学 经济学院，辽宁 沈阳 110031；2.潍坊学院 数学与信息科学学院，山东 潍坊 261061）

基于可能性理论，利用可能性均值作为对证券投资组合收益的度量，以可能性方差作为证券投资组合风险的度量，建立了存在无风险证券情况下的投资组合选择模型，最后结合实例说明该模型的实用性。

可能性均值；可能性方差；无风险证券；三角模糊数

一、引言

Harry Markowitz于1952年在其发表的论文[1]中率先提出均值-方差模型，将不确定条件下的投资组合问题模型化，此后，许多学者都是在这一理论基础上展开投资组合理论的研究工作[2-4]。由于在Markowitz模型中需要计算所有风险证券之间的协方差，计算量比较大，为了克服这一困难，许多学者提出了一些新的组合投资模型。如：Markowitz[5]提出的以半方差作为风险函数的度量，Konno和Yamazaki提出的以绝对偏差作为风险函数的度量，以及Cai等提出的L∞风险函数。

传统的均值-方差模型建立在概率论的基础上，用随机变量来描述风险资产未来收益的不确定性，但是由于金融市场的复杂性，且投资受到如投资环境、投资者年龄、性别及投资者的信息认知能力等诸多模糊因素的影响，模糊因素对投资市场的影响已逐渐受到关注。近年来，许多学者在模糊投资组合选择方面也做出了大量的研究工作。Tanaka和Guo于2000年在文献中将证券的收益率看作可能性变量，根据专家给出的历史收益率的样本与未来证券市场状态之间的相似程度，并以此确定投资组合收益率的可能性分布，提出了可能性中心差值模型。Calsson和Fullér在文献中给出了模糊数的上下可能性均值的概念，以及两种可能性方差的概念；随后Calsson和Fullér又在文献中利用第一种可能性方差基于效用函数给出了一种证券投资组合模型及其可能性解法。

本文利用Calsson和Fullér中所定义的第一种可能性方差，建立了存在无风险证券情况下的投资组合选择模型，并结合实例说明该模型的实用性。本文将按如下思路进行：第二部分将介绍三角模糊数的定义及性质；第三部分给出模糊数的可能性均值、可能性方差以及它们的性质；第四部分将利用可能性均值作为对证券投资收益的度量，以可能性方差作为对证券投资风险的度量，建立一种新的可能性均值-方差模型，并研究可能性分布为三角模糊数情况下的组合投资模型的形式及求解方法；第五部分将给出一个实例说明该模型的实用性。

二、预备知识

（一）相关定义

定义1[6]设是论域X到[0,1]的一个映射，即

定义 2[6]设∈ F(X)，α∈ [0,1]，令 Aα=则称Aα为模糊集的α-截集，或称为的α-水平集。

定义3[6]∈F(X)称为模糊数，若

（2）∀α∈(0,1]，有Aα为闭区间。

定义4[6]∈F(X)且的隶属函数为

（二）有关性质

性质1[6]（线性运算性质）

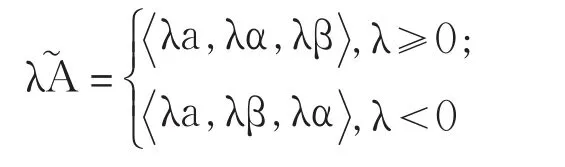
三、模糊数的可能性均值与方差的定义、性质

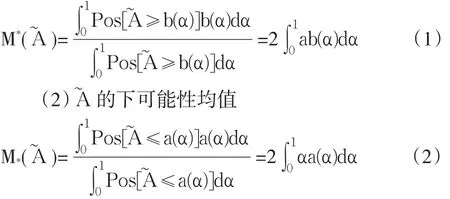
其中Pos表示可能性，具体推导过程见文献。

从而由定义5及定义6可知

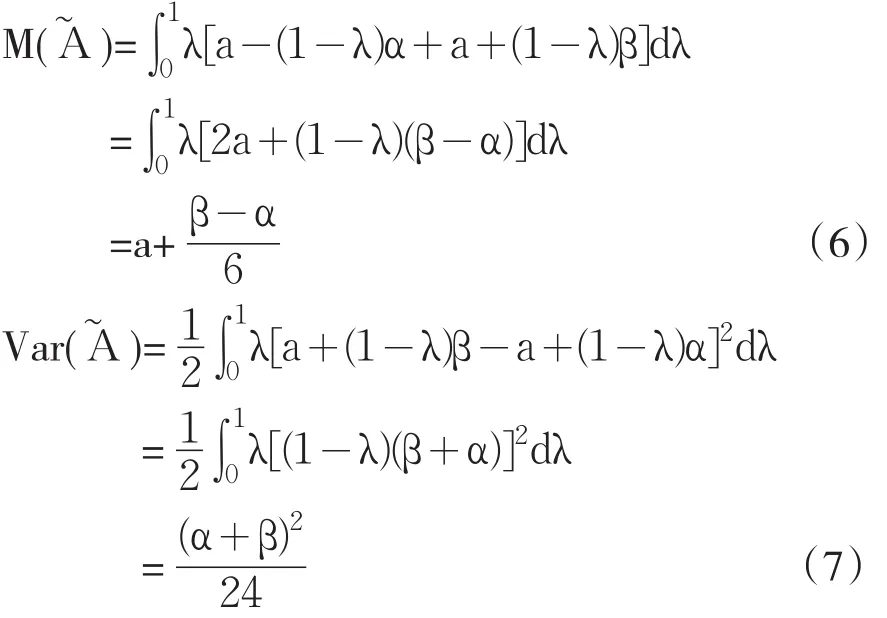
从而

四、模型建立

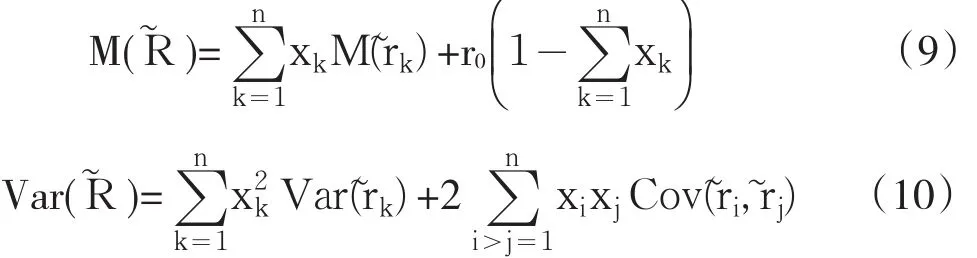
基于Markwitz的MV模型，可以建立如下的风险投资决策模型：

其中σ为风险上限(σ＞0)，μ为收益率的下限(μ＞0)，(PL1)，(PL2)为二次规划模型，可以应用Matlab,Lingo等软件编程求解。

五、实证分析

为了验证第四部分提出的模型，本节利用从基金市场选取的工银四季债券（代码164808）选取的组合来进行验证。通过RESSET金融研究数据库可知，截至2012年12月31日，该基金拥有7种债券、1种中期票据以及银行存款，7种债券代码分别为110015、110016、110018、113001、113003、118007、122079。此处，我们可以将中期票据以及银行存款一起看做是无风险投资，以5年定期存款利率作为无风险的投资利率，从而r0=5.5%。由于118007是2012年6月发行，故我们选取2012年11月到2013年10月共10多个交易日的日收益率的均值作为债券的预期收益率，其余6种债券选取从2012年6月到2013年10月共200多个交易日的日收益率的均值作为债券的预期收益率。由于债券价格同一天也是波动的，故选取三角模糊数作为债券每天的收益率，用oit、cit、lit、hit分别表示债券i在第t个交易日的开盘价、收盘价、最低价和最高价，表示债券i在第t个交易日的收益率，设其中

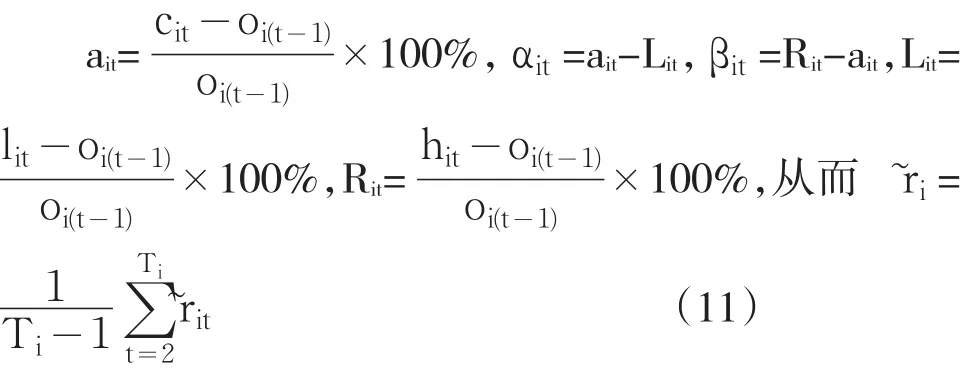
其中Ti是债券i的交易天数。

由于将收益率看作三角模糊数，故模型(PL1) (PL2)可以转换成如下形式：

用上述方法可求得7种债券的预期收益率及可能性均值见表1。

表1 7种债券的模糊收益率及可能性均值

若每种债券的投资下限分别取0.2、0.02、0.01、0.2、0.01、0.1、0.1，投资上限分别取0.3、0.03、0.02、0.4、0.02、0.2、0.2，则对于不同的σ值(TPL1)的最优解见表2。

由表2可以看出，随着风险上限的提高收益率随之增加，当承受的风险上限为0.007时，此时可将总资金的16.89%投入122079（11上港02），110015（石化转债）、113001（中行转债）、118007（12威信债）均投入总资金的20%，110016（川投转债）投入总资金的2%，110018（国电转债）、113003（重工转债）均投入总资金的1%，而剩余的资金投入无风险组合。而当承受的风险上限为0.01时，此时可将总资金的25.16%投入113001（中行转债），110015（石化转债）、118007（12威信债）、122079（11上港02）均投入总资金的20%，3%投入110016（川投转债），110018（国电转债）、113003（重工转债）均投入总资金的2%，剩余资金投入无风险组合。当承受的风险上限大于等于0.0118时，投资组合的比例不再发生变化，此时该组合能获得的最大收益为16.25%。

表2 对应于不同风险上限的组合投资模型的投资比例及收益

若每种股票的投资下限仍取0.2、0.02、0.01、0.2、0.01、0.1、0.1，投资上限仍分别取0.3、0.03、0.02、0.4、0.02、0.2、0.2，则对于不同的μ值(TPL2)的最优解见表3。

表3 对应于不同收益下限的组合投资模型的投资比例及风险

由表3可以看出，随着收益下限的提高风险也随之增加，当期望收益率下限为0.1时，可将总资金的2%投入110016（川投转债），110015（石化转债）、113001（中行转债）均投入总资金的20%，110018（国电转债）、113003（重工转债）均投入总资金的1%，118007（12威信债）、122079（11上港02）均投入总资金的10%，而剩余的资金投入无风险组合，此时承受的风险为0.6%。而当期望收益率下限为0.25时，投入这7种债券的资金比例分别23.49%、2%、1.16%、28.57%、1.23%、10.15%、13.06%，剩余资金投入无风险组合，此时承受的风险为12.06%。工银四季债券（代码164808）截至2012年12月31日投资的各种组合占债券组合的市值比例见表4。

表4 164808投资的各种组合占债券组合的市值比例

通过表2、表3及表4的数据分析可以看出，该基金投资的各种债券组合的比例与表3的数据相对应，属于风险规避型。同时也表明，第四部分建立的模型在实际的市场投资中也具有一定的指导意义。

六、结论

本文建立了一种存在无风险证券的投资组合选择模型，但与传统的投资组合模型不同。由于资产收益是波动的，将资产的收益率看做是模糊变量，分别将可能性均值、可能性方差看做风险资产的收益与风险的度量。根据传统的MV模型的思想，建立了一种基于模糊变量的投资组合选择模型，再利用模糊决策的相关理论，将模型求解问题转化为二次规划或线性规划问题，从而可以使用Matlab,Lingo等软件求解。最后通过实证分析来表明该模型对实际市场的投资具有一定的指导意义，不同风险偏好的投资者可以根据自己的风险偏好以及能够承担的风险和期望的收益来进行选择投资。

[1]Markowitz H.Portfolio Selection[J].Journal of Finace,1952,（7）:77-91.

[2]Sharp,WF.Portfolio Theory and Capital Markets [J].Journalof Finace,1972,27（4）:968-969.

[3]Robert CMerton An Analytic Derivation of the Efficient Portfolio Frontier[J].The Journal of Financial and Quantitative Analysis，1972,7（4）：1851-1872.

[4]Pang,Jong-Shi.A New and Efficient Algorithm for a Class of Portfolio Selection Problems[J].OperationsResearch.1980,28（3）:754-767.

[5]Markowitz H.Portfolio Selection:Efficient Diversification of Investments[M].New York:Wiley.

[6]李洪兴，汪培庄.模糊数学[M].北京：国防工业出版社，1994.

（责任编辑：张艳峰）

1003-4625（2014）08-0001-04

F830.91

A

2014-06-04

本文为国家社科基金青年项目(编号13CRK027)，潍坊市科技发展资助项目（201201112）。

隋云云（1981-），女，山东龙口人，辽宁大学经济学院博士研究生，讲师，研究方向：经济统计，模糊数学，组合投资理论与计量经济模型；马树才（1945-），男，辽宁岫岩人，教授，博导，研究方向：计量经济模型及方法。