复杂表面问题的有限元计算与分析
华沛
(河南城建学院,河南 平顶山 467000)
复杂表面问题的有限元计算与分析
华沛
(河南城建学院,河南 平顶山 467000)
本文主要通过对复杂接触表面问题、流固耦合方程组以及边界条件切触不确定性的分析详细探讨了复杂表面问题的有限元计算的问题,希望能够对我国科研测试中的碰撞安全测试的最优接触问题的计算方法的研究有所帮助.
复杂接触表面;流固耦合方程组;边界条件切触不确定性;有限元
近年来,随着我国经济的高速发展,我国的在科学技术领域的研究越来越精确.有限元算法(FEA)在科研测试中也开始变得越来月重要.就目前来看,有限元计算法在接触表面问题的数值计算中开始获得较大的应用,其中较为典型就是在三维立方元模型高性能前处理计算中应用.三维立方元模型的计算以算法作为分类的标准,主要可以分为隐式以及显式,其中隐式算法主要就是要对立方程组的联解,在数学研究上来看,也即是应该拉格朗日乘子法,且会在计算中常有难以收敛的情况发生,改重算法的优点在于能够对表面接触节点边界条件有着精确的计算.对于显式算法来说.在计算中有点是不需要对联立方程求解,缺点在于受稳定性限制.总之,就目前对复杂表面问题的有限元计算分析来看,立方元相关的计算是主要的研究方向,同时也是力学与经济学相关领域的随机模型重要的参考对象.
1 复杂接触表面问题
对于复杂接触表面问题主要可以从两个方面进行研究分析,也即是从确定性模型之上的随机边界条件分析以及蜂窝多孔复合材料的应用和算法结果,下面对此进行简单的分析探讨:
1.1 确定性模型之上的随机边界条件分析
确定性模型之上的随机边界条件分析,主要可以分为三个步骤,第一步就是对于涉及时间变量的初边值问题的分析,对与时间变量初边值的处理基本就是依靠有限元方法求解的基本思想,也就是分开处理涉及到的时间变量以及与空间变量,使用有限元法的离散化对空间变量进行处理计算,从而得到与初值相关的常微分方程组.第二步骤,对第一步骤中有关的时间变量的处理,对于时间变量的处理是不同于空间变量的,时间变量的处理主要是应用差分方法的离散化,从而得到线性代数方程组.第三步,利用确定性模型的工程试验相关的数据库,综合第一步和第二步所得的时间和空间相关变量的初边值可以确定离散系统随机初边值条件,进而对该离散系统进行数学化的运算,从而能够取得相应研究对象,比如像应力、塑性变形率以及常见的碰撞加速度控制等等相关的各种分布函数的高精度解.图1即为碰撞研究对象中应力(VMS)与碰撞角度(IA)的联合分布频率函数的图解.

图1 应力(VMS)与碰撞角度(IA)的联合分布频率随时间的变化
1.2 蜂窝多孔复合材料的应用和算法结果
关于有限元计算方法在蜂窝多孔复合材料(如图2所示的力学结构图)这种典型复杂表面问题中应用计算来说,重要的问题是对动力方程中相关的多尺度算法的计算规模的考虑,主要方法那就是在蜂窝多孔材料区域耦合方程中,关于对时间变量的处理时,加强对积分变换的应用,同时对带有参数关于蜂窝多孔材料的新耦合方程进行合理的多尺度分析,以求得简单易于计算多尺度算法.不仅如此,在对蜂窝夹层结构的表面问题进行计算时,可以应用三维网格进行数值进行计算,以达到对蜂窝多孔复合材料表面问题对有限元的应用,从而求出结果的目地.
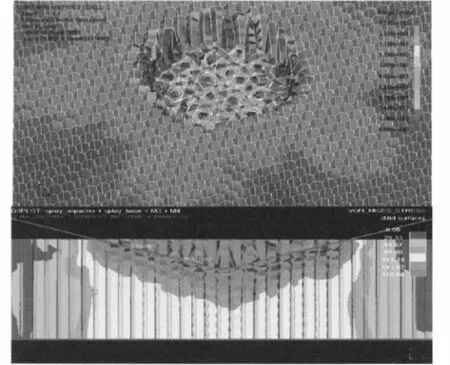
图2 蜂窝多孔复合材料区域上耦合弹塑性方程的算法结果
2 流固耦合方程组
在复杂表面问题的有限元计算中,流固耦合方程组也是整个计算中重要的环节,流固耦合方程组是对复杂表面性质的描述的基础,也是计算的方法之一,下面就从流固耦合方程组的离散系统和复杂接触表面的计算方法这两方面进行简单分析:
2.1 流固耦合方程组
流固耦合方程组对于复杂接触表面问题的来说,主要是起到媒介的作用,也就是可以通过流固耦合方程组进行描述的同时,还能够通过流固耦合方程组进行计算,换从研究的角度来说,主要是表现在下面的两个方面:在工程材料科学中的相关标准变量的基础之上,以对非牛顿P-T/T方程所表现的处理特性为切入点,分析复杂接触表面的外延以及简单剪切速率的阻力;以Cauchy守恒方程为基础,通过对方程的计算可以得出,由于宏观与微观应力场中因素τ分布的变化,产生的弹塑性材料大变形的基本情况,也即是研究中通常所说的切变致稀),其中关于移动边界层在时间点数值结果如图3所示.

图3 三维碰撞模型中接触表面移动边界层,部分时间节点上的结果
2.2 复杂接触表面的计算方法
通过上文对复杂接触表面的基本情况以及性质的分析可以得知,在对复杂表面问题处理是可以以非牛顿耦合方程模型为基础进行探究,具体是可以通过非牛顿耦合方程模型随机边界层的特点来分析研究,在此研究为基础,对相关研究的任意元素的计算进行数值仿真.具体的来说也就是应用人工边界法数值来求解非线性外问题,从而达到对复杂接触表面年的计算.但是,该种计算方法应该注意的是,人工边界法数值求解非线性外问题,其基础是在得到人工边界上相对于该非线性问题相关的准确近似的边界条件.该边界条件一般来说就是未知函数及其微商相对于与计算相关的人工边界的非线性积分方程.
3 边界条件切触不确定性
对于复杂接触表面处理的有限元的计算与分析中,边界条件切触的不确定性也是整个计算中的重点难点,下面就从边界条件切触不确定性的边界层特征函数和边界层的外解渐进分析以及内解渐进分析进行阐述:
边界层的特征函数.在复杂表面问题中利用边界层理论对有限元接触边界相关的非线性特征函数基进行探讨,这是对复杂表面问题进行有限元计算的关键点之一.简单的来说也即是以边界层外解与内解逼近为基础,通过对非线性边界条件的匹配方法.从而得到跳跃条件特征值谱P与参数R,G,N及χ的关系,也即是得到了复杂表面有限元后处理的优化基函数
外解的渐近分析.边界条件切触性对于渐近分析,主要就是针对对外解问题微分方程(方程一)而言,通过该方程的分析,可得到相关的弹性方程以及耦合方程组在复杂接触表面层厚中当δ→0时,将会丧失方程或方程组的椭圆性,这也即是要求构造新的空间,去讨论光滑解相关的收敛性.因此,就外解的渐近分析来说,边界层外稳态约束场是好的逼近.方程如下:
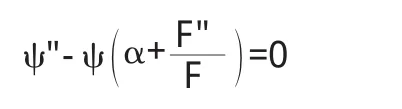
内解的渐近分析.对于内解的渐近分析,主要是对边界层内解的进行计算,也即是通过对非线性相关的耦合程进行线性变换,同时对傅立叶进行调和分析,在进新的参数的情况下,将边界相关的三维流体动力学方程转换为一维复空间的阶微分方程,方程如下:
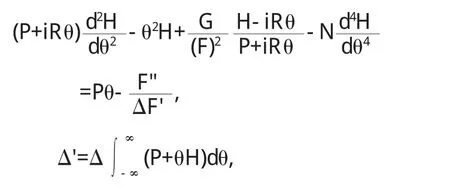
通过对方程的分析与计算,从而可以确定复杂接触表面的非线性有限元特征函数基,进而能够保证在复杂表面有限元相关计算中的的稳定与收敛.
总而言之,在对复杂表面问题的有限元计算与分析时,计算的方法和基础就在于去采用流固耦合非牛顿流体方程,使用该方程对复杂表面的初边值求解三维层结构特性,同时可以利用变分原理的摄动问题的有限元方法,在已经研发使用的高性能软件平台对所得数据实现挖掘处理,进而得到有效的结果.此外,复杂接触表面的有限元计算,还可以利用基于渐近摄动方法,已经较为成熟边界层理论进行研究,从而得到可解的微分方程特征的函数空间,这也可以用来优化有限元基函数的解,达到对复杂表面问题有限元计算的目地.
〔1〕林群,周俊明,陈竤焘.椭圆形方程四面体线元的超逼近与外推[J].数学实践与认识,2009,39(15):200-208.
〔2〕林群,谢和虎,罗福生,等.Stokes方程非协调混合元的特征值下界[J].数学的实践与认识,2010,40(19):157-168.
〔3〕李开泰,黄爱香,黄庆怀.有限元方法及其应用[M].北京:科学出版社,2005.
O241.82
A
1673-260X(2014)03-0006-02

