一种基于Hilbert-Huang 变换和ARM A 模型的时间序列预测方法

马亮亮

（攀枝花学院数学与计算机学院，四川攀枝花617000）

一种基于Hilbert-Huang 变换和ARM A 模型的时间序列预测方法

马亮亮

（攀枝花学院数学与计算机学院，四川攀枝花617000）

提出了一种基于Hilbert-Huang变换和ARMA模型的时间序列预测方法。采用Hilbert-Huang变换将原时间序列分解成若干个平稳的固有模态函数分量，求出每一个固有模态函数分量的瞬时频率和瞬时幅值，然后对每一个固有模态函数分量的瞬时频率和瞬时幅值序列建立ARMA模型，最后通过合成得到原时间序列的ARMA预测模型。实验结果表明，此方法可有效地应用于非平稳时间序列的预测。

Hilbert-Huang变换；ARMA模型；瞬时频率；瞬时幅值；固有模态函数

0 引言

长期以来非平稳时间序列囿于理论的发展，只能转化为平稳的时间序列来处理。近年来，随着短时Fourier变换（Short Time Fourier Trans⁃form，STFT）［1］、W igner-Ville分布［2］、小波分析等［1-3］新方法的出现，人们对于非平稳时间序列的认识和研究取得了较大的成就。短时Fourier变换依赖于传统的Fourier谱分析，操作时需假设待分析的数据是分段平稳的；W igner-Ville分布则改进和优化了短时Fourier变换的部分缺点和性能；小波分析是目前比较流行的非平稳时间序列分析方法［4］。

ARMA模型是一种新型的时间序列分析方法，能比较深刻和集中地表达动态系统的客观规律。但是，ARMA模型只适用于平稳时间序列的分析，而实际中的时间序列本质上是非平稳的，因此，直接采用ARMA模型对动态系统的客观规律进行分析效果不佳。如果采用非线性ARMA预测模型（如时变参数NARMA等模型），则会导致计算量显著增加［5-6］。

Hilbert-Huang变换是由Huang等［7］提出的一种较新的非平稳时间序列分析方法。该方法兼容了小波分析的所有优点，在分辨率上消除了小波分析的模糊性和不清晰性，且有更准确的谱结构。Hilbert-Huang变换的算法分析过程为：首先采用经验模式分解（EmpiricalMode Decomposi⁃tion，EMD）方法将非平稳的时间序列分解为若干个固有模态函数（Intrinsic Mode Function，IMF）之和，然后再对各个固有模态函数（IMF）分量进行Hilbert变换，得到各个固有模态函数分量的瞬时频率和瞬时幅值，最后将瞬时频率和瞬时幅值组合得到原序列完整的Hilbert谱。由于固有模态函数分量的瞬时频率和瞬时幅值均是平稳的时间序列，且包含了原序列的所有信息，因此，通过对这些瞬时频率和瞬时幅值序列进行分析可有效提取原序列的信息［8］。本文在Hilbert变换的基础上，对各个固有模态函数分量的瞬时频率和瞬时幅值序列分别建立ARMA模型，并以此对研究对象进行分析。

1 Hilbert-Huang变换［7，9］

Hilbert-Huang变换包括经验模式分解和Hil⁃bert变换两个部分，其中经验模式分解是其核心部分。

1.1 经验模式分解

假设所研究的时间序列由简单的固有模态函数组成，将原时间序列分解为一系列表征时间尺度的固有模态函数分量，此过程也称为筛选过程（The Shifting Processing）［4］。

对于给定的原时间序列y(t)，其筛选过程如下：

1）分别找出原序列y(t)的所有极大值点和极小值点，然后拟合序列的上、下包络线ymax(t)和ymin(t)，并计算其平均值x1(t)：

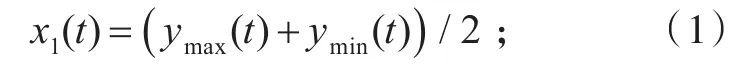
2）用y(t)减去x1(t)得到z1(t)，将z1(t)视为新的y(t)，重复上述步骤；

3）重复k次直到均值趋于0，此时所得z1k(t)符合固有模态函数的定义要求，便得到了第1个固有模态函数分量c1(t)；

4）从原时间序列中减去c1(t)，得到

5）将r1(t)作为原时间序列，重复步骤1）至4），得到第2个固有模态函数分量c2(t)，重复n次，得到n个固有模态函数分量。

最终原时间序列可表示为

1.2 Hilbert变换

经验模式分解将原时间序列自适应地分解为若干个固有模态函数分量之和，使瞬时频率具有物理意义。因此可以通过Hilbert变换计算出每个固有模态函数分量的瞬时频率和瞬时幅值。

对（3）式中的ci(t)(i=1，2，…，n)分别进行Hilbert变换

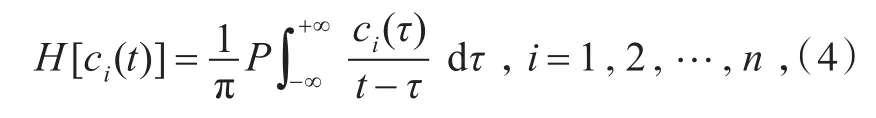
其中P为柯西主值。

由ci(t)和H[ci(t)]构造解析序列时变幅值ai(t)的时频分布定义为分量ci(t)的Hil⁃bert谱，记为

2 基于Hilbert-Huang变换和ARM A模型的时间序列预测方法

假设采用经验模式分解方法对原时间序列进行分解得到了n个固有模态函数分量ci(t) (i=1，2，…，n)，对所有的固有模态函数分量进行Hilbert变换后得到瞬时频率fi(t)(i=1，2，…，n)和瞬时幅值ai(t)(i=1，2，…，n)，其中fi(t)和ai(t)分别表示第i个固有模态函数分量ci(t)的瞬时频率和瞬时幅值。这样，通过Hilbert-Huang变换，原时间序列y(t)的信息就完全可以由这些瞬时频率和瞬时幅值来刻画，因此通过提取所有瞬时频率fi(t)和瞬时幅值ai(t)的信息，可以得到原时间序列y(t)的信息。

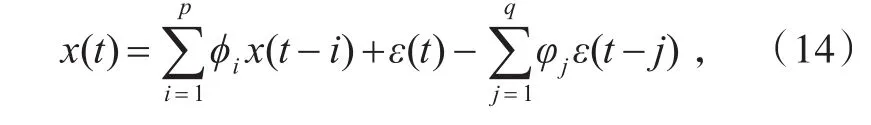
对任意的平稳时间序列x(t)建立如下的自回归移动平均模型ARMA(p，q)［10-13］其中φi(i=1，2，…，p)、φj(j=1，2，…，q)分别是序列x(t)的自回归模型AR(p)和移动平均模型MA(q)的模型参数；ε(t)是模型的残差，是均值为零、方差为σ2的白噪声序列。

基于Hilbert-Huang变换和ARMA模型的时间序列预测方法如下：

1）对原时间序列y(t)进行经验模式分解，假设得到n个固有模态函数分量ci(t)(i=1，2，…，n)；

2）由式（4）～（9）求出每一个固有模态函数分量ci(t)的瞬时频率序列fi(t)和瞬时幅值序列ai(t)；

3）为消除原时间序列的幅值对模型残差方差的影响，对fi(t)和ai(t)分别进行归一化处理，得到新的时间序列f^i(t)和a^i(t)：

其中φ^i和φ^j分别为模型的预测参数值。

3 应用

原时间序列数据取自青海海西州第一人民医院的糖尿病发病率，对应的时间序列图如图1所示。其中横坐标表示2001年1月至2007年12月的84个月份数据，纵坐标表示糖尿病发病率（百分比）。从图1可以看出，原发病率数据y(t)的均值、相关函数随着时间的改变而上下剧烈振动，是非平稳的时间序列。

图1 糖尿病发病率时间序列图Fig.1 Tim e seriesof diabetes incidence rate

将原发病率数据分为两个部分，用2001年1月至2006年12月的前72个数据来预测2007年1月至12月的后12个数据。采用经验模式分解方法对原序列进行分解，得到1个固有模态函数分量c1(t)和1个残余函数r1(t)。对固有模态函数分量c1(t)进行Hilbert变换，得到瞬时频率和瞬时幅值（见图2）。

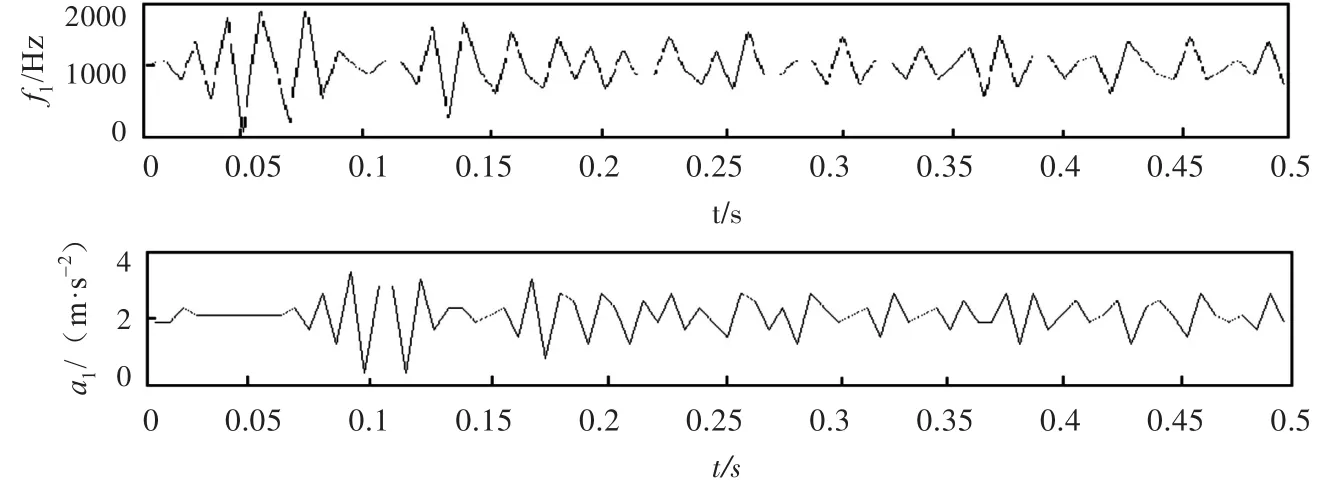
图2 固有模态函数分量的瞬时频率和瞬时幅值Fig.2 Inslantaneous frequency and am p litude for intrinsicm ode function com ponent

对瞬时频率f1(t)和瞬时幅值a1(t)进行归一化处理，得到f1^(t)和a^1(t)。对序列f1^(t)和a^1(t)分别建立ARMA模型：

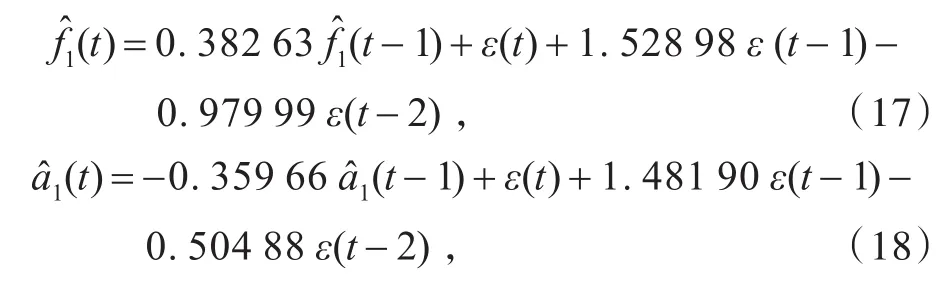
合成f^i(t)和a^i(t)，便得到原时间序列y(t)的预测模型：

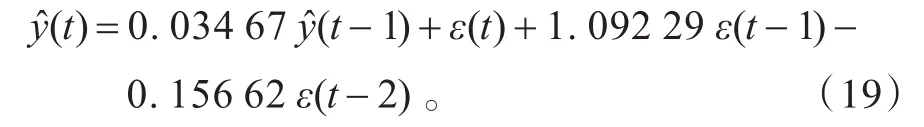
利用（19）式对2007年1月至12月的测试数据进行预测检验，结果如图3所示。从图3可以清楚地看出，模型的预测值与实际的糖尿病发病率值很接近（除极少数点外），变换趋势基本吻合，且整体的预测精度较高，表明本文所建立的基于Hilbert-Huang变换和ARMA模型的时间序列预测方法是正确、合理的。

4 结语

对于非平稳时间序列，本文提出了基于Hil⁃bert-Huang变换和ARMA模型的时间序列预测方法。该方法在对原非平稳数据建立ARMA模型之前，先采用Hilbert-Huang变换对原时间序列进行预处理，得到瞬时频率和瞬时幅值均是平稳的时间序列（它们包含了原时间序列的最主要信息），然后对每个瞬时频率和瞬时幅值序列分别建立ARMA模型，最后通过合成得到原时间序列的ARMA预测模型。通过对实验数据的分析，所得预测结果与真实值基本吻合，预测精度较高，验证了本文提出的方法能够应用于非平稳时间序列的预测。

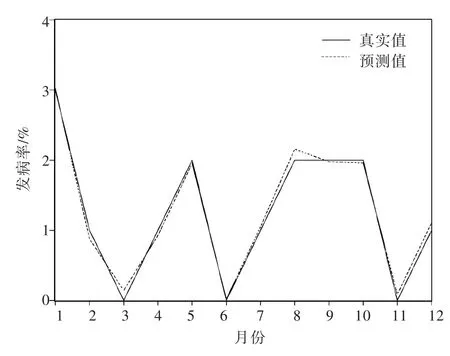
图3 糖尿病发病率预测值Fig.3 Pred iction value of diabetes incidence rate

［1］张贤达.现代信号处理［M］.北京：清华大学出版社，1995.

［2］COHEN L.时频分析：理论与应用［M］.白居宪，译.西安：西安交通大学出版社，1998：50-65.

［3］李建平.小波分析与信号处理——理论、应用及软件实现［M］.重庆：重庆大学出版社，1997.

［4］王海涛，宋艺.基于Hilbert-Huang变换的非平稳随机信号处理［J］.网络与信息，2009，23（7）：17-18.

［5］程军圣，于德介，杨宇.一种基于Hilbert-Huang变换和AR模型的滚动轴承故障诊断方法［J］.系统工程理论与实践，2004，24（10）：92-97.

［6］王文华，王宏禹.一种非平稳随机信号模型的时变参数估计算法性能研究［J］.大连理工大学学报，1997，37（1）：97-102.

［7］HUANG N E，SHEN Z，LONG S R.The empirical mode decomposition and the Hilbert spectrum for non⁃linear and non-stationary time series analysis［J］.Pro⁃ceedings of The Royal Society A：Mathematical，Physi⁃caland Engineering Sciences，1998，454：903-995.

［8］程军圣，于德介，杨宇.基于支持矢量回归机的Hil⁃bert-Huang变换端点效应问题的处理方法［J］.机械工程学报，2006，42（4）：23-31.

［9］HUANGN E，SHEN Z，LONG SR.A new view ofnon⁃linear water waves：The Hilbert spectrum［J］.Annu Rev Fluid Mech，1999，31：417-457.

［10］马亮亮.基于因子BP神经网络预测模型的胃溃疡发病率预测［J］.北京联合大学学报：自然科学版，2012，26（3）：73-76.

［11］马亮亮.基于粗糙集和RBF神经网络的脑梗塞发病率预测［J］.西北民族大学学报：自然科学版，2012，33（3）：17-21.

［12］马亮亮.基于PCA-ARIMA模型的高血压发病率预测［J］.河北北方学院学报：自然科学版，2013，29（2）：26-29.

［13］易丹辉.数据分析与EViews应用［M］.北京：中国统计出版社，2005.

A Prediction M ethod for Tim e Series Based on Hilbert-Huang Transform and ARM A M odel

MA Liang-liang
（College ofMathematicsand Computer，Panzhihua University，Panzhihua 617000，Sichuan，China）

A prediction method for time series based on Hilbert-Huang transform and ARMA model is proposed.The Hilbert-Huang transform is used to decompose the original time series into a number of intrinsic mode function components and the instantaneous frequencies and amplitudes of each intrinsic mode function component are obtained.Then the ARMA model of each instantaneous frequency and amplitude sequence is established.Finally，ARMA prediction model of the original sequence is obtained through compounding.Experimental examples demonstrate that the method based on Hilbert-Huang transform and ARMA model can be applied to predict non-stationary time series effectively.

Hilbert-Huang transform；ARMA model；instantaneous frequency；instanta⁃neousamplitude；intrinsicmode function

O29

A

1673-0143（2014）01-0028-04

（责任编辑：强士端）

2013-06-28

国家自然科学基金资助项目（60673192）；四川省科技厅资助项目（2013JY0125）；攀枝花学院校级培育项目（2012PY08）；攀枝花学院校级科研项目（2012YB21）；攀枝花学院院级科研创新项目（Y2013-04）

马亮亮（1986—），男，讲师，硕士，研究方向：数学模型和模型优化。