H∞与滑模融合控制算法在磁悬浮系统中的应用

李丹丹，何荣卜，张彩红

1.六盘水师范学院矿业工程系，贵州六盘水 553004

2.六盘水供电局城区供电分局，贵州六盘水 553004

H∞与滑模融合控制算法在磁悬浮系统中的应用

李丹丹1，何荣卜2，张彩红1

1.六盘水师范学院矿业工程系，贵州六盘水 553004

2.六盘水供电局城区供电分局，贵州六盘水 553004

磁悬浮系统在实际运行中会出现模型摄动和各种外界干扰，提高磁悬浮系统的鲁棒性非常重要，给出了磁悬浮系统的数学模型；结合H∞控制和滑模控制的优点，给出一种H∞控制和滑模控制的融合算法，把该算法应用在磁悬浮系统中；通过Matlab仿真，验证了该算法能有效抑制磁悬浮系统中存在的确定性和不确定性干扰，从而使控制系统的性能得到提高。

磁悬浮；积分滑模；鲁棒；H∞控制

1 引言

磁悬浮技术在交通、冶金、机械、电器、材料等方面有广阔应用前景。其中最为重要的应用有磁悬浮列车、磁悬浮轴承、高速磁悬浮电机、磁悬浮鼓风机、磁悬浮潜水电泵。磁悬浮控制系统要求其在运行过程中必需能够在种种不确定因素下仍能保持较好的性能，所以对磁浮系统设计鲁棒性较好的控制器非常必要。滑模变结构控制作为一种鲁棒控制方法，仅仅对满足匹配条件的内部参数摄动和外部扰动具有良好的鲁棒性限制了该方法在实际方面的应用[1-2]。因而要克服系统中的非匹配不确定性，必须结合其他的控制方法构造具有鲁棒性的滑模控制系统，文献[3]将系统中的不确定性转化为LMI约束条件，进而设计滑模面，一旦系统状态到达滑模面，就能实现对不确定性的不变性，但是这种方法只能解决一部分非匹配不确定性问题，并且对不确定性的限制也比较苛刻。文献[4]提出了一种自调整的切换控制算法，该算法在某种程度上改善了滑模控制器的不足，但是上述相当一部分控制策略其算法复杂、动态性能较差，这与滑模变结构控制简单、灵活的特点并不一致。这些不足通常使得在实际应用中遇到很大的困难。在文献[5]中给出了一个很好的控制器设计策略：把积分滑模控制和鲁棒控制结合在一起可以有效地保证系统在不匹配不确定下仍然稳定。所以本文应用这种设计思想，设计了磁悬浮系统的H∞和积分滑模融合控制器。该控制器由两部分组成：积分滑模控制器和H∞控制器。由于积分滑模控制作用的引入，匹配器由不确定性被完全抵消，剩下的非匹配不确定性由H∞控制器进行处理。从而即能保证闭环系统具有良好的稳定性，同时又能满足一定的H∞性能指标，实现系统的优化控制，最后通过仿真验证了所提算法的有效性。

2 磁悬浮系统数学模型建立

单自由度磁悬浮系统是研究磁悬浮技术很好的平台，它主要有铁芯、线圈、光电源、位置传感器、放大及补偿装置、数字控制器和控制对象钢球等元件组成，系统的构成如图1所示。

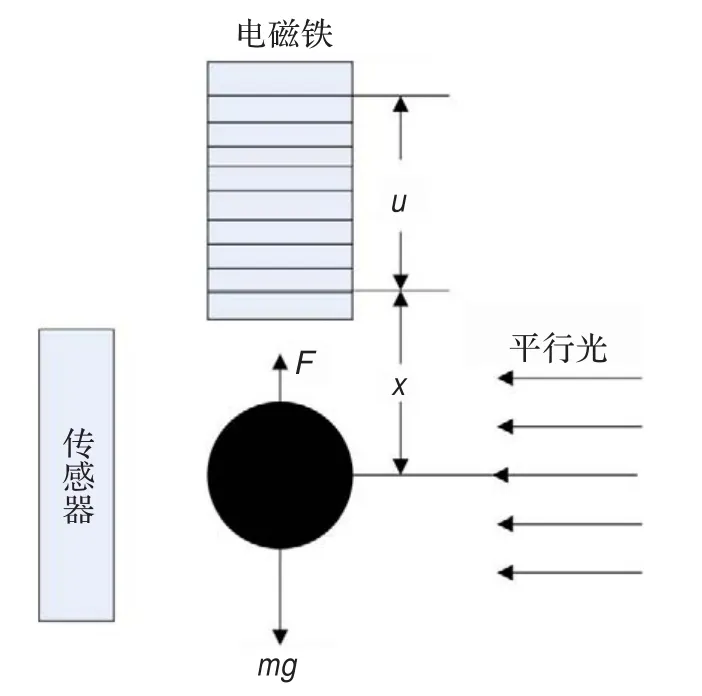
图1 磁悬浮控制系统构成

磁悬浮系统的动力学平衡方程为：

其中，F(x,i)=-N2μ0si(t)2/4x2(t)，μ0=4π×107(H/m)；s(m2)为铁芯的极面积；N为电磁铁线圈匝数；x(m)为小球质心到电磁铁磁极表面的瞬时气隙；i(A)为电磁铁绕组中的瞬时电流。

磁悬浮系统的电磁学方程为：

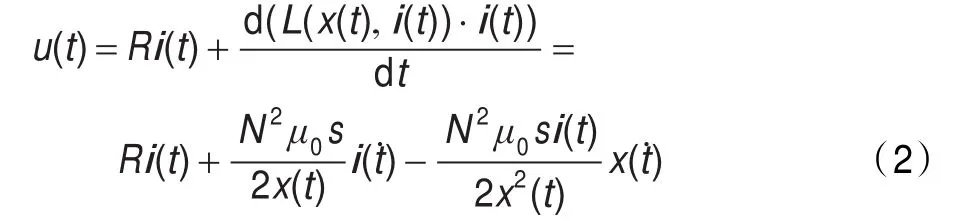
其中，L(x(t),i(t))=N2μ0s/2i(t)；R(Ω)为电磁铁的等效电阻。

考虑系统中的不确定性因素，取状态变量[x1x2x3]= [x x˙i]系统非线性状态方程为：

应用泰勒级数展开的方法得到磁悬浮系统的线性化模型为[6]：

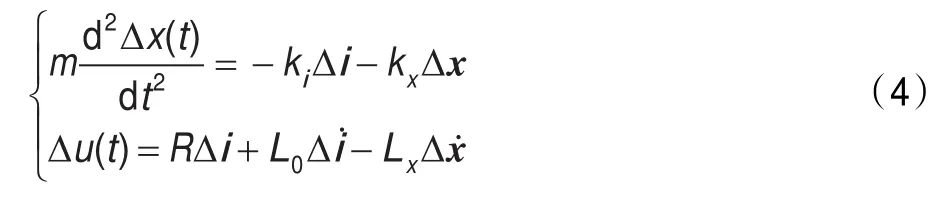
若取状态变量为：Δx=x-x0;Δx˙=x˙;Δi=i-i0；[x1x2x3]=[Δx Δx˙Δi]，可得系统线性化的状态方程为：

3 控制器的设计

为便于分析，可把磁悬浮系统的状态方程（5）写成标称系统的形式[8]：

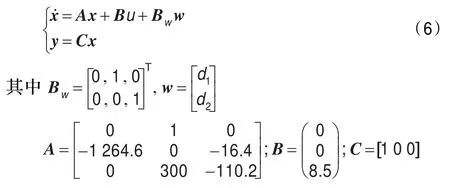
在这里，w中包含了系统匹配的不确定性和不匹配的不确定性，在控制器设计之前，先对系统的不确定性进行分解，分别表示出它的匹配不确定性和非匹配不确定性，首先引入如下的定义。

定义1（单位矩阵）[6]定义一个特殊的单位矩阵I1= BB++B⊥B⊥+，其中，B+定义为B的左逆矩阵，B+= (BTB)-1BT，定义B⊥∈R3×2，且B+B⊥=0，I1∈R3×3。

然后，根据定义1，可以对式（6）引入如下的矩阵：

设控制律u(t)=u0(t)+u1(t)[9]，其中控制器u0(t)设计用来保证标称系统的性能，是通过积分滑模控制的思想得到的；不连续的控制u1(t)是为了保证系统状态能进入滑模面来消除系统匹配的不确定性，是通过H∞控制的思想得到的。设滑模面函数为：

其中，G∈Rm×n是要设计的矩阵，需保证GB可逆。为了得到滑模面上的滑动模态方程，采用等效控制的方法[10]，对式（7）求导得：

其中，ρ是确保闭环系统状态变量能够进入滑模面的增益系数。

从系统等效滑动模态方程（9）可以看出，经过积分滑模控制器的设计，系统匹配的不确定项dm已经被消除，等效不确定项deq中只含有非匹配的不确定项，它的矩阵系数N=[I-B(GB)-1G]的选取是接下来设计的重点，N的选取主要影响以下两方面问题：

（1）会不会有一个N*，能让等效不确定项deq的范数最小。

（2）N*的选取会不会让等效不确定项放大，即||deq||是否会大于||du||。

经过证明可以得到G=B+能使deq的范数最小且能保证矩阵N*不会放大非匹配不确定项[12]。因此本文在接下来的设计中选择G=B+，此时可以得到：

下面给出u0(t)的设计过程。

引理1对于系统式（6）和性能指标（1）和（2）存在一个H∞控制器，满足||TZW||∞＜γ当且仅当存在一个对称的、半正定的矩阵X满足Riccati方程：

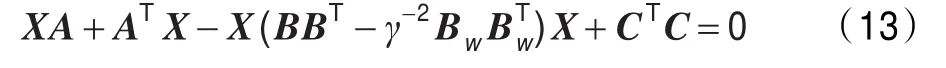
且H∞控制律为：

性能指标（1）：[A，B]是可稳定的，要求所有加权函数是稳定的；[C1，A]是可检测的，确保状态的有界性；并且[C1，D11]=[0，I]，保证评价输出z和控制量以及状态变量之间没有交叉权，且控制量的权矩阵是单位矩阵。

性能指标（2）：当初始条件x(0)=0时，从系统的外部扰动输入w到评价输出z的闭环传递函数Tzw(s)的H∞范数达到极小，也就是求控制器K使γ0=min{||Tzw(s)||∞}，若给定γ＞γ0求反馈控制器K，使闭环系统内部稳定，同时min||Tzw(s)||∞＜γ则称为H∞次优控制问题[13]。

从式（9）中可以看出，经过积分滑模控制器的设计，磁悬浮系统中匹配的不确定性已经被消除，可以保证系统状态到达理想滑动模态，所以在设计u0(t)时，系统的状态方程变为：

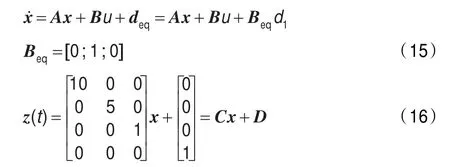
z(t)是自己构造的系统输出，矩阵C，D分别代表系统状态和输入所占权重。

通过解黎卡提方程：

可以得到磁悬浮控制系统的H∞控制器的状态反馈控制律u0(t)为：

从式（19）可以看出H∞控制器u0(t)隶属于积分滑模控制器。

因此，磁悬浮控制系统可以通过控制律式（11）、式（12）保证较好动态性能并且能对系统匹配的不确定性有较好的鲁棒性，通过控制律式（18）能增加系统对不匹配不确定项的鲁棒性，从而优化了磁悬浮系统的整体性能。磁悬浮控制系统结构如图2所示。

图2 H∞和积分滑模控制的融合控制系统结构图

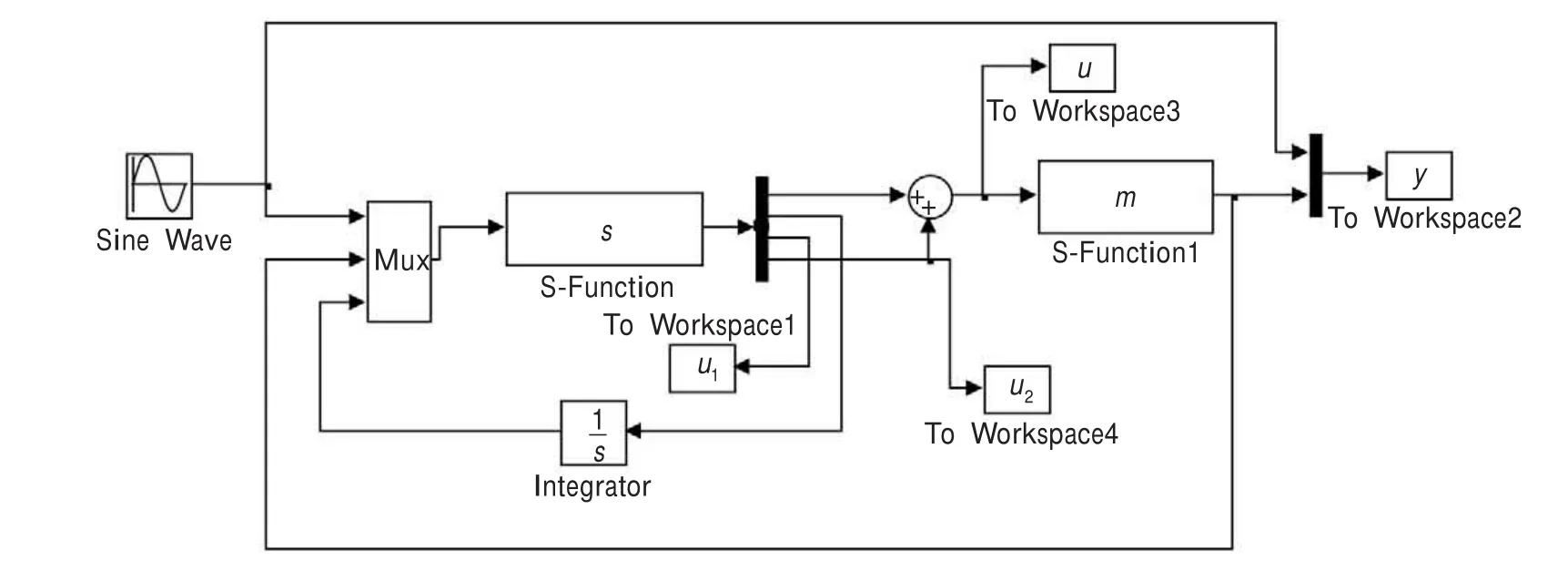
图3 H∞和积分滑模控制的融合控制系统仿真图

4 Matlab仿真

在Simulink下搭建了磁悬浮系统的仿真模型如图3所示，其中控制器部分和磁悬浮系统模型是用S函数编写[14-15]。

仿真中所用参数分别为：G=[0，0，1/8.5]，ρ=1.25，设仿真初始值为x=[0.15，1，1]T，系统的不确定性用频率为2π的正余弦信号表示，其中d1=cos(2πt)，d2= 0.5sin(2πt)。

图4是钢球位置的正弦跟踪曲线。从图中可以看出，磁悬浮系统在初始值偏离平衡位置较远的距离且存在匹配和非匹配的不确定性仍能准确跟踪位置参考值，而且系统动态响应品质较好，超调较小。

图4 位置跟踪曲线

图5是跟踪误差曲线。从图中可以看出当系统稳定后跟踪误差最大值为0.002 698，由此可以说明H∞控制和积分滑模的融合控制系统具有较好的动态跟踪性能，系统鲁棒性较强。

图5 跟踪误差曲线

为了与积分滑模控制器对比，图6与图7分别给出了磁悬浮系统积分滑模控制系统与H∞控制和积分滑模的融合控制系统的位置跟踪误差曲线。

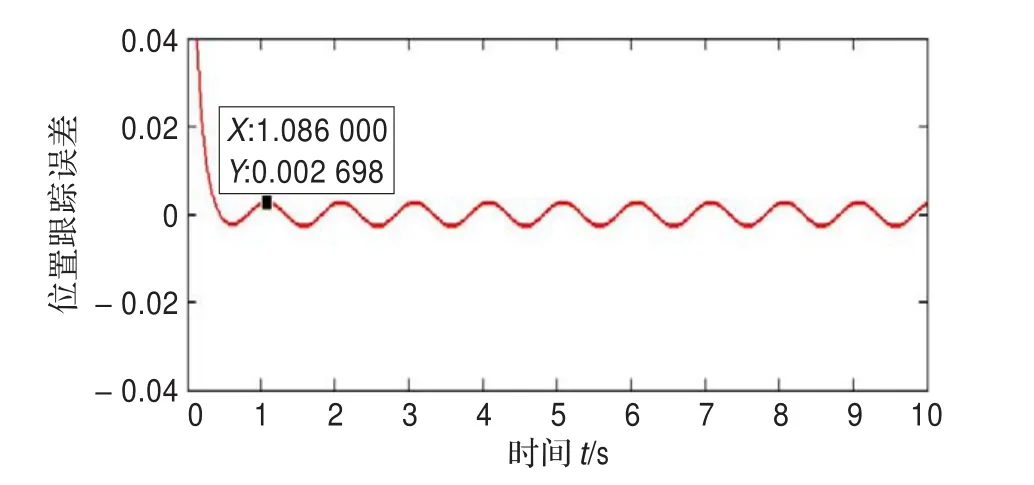
图6 积分滑模控制系统的位置跟踪误差曲线图

图7 H∞和滑模控制的融合控制系统位置跟踪误差曲线图

由图6与图7可得，H∞和积分滑模的融合控制系统的跟踪误差比单独的积分滑模控制器的跟踪误差有明显的降低，大大改善了积分传统的积分滑模控制器的性能。

5 结束语

通过图4～图7的仿真结果可以看出H∞和积分滑模控制的融合控制算法不仅能对磁悬浮系统中匹配和非匹配的不确定性具有鲁棒性，并且能保证闭环系统具有较好的动态性能，比单一的积分滑模控制系统具有更好的控制性能。

[1]Fallaha C，Kanaan H，Saad M.Real time implementation of a sliding mode regulator for current-controlled mag-netic levitation system[C]//Mediterranean Conference on Control and Automation，Cyprus，2009：696-701.

[2]Kwan C M.Sliding mode control of linear systems with mismatched uncertainties[J].IEEE Transactions on Control and System Technology，1995，31（2）：303-307.

[3]Li J.Backstepping variable structure control of nonlinear systems with unmatched uncertainties[C]//14th Triennial World Congress，Beijing，1999：67-71.

[4]Cao W J，Xu J X.Nonlinear integral-type sliding surface for both matched and unmatched uncertain system[J]. IEEE Transactions on Automatic Control，2004，49（8）：1355-1360.

[5]Fernando C，Leonid F.Analysis and design of integral sliding manifolds for systems with unmatched perturbations[J].IEEE Transactions on Automatic Control，2006，51（5）：853-858.

[6]Castanos F，Fridman L.Design of integral sliding manifolds for multi-model uncertain systems via LMI[C]// International Workshop on Variable Structure Systems，Italy，2006，12（4）：63-67.

[7]固高科技有限公司.磁悬浮系统实验指导书[M].深圳：固高科技有限公司，2005.

[8]解学生，钟宜生.H∞控制理论[M].北京：清华大学出版社，1994：82-86.

[9]Jang S，Li H S，Liu Y C.An optimal sliding-mode control approach for magnetic levitation systems[J].Asian Journal of Control，2010，12（4）：480-487.

[10]王丰尧.滑模变结构控制[M].北京：机械工业出版社，1994：45-46.

[11]Shen J C.H∞control and sliding mode control of magnetic levitation system[J].Asian Journal of Control，2002，4（3）：333-340.

[12]Luenberger D G.Optimization by vector space methods[M]. New York：Wiley，1997.

[13]Doyle J C，Glover K，Francis B A.State-space solutions toH2andH∞control problems[J].IEEE Transactions on Automatic control，1989，34（8）：831-847.

[14]刘金锟.滑模变结构控制MATLAB仿真[M].北京：清华大学出版社，2005：25-27.

[15]Chiang H K，Chen C A，Li M Y.Integral variable-structure grey control for magnetic levitation system[J].IEEE Proc Electro Power，2006，153（6）：809-814.

LI Dandan1,HE Rongbu2,ZHANG Caihong1

1.Depanrtment of Mining Engineering,Liupanshui Normal University,Liupanshui,Guizhou 553004,China
2.Liupanshui Power Supply Bureau Branch Office of Urban Area,Liupanshui,Guizhou 553004,China

Magnetic levitation control system has model perturbation and a variety of outside interference during operation, so,improving the robustness of magnetic levitation system is very important.This paper gives a mathematical model of magnetic levitation system;a fusion algorithm ofH∞and sliding-mode control is discussed;simulation is obtained by Matlab tool.The results show that the algorithm is robust to the uncertainty of the system on the matching and non-matching at the same time.

magnetic levitation;sliding mode control;robust;H∞

A

TP273+.3

10.3778/j.issn.1002-8331.1305-0198

LI Dandan,HE Rongbu,ZHANG Caihong.Fusion algorithm ofH∞and sliding-mode control for magnetic levitation systems.Computer Engineering and Applications,2014,50（6）：230-234.

六盘水师范学院采矿工程特色专业建设点（No.LPSSYtszy201101）。

李丹丹（1989—），女，助教，研究领域：鲁棒控制，非线性控制，煤矿机械故障诊断技术。E-mail：lidandande163@163.com

2013-05-16

2013-08-14

1002-8331（2014）06-0230-05

CNKI网络优先出版：2013-09-17，http://www.cnki.net/kcms/detail/11.2127.TP.20130917.1058.013.html