改进蚁群算法对车辆配送二次调度的Matlab实现*

□ 李 冲 □ 钱 静

江南大学 机械工程学院 江苏无锡 214122

带时间窗动态车辆路径问题 WTVRP（Vehicle RoutingOptimizationProblemwithTimeWindows）是指一定数量的工位点，各自需求不同数量的货物量，配送中心统一向工位点提供货物，通过安排一定顺序的行驶路线，使工位点在满足一定约束条件下，实现诸如路径最短、成本值最小、耗费时间最少等目标。路线安排过程中，根据工位点需求、车辆、运输网络等信息是否确定，WTVRP可以分为静态车辆路径问题SVRP（StaticVehicleRoutingOptimizationProblem）和动态车辆路径问题DVRP （DymamicVehicleRouting OptimizationProblem）［1］。 其中 DVRP 又包括了工位点需求 VRP、动态车辆 VRP和动态运输网络 VRP［2-4］。本文主要研究带时间窗的动态车辆VRP。

车辆配送过程中造成动态性主要由于两个原因：①现有车辆总载荷小于货物运输总量，为了完成配送任务，同一辆车在满足时间窗的条件下可能需要进行多次指派；②配送过程中车辆出现故障，需要重新派出车辆替换故障车辆［5］。此外，当前对蚁群算法的研究，大部分都暗含了现有车辆总载荷大于全部运输物料重量这个假设，而在实际生产中，工位配送总需求大于现有车辆载重总和的情况常会发生。考虑到运输成本，通常希望完成任务车辆数尽可能少，因此需考虑对部分车辆进行多次配送指派。

本文通过改进基本蚁群算法［6-8］，解决了对车辆进行多次派遣的问题。在算法实现中，设定先完成任务的车辆即返回原点，判断其是否满足其余还未运输路径的时间窗来判断此辆车是否接受第二次任务指派，这可以在保证时间窗的条件下使用较少的车辆数来完成任务，节省下来的车辆可以用来进行突发事件的配送或替代发生故障的车辆。

1 WTVRP数学模型构建

WTVRP问题是在VRP基础上提出的，一般定义为：已知n个工位点坐标及货物需求量，要求用m辆汽车在时间窗内从配送中心送达。每辆车的最大载荷确定，且每次配送量不能超过该车的最大载荷。每个工位点每次需求必须且只能由一辆车来满足［9］。笔者将所有车辆在任务时间内行驶距离最小作为该模型的优化目标，即：

式中：dij表示从工位i到工位j的行驶距离。

针对该数学模型，约束条件为式（2）～（7）：

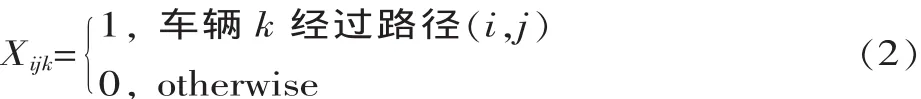
式中：Xijk为决策变量，表示第k辆车是否从工位i出发开向工位j，如果是，其值为1，否则为0。

式中：yik为决策变量，表示工位i的任务是否由车辆k完成，如果是，其值为1，否则为0。

式中：gi表示工位i的货物需求量；Qk表示牵引车k最大装载量。

式 （4）对车辆装载量进行约束，即每辆车在一条运输路径上货物装载量总和不能大于该车辆最大载荷。

式（5）确保每个工位的任务由一辆车来完成，且每个工位都得到了服务。

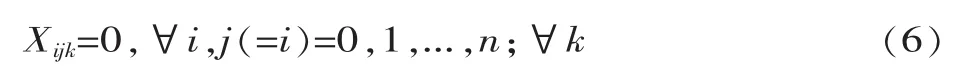
式（6）防止车辆在同一个工位点转圈。

式中：ti为车辆到达工位i的实际时间；si为对工位i的服务时间；Ei和Li表示到达工位i的最早时间和最晚时间范围。

式（7）确保车辆到达工位时不超出时间窗范围。

2 基本蚁群算法的改进

蚁群算法（AntSystem）是一种仿生优化算法，具备了并行自催化以及优良的分布式计算机制，鲁棒性较强［10］，该算法最初用来解决旅行商问题 TSP（Traveling SalemanProblem）。而WTVRP的复杂程度要远高于TSP，两者有一定相似性又存在许多差别。因此设计蚁群算法来求解VRTWP时，要充分结合WTVRP的具体要求，并借鉴蚁群算法求解TSP的经验。搜索时间长，易陷入局部最优，这是蚁群算法需要改进的缺点。

WTVRP与TSP的不同之处主要体现在表1所示的3个方面。

表1 WTVRP与TSP蚁群算法求解的差别

2.1 改进基本蚁群算法以实现WTVRP优化

Pij（ij）为模型中t时刻车辆k从工位i到工位j的转移概率，在满足装载量和时间窗前提下，主要由两方面因素决定：①通往下一城市路径长度以及路径上的信息量；②时间窗限制因素，即车辆等待时间较短优先原则和时间窗较小优先原则。因此，t时刻车辆k在工位i对下一个工位j的选择概率为：

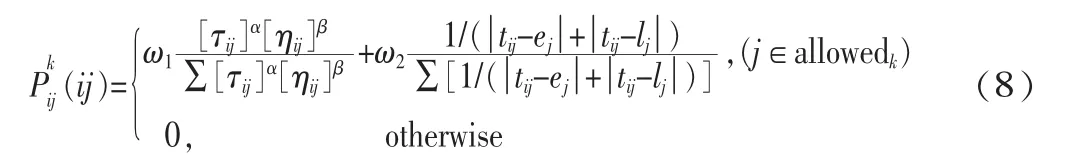
式中：τij和ηij分别表示信息素浓度和能见度；α为信息启式因子；β 为期望启发式因子；［ej，lj］表示工位 j点的时间窗；tij为由工位i到达工位j所需时间 （到达工位i服务的时刻+工位i服务时间+从工位i到j的行驶时间）；ω1和 ω2表示权重系数，均∈［0，1］，且有 ω1+ω2=1。

在这里ηij与解决TSP问题不同:

式中：ω（j）为在工位j的开始服务时间之前到达所需要的等待时间。

2.1.2 改进信息素更新方式

在基本蚁群算法中，每只蚂蚁遍历的路径都需要对其进行信息素的更新，这种方式收敛较慢，既拖延了计算时间，同时全局优化性能也不明显。本文保留了全局最优解，同时为了扩大信息素更新范围，避免陷入局部最优，选取每次迭代结果中前几位的“精英蚂蚁”进行信息素更新。

针对基本蚁群算法的缺陷，本文采用如下动态的信息素更新方式:

式中：△τgori为全局最优解或迭代最优解的倒数；ρ是信息素挥发系数。

在搜索过程中，先对局部信息素进行更新，当迭代到一定次数n时，整个系统进行一次全局信息素更新。接下来继续对局部最优信息素进行更新，两者交叉进行，直至达到算法中规定的最大迭代次数Nmax时停止。这样可以避免发生早熟现象，同时增加解的多样性，有效提升了算法性能和解的质量。

随着搜索次数的增加和信息素的更新，某个可行解上的信息量可能会出现极大值或极小值：极大值会导致搜索早熟，算法陷入局部最优使搜索停滞；极小值则会减缓收敛速度使求解过程延长。因此将每条轨迹上信息素限制在［τmin，τmax］之间，若 τij≤τmin，则 τij=τmin；若 τij≥τmax，则 τij=τmax。

算法初始时，信息素尚未更新，使用式（11)、(12）来确定 τmin和 τmax:

当信息素开始更新后则采用式（13）确定 τmax（t）：

式中：Lgb为通过PFIH算法构造初始可行解得到的可行路径总长度；σ为精英蚂蚁的个数，即每次循环中找出全局最优解的蚂蚁个数；τmin（t）不变。

2．2 蚁群算法参数组合选择

在蚁群算法中参数的选择直接影响到计算结果。根据具体问题不同，需要对参数进行相应调整，通过实验分析，下面方法可以快速选择出最优组合参数。

（1）城市规模/蚂蚁数目≈1．5，首先确定蚂蚁数。

（2）对取值范围较大的信息启发式因子α、期望启发式因子β、信息素强度Q进行粗调，来得到效果较好的解。

（3）对取值范围较小的信息素挥发因子ρ进行微调，提升最优解的效果。

重复以上步骤，直至得到理想参数组合。

2．3 车辆行驶状态的统计

在改进的蚁群算法中，单只蚂蚁k构成的可行解即可看作某一车辆的运输路径。算法中规定车辆完成运输任务即刻返回运输中心，返回运输中心的车辆在满足时间窗的条件下可以进行二次运输指派，即某一车辆完成的运输路径可以看作在时间窗约束下，多只蚂蚁构成可行解的集合，这里需要对满足约束条件的可行解进行有效合并。

为了获取车辆的行驶状态、所在工位、预计回到运输中心时间等信息，需要对全部车辆的状态进行跟踪，实现实时调度优化。因此需要建立车辆-时间状态图，用来查看车辆的状态。

具体实现过程为：对每辆车进行编号，并建立时间统计表。当第一辆车V1走完第一个子路径R0后回到原点，将回到原点时间t0记入时间统计表TV1中。接下来继续检测其它子路径的出发时间 t1，t2，t3……如果t1≥t0，那么车辆V1再次出发走路径R1，完成任务后返回原点，将时间t1记入时间统计表TV1中，将两条路径合并到车辆V1的行走路径表中，并把新路径的工位记入禁忌表。依次不断迭代，直到最后一次返回原点的时间无法满足剩余子路径出发时间要求时，然后才能派出新的一辆车。依照此模式直到走完所有子路径后，就可以得到最佳车辆数。

按照上面算法通过Matlab建立车辆—时间状态模型：纵坐标依次对派遣车辆进行编号，横坐标时间轴上采用不同颜色来显示车辆的不同行驶状态。根据图表，可以清楚了解到路上行驶的车辆和原点剩余车辆，以方便下一次车辆运送或处理突发事件。

3 算法实现

针对本文中车辆配送二次调度，对蚁群算法改进后，步骤如图1所示。

4 算例

▲图1 改进后蚁群算法流程图

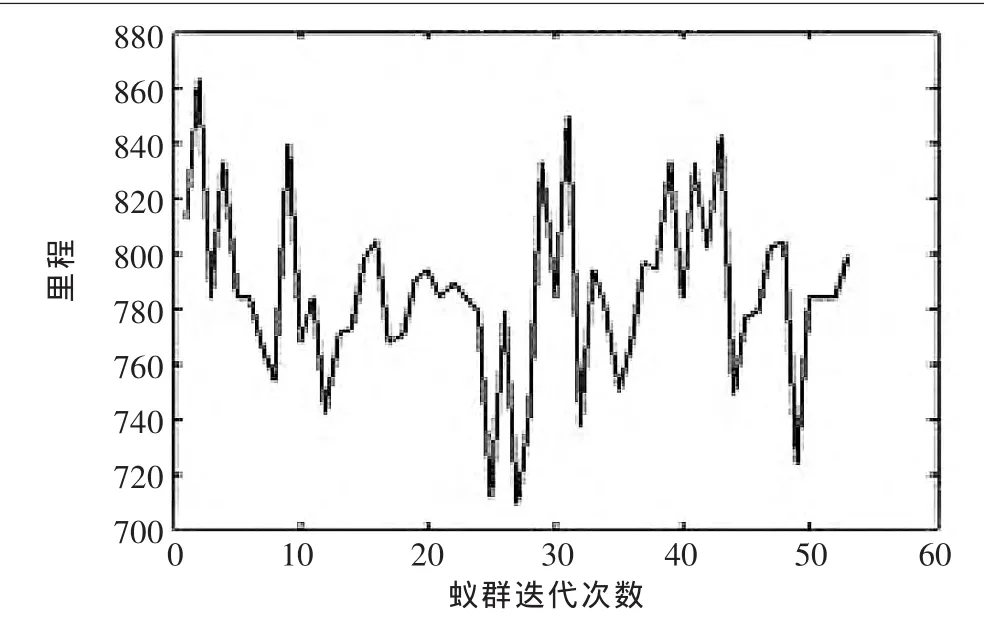
▲图2 改进前蚁群算法迭代次数与总路程的关系

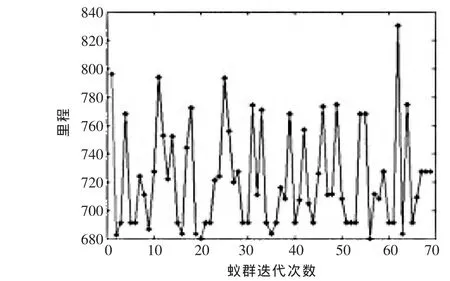
▲图3 改进后蚁群算法迭代次数与总路程的关系

选取数据模型见表2，模型中共22个坐标点，其中第一个坐标点为运输中心，车辆在230s内完成全部运输任务，货物量运输单位为kg。

表2 各工位需求信息

各参数取值为：蚂蚁数量m=15；根据以往经验和多次计算比较，取信息启发式因子α=0.9；期望启发式因子β=5；信息素挥发因子ρ=0.1；信息素强度Q=1；车辆载重为150kg，最大迭代次数为100次。

经过计算得到的最佳路径：Routes=

车辆V1: 1 14 7 22 1 0 0

车辆V2: 1 6 3 1 13 5 1

车辆V3: 1 21 2 1 0 0 0

车辆V4: 1 20 16 17 4 19 1

车辆V5: 1 18 10 11 12 1 0

车辆V6: 1 15 8 9 1 0 0

图2、图3分别为改进前、后蚁群算法迭代次数与总路程的关系，图中横坐标为迭代次数，纵坐标为里程数。由图2中可以看出，达到最佳里程数需迭代30次以上，而改进后（图3）的蚁群算法经过20次迭代即可达到最优值，从而保证了计算的时间限制。

改进后蚁群算法车辆巡回图如图4所示，车辆最佳里程数为680.465，改进前为706.538。蚁群算法改进后车辆—时间状态如图5所示，图中白色为车辆在原点停止时间段，黑色为车辆行驶时间段，深灰色为车辆在其它工位等待时间段，浅色为车辆服务时间段。从图中可以清晰显示出全部车辆任一时刻的状态。通过可行解路线进行合并对车辆进行二次指派，车辆2走完了工位6和3后返回原点，重新装载货物后对工位13和5进行了货物运送。

表3 改进前后结果对比

通过表3可以看出，改进后最佳里程数和得到最佳里程的迭代次数都好于改进前，缩短了行驶路程，同时提高了计算效率，并节省了一辆车辆。

5 结束语

本文针对VRPTW，建立了相应的基于时间轴的数学模型。通过改进的蚁群算法，首先排出最优路径，然后根据时间选择出可合并路径，从而得出最佳车辆数。运算时间和最佳里程数均有所优化。完成任务的车辆返回原点重新接受任务，提高了单辆车利用率，使带动态时间窗的车辆路径优化更加具有实际应用价值。

▲图4 改进后蚁群算法车辆巡回路线

▲图5 改进后蚁群算法车辆-时间状态图

［1］ 郎茂祥，胡思继．车辆路径问题的禁忌搜索算法研究［J］．管理工程学报，2004，18（1）:81-84．

［2］ 谢秉磊，郭耀煌，郭强．动态车辆路径问题：现状与展望［J］．系统工程理论方法应用，2002，11（2）:116-119．

［3］ 王训斌，陆慧娟，陈五涛．带时间窗动态车辆路径问题的改进蚁群算法［J］．工业控制计算机，2009，22（1）：41-43．

［4］ 郝会霞．基于改进蚁群算法的物流配送车辆路径优化方法的研究［D］．西安：长安大学，2008．

［5］ 郎茂祥．动态车辆配送优化调度问题的模型及其两阶段算法［J］．交通运输系统工程与信息，2009，9（4）：140-144．

［6］ 汪鹏飞．并行蚁群算法及其应用研究［D］．成都：西南交通大学，2008．

［7］ 刘霞．给予最大最小蚂蚁系统的动态车辆路径问题研究［J］．计算机工程与科学，2013，35（1）:130-137．

［8］ 王俊鸿，修桂华．二次蚁群算法在运输调度问题中的应用［J］．计算机应用与软件，2008，25（7）：71-73．

［9］ 陈迎欣．基于改进蚁群算法的车辆路径优化问题［J］．计算机应用研究，2012，29（6）:2031-2034．

［10］王君，李波，卢志刚．带时间窗动态车辆路径问题的优化调度策略［J］．计算机工程，2012，38（13）:137-141．