卧螺离心机内压力场的数值模拟
董连东,付双成,袁惠新
(常州大学机械工程学院,江苏 常州 213016)
研究开发
卧螺离心机内压力场的数值模拟
董连东,付双成,袁惠新
(常州大学机械工程学院,江苏 常州 213016)
卧螺离心机在高浓度固液混合物分离领域中应用广泛,其内部结构复杂,且封闭高速运转,对其内部流场实时监测难度大,缺乏对其内部流场特性的了解,进而影响对其分离性能的研究。本文应用计算流体力学软件Fluent,采用RNG k-ε湍流模型多重参考系(MRF)方法,模拟分析了卧螺离心机的内部流场,得到了压力场分布情况。结果表明:模拟液压值与理论液压值之间存在着一个差值,该差值是由于液体转动的滞后造成,且随着转鼓转速的增大而增大。同时还发现,静压、动压均随着径向位置的增大而增大,且静压梯度比动压大;沿转鼓轴向即往排液口方向,静压有递减的趋势,而动压逐渐增大。这可为进一步深入研究卧螺离心机提供参考。
卧螺离心机;压力场;数值模拟
卧式螺旋卸料离心机(简称卧螺离心机)是一种高速运转、连续进料、分离分级、螺旋推料器卸料的离心机[1-2]。自从第一台卧螺离心机诞生以来,由于它具有连续操作、处理量大、单位产量耗电量较少、适应性强等特点而得到了迅速发展[3-5]。
卧螺离心机通过离心力及螺旋与转鼓锥段对分离液产生挤压,促使固液分离,其内部压力场变化对分离液的运动规律以及分离效率有重要影响,因此,研究卧螺离心机内部压力场是十分必要的。卧螺离心机为高速旋转设备,其内部流场无法精确测量,随着计算机硬件条件和流体力学的飞速发展,采用数值模拟方法研究其内部的流场特征,是一种节省成本、方便省时的有效途径。黄志新、郑胜飞、于萍等[6-8]对卧螺离心机内部流场进行了初步研究,但由于模型的复杂性,其理论分析及模型建立均未考虑螺旋对于内部流场的影响,与实际工况相差较大。
本文考虑了螺旋的影响,利用Fluent软件,采用RNG k-ε湍流模型与多重参考系(MRF)进行求解,研究了卧螺离心机内部压力场,为优化离心机的结构设计提供重要参考。
1 控制方程和湍流模型
RNG k-ε模型[9]是对瞬时的Navier-Stokes方程用重整化群的数学方法推导出来的模型。模型中的常数与标准k-ε模型不同,同时增加了一些修正参数,这些参数使得RNG k-ε模型相比于标准k-ε模型对瞬变流和流线弯曲的影响能做更好的反应。可以计算低雷诺湍流,其考虑到旋转效应,对强旋流计算精度也有出色的表现。其湍动能与耗散率方程形式见式(1)、式(2)。

式中,Gk为由于平均速度梯度引起的湍动能产生;Gb为用于浮力影响引起的湍动能产生;YM为可压速湍流脉动膨胀对总的耗散率的影响。重整化群模型中,Cμ=0.09,C1ε=1.42,C2ε=1.68。αk和αε分别是湍动能 k和耗散率ε的有效湍流普朗特数的倒数。
2 模型简介及边界条件
卧螺离心机的模型结构及尺寸见图1和表1。对转鼓采用Cooper方法创建结构化网格,对螺旋采用T-grit方法创建非结构化网格。入口边界设定为速度入口,入口湍流强度为 5%,出口边界设为压力出口,压力为1.01×105Pa。
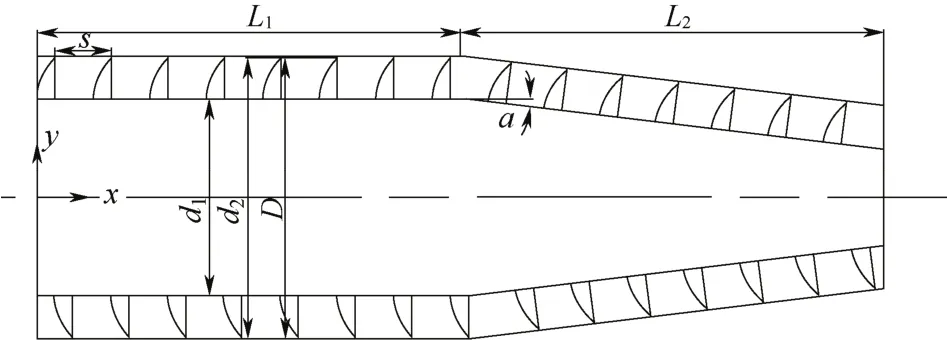
图1 卧螺离心机模型结构

表1 卧螺离心机几何模型基本尺寸
为分析方便,在z=0平面上,分别选择轴向位置为-100 mm、-150 mm、-200 mm、0 mm、100 mm、150 mm、200 mm、250 mm,径向位置为75 mm、80 mm、85 mm、90 mm的线,如图2所示。

图2 卧螺离心机模型在z=0截面上的截线(单位:mm)
3 模拟结果与分析
3.1 滞后系数的模拟
切向速度-半径关系如图3所示,切向速度沿半径方向逐渐增大(暂不考虑边界层),由公式v=rω,说明模拟正确。另外也可以看出模拟值小于理论值,这是因为当卧螺离心机工作时,转鼓旋转带动周围的液层一起转动,但液体的转动与转鼓转动并非一致,即存在所谓的滞后现象。
孙启才等[10]通过因次分析和对实验数据的回归处理,解N-S方程组,导出了旋流场下角速度场的计算公式,利用该公式计算的滞后值见表2中的文献计算值。表2中同时列出了数值模拟计算得到的滞后值,模拟滞后值与文献计算值相对误差在5%以内,进一步验证了模拟的正确性。
3.2 压力场模拟结果与分析
卧螺离心机工作时,处于转鼓中的液体和固体物料层,在离心力场的作用下,将给转鼓内壁以一定的压力,即离心液压。离心液压的计算公式见式(3)[1]。

图3 切向速度-半径关系(n=3500 r/min)

表2 不同转速下液体滞后比模拟值与文献计算值[10]比较

式中,pc为离心液压,Pa;ρ为物料密度,kg/m3;ω为转鼓角速度,r/s;R为转鼓半径,m;r为转鼓内物料环内表面半径,m。
转速与液压关系如图4所示,在linex=-200 mm至 linex=0处,随转鼓转速的增大,转鼓所受的液压增大,同时随着转速的增大,模拟液压与理论液压差距逐渐增大。例如在linex=-100 mm处,转速为300 r/min时,模拟液压为2.48 kPa,理论液压为2.51 kPa,液压差值为0.05 kPa,液压差值占理论液压的2%。转速为4000 r/min时,模拟液压为3.39 kPa,理论液压为4.46 kPa,液压差值为1.07 kPa,液压差值占理论液压的34%。由上文知,这是因为液体角速度与转鼓之间存在速度滞后现象,根据公式(3)可知,液压与转速ω成平方关系,所以,随着转速的增大,液体速度滞后的绝对值增大,模拟液压与理论液压差距增大,进一步证明了模拟的可靠性。目前,在卧螺离心机转鼓强度计算[11]中,关于离心液压的计算,往往取转鼓转速作为整个液层的转速,未考虑液体相对于转鼓的滞后,由图 3和图4可知,实际液体转速低于转鼓转速,即实际液压低于理论液压。这对于转鼓强度优化设计具有一定指导作用。
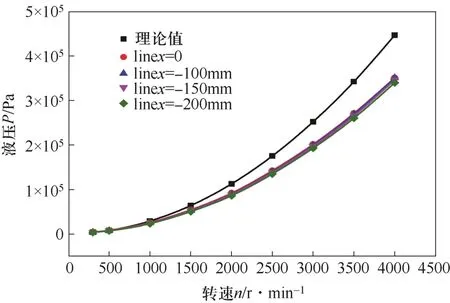
图4 液压-转速关系
3.2.1 静压模拟
为研究方便,下文以转速为3500 r/min为例,分析卧螺离心机内部压力场。不同截面静压分布云图如图5所示,柱段、锥段半径与静压关系分别如图6、图7所示,静压与轴向位置的关系如图8所示。由图5知,静压沿半径方向逐渐增大,有明显的压力梯度在转鼓内壁处达到最大,且对称性较好,静压力基本符合强制涡[12]流场压力变化规律。但是,在锥段部分静压没有柱段部分那样分布规则,这是由于通过螺旋推料器与转鼓锥段共同对转鼓段处的固体沉降层产生双向挤压力,迫使污泥固相颗粒的相互挤压,使污泥脱水,清液回流。
由图6可知,柱段内不同截面上的静压-半径关系曲线基本趋于重合,说明静压的轴向梯度值比较小。由图7可知,在锥段部分,静压沿径向逐渐增大但增长速度比柱段小,linex=300 mm为小端出料处,与大气相连,所以静压接近为0。
由图8可知,从进口向溢流口方向,静压力有递减的趋势。同时在接近溢流板位置随着液环半径的增大,静压力迅速增加,这在一定程度上有利于液体的排出,但是过大的压力差可能会导致转鼓内壁剩余的固体颗粒泛起,不利于沉渣,从而使溢流液体含渣率上升。所以,应该尽可能降低压力差。从进口向小端出料口方向,静压力减小,且趋势比较明显。图8中,曲线不是连续的,断开的部分为螺旋。
3.2.2 动压模拟
动压是由于卧螺离心机高速旋转所产生的附加力,表征液体动能的大小。不同截面动压如图9所示,柱段、锥段内半径与动压关系分别如图10、图11所示,轴向位置与动压关系如图12所示。

图5 不同截面静压分布云图

图6 柱段内静压-半径关系

图7 锥段内静压-半径关系

图8 静压-轴向位置关系
由图9知,动压沿半径方向逐渐增大,并且增大的速度逐渐加强,在转鼓内壁处达到最大值。由图10知,柱段内不同截面上的动压-半径关系曲线与动压不同,并不重合,这是由于沿径向,液体速度不同,所以动压不同。由图10、图11知,在靠近螺旋转筒壁面处,动压逐渐降低,这是因为动压表征动能的大小,根据动能公式E=0.5 mv2,可知动能与速度密切相关。螺旋转筒高速旋转,由于液体有黏度,由普朗特边界层理论[13]知,螺旋转筒壁附近存在速度梯度区,所以在边界层动压逐渐降低。同样也可看出,在转鼓内壁处,动压从壁面向内部迅速降低。
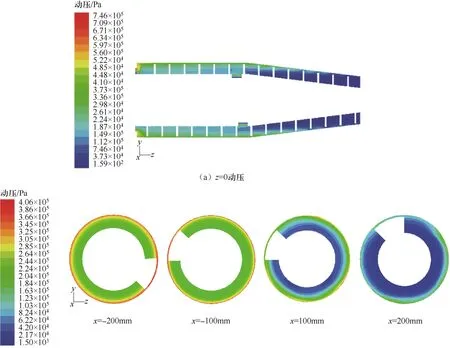
图9 不同截面动压
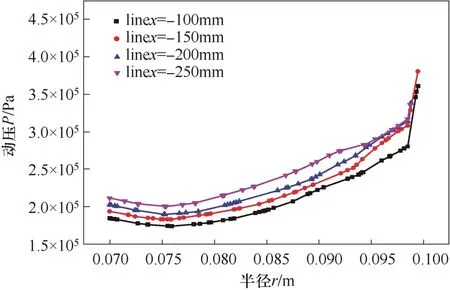
图10 柱段动压-半径关系
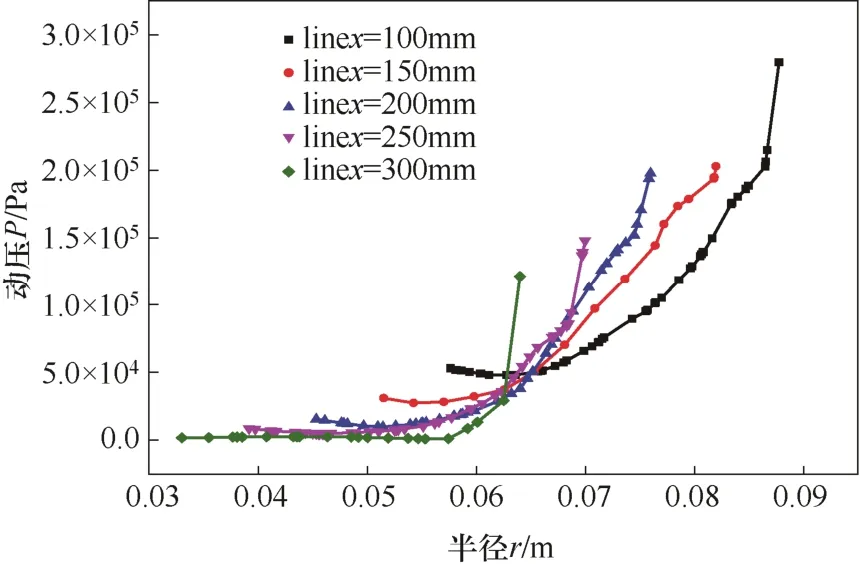
图11 锥段动压-半径关系

图12 动压-轴向位置关系
由图12知,动压在溢流口处变化较大,动压沿轴向位置,总体趋势从大端向小端逐渐降低。由此也可以看出,靠近螺旋壁面,存在边界层,动能从螺旋壁面向流道降低,符合普朗特边界层理论。在靠近大端偏上部分,动压迅速增大,这是因为,液体流到大端处,受大端阻挡及螺旋作用。而在liney=75 mm靠近大端处,动压迅速降低,是因为受溢流口影响。
4 结 论
采用Fluent中RNG k-ε湍流模型多重参考系(MRF)方法Euler模型,考虑了螺旋的影响,模拟了卧螺离心机内的三维全流场,进一步明确了流场内各物理量的分布,得到如下结论。
(1)随转鼓转速的增大,转鼓所受的液压增大,同时随着转速的增大,模拟液压与理论液压差距逐渐增大。转速为300 r/min时,模拟液压是理论液压的98.7%;转速为4000 r/min时,模拟液压是理论液压的78.51%。
(2)转鼓内静压梯度较大,沿半径方向逐渐增大,在转鼓内壁处达到最大,且对称性较好,基本符合强制涡流场压力变化规律。沿轴向即往排液口方向,静压力有递减的趋势。同时在接近溢流板位置,随着液环半径的增大,静压力迅速增加,这在一定程度上有利于液体的出流,但是迅速变化的压力差,可能会导致转鼓内壁剩余的固体颗粒泛起,使溢流液体含渣率上升。
(3)动压沿半径方向逐渐增大,并且增大的速度逐渐加强,在转鼓内壁处达到最大值。靠近壁面处,受液体黏度影响,存在边界层,速度梯度较大,动能从壁面向流道内降低,符合普朗特边界层理论。沿轴向向溢流口方向,动压逐渐增大,与静压变化趋势相反。
[l] 孙启才,金鼎五. 离心机原理结构与设计计算[M]. 北京:机械工业出版社,1987.
[2] 袁惠新. 分离过程与设备[M]. 北京:化学工业出版社,2008.
[3] Giuseppe Altieri. Comparative trials and an empirical model to assess throughput indices in olive oil extraction by decanter centrifuge[J]. Journal of Food Engineering,2010,97(1):46-56.
[4] 俞雷霖,奚立峰,俞如友. 离心分离技术的国内现状国外进展及大规模定制设计[J]. 化学世界,2006,47(11):696-699.
[5] Beveridge T,Harrison J E. Juice extraction with the decanter centrifuge:sweet and sour cherries,peaches and apricots[J]. Food Research International,1995,28(2):173-177.
[6] 黄志新,钱才富,范德顺,等. 沉降离心机圆形转鼓内液面速率的数值模拟[J]. 北京化工大学学报,2007,34(6):645-648.
[7] 郑胜飞,任欣,谢林君. 卧螺离心机流场的三维数值模拟[J]. 轻工机械,2009,27(6):26-29.
[8] 于萍,林苇,王晓彬,等. 卧螺离心机离心分离场速度仿真分析[J]. 机械工程学报,2011,47(24):151-157.
[9] Yakhot V,Orszag S A. Renormalization group analysis of turbulence:Basic theory[J]. Journal of Scientific Computing,1986,1(I):1-51.
[10] 孙启才,曾凡骏. 沉降离心机转鼓内流体角速度场的研究[[J]. 流体工程,1990(11):1-5.
[11] 全国分离机械标准化技术委员会. JB/T 8051—2008. 离心机转鼓强度计算规范[S]. 2008-02-01.
[12] 柳吉祥. 旋转流分选的理论及应用[M]. 北京:煤炭工业出版社,1985.
[13] 陈玉璞,王惠民. 流体动力学[M]. 北京:清华大学出版社,2013.
Numerical simulation on pressure field in a decanter centrifuge
DONG Liandong,FU Shuangcheng,YUAN Huixin
(School of Mechanical Engineering,Changzhou University,Changzhou 213016,Jiangsu,China)
Decanter centrifuges have been widely used for the separation of solid-liquid mixtures with high solid concentration. The real-time monitoring of the flow field inside the centrifuge is believed to be difficult because of its complexity in structure and closed operation at high speed of rotation. RNG k-ε turbulent model and MRF method based on the FLUENT software of computational fluid dynamic technology were used in this research to simulate the pressure field in the centrifuge. Results showed that the differences between simulated and theoretical hydraulic pressure caused by the lag of liquid rotation increased with increase in rotational speed. The static pressure and dynamical pressure increased with radius,and the gradient of static pressure was greater than that of dynamical pressure. The static pressure increased along the drum axis from the inlet to liquid discharge port,while the dynamical pressure decreased gradually. It could be used as guidance for researching the performance of decanter centrifuges.
decanter centrifuge;pressure field;numerical simulation
TK-9
A
1000-6613(2014)02-0309-06
10.3969/j.issn.1000-6613.2014.02.007
2013-07-24;修改稿日期:2013-08-19。
科技部科技型中小企业创新基金(08C26213200648)及江苏省2013年度高校研究生科研创新计划项目(CXLX13_724)。
董连东(1987—),男,硕士研究生。E-mail dld2011@ 163.com。联系人:袁惠新,教授。E-mail yuanhuixin2000@126.com。

