无梯度多参数自动历史拟合方法

张 凯,路然然,周文胜,姚 军,潘彩霞,沙雁红

(1.中国石油大学石油工程学院,山东青岛 266580;2.中海油研究总院,北京 100027)

无梯度多参数自动历史拟合方法

张 凯1,路然然1,周文胜2,姚 军1,潘彩霞2,沙雁红2

(1.中国石油大学石油工程学院,山东青岛 266580;2.中海油研究总院,北京 100027)

通过历史拟合以降低油藏地质参数的不确定性,提出一种稳定高效的无梯度多参数最优化调参技术,根据贝叶斯统计理论建立历史拟合最小化数学模型,并利用奇异值分解算法进行降维分解,然后采用基于方向导数的无梯度算法对该最优化问题进行求解。该方法同时实现了渗透率、孔隙度、相对渗透率、原油黏度及水体参数的拟合,进一步降低了反问题的不确定性。与人工历史拟合结果相比,基于降维方法的自动历史拟合结果表现出高度的一致性,节省了大量的人力与机时,证明了该方法的有效性与正确性。

油藏;自动历史拟合;贝叶斯理论;奇异值降维分解;无梯度算法

以贝叶斯理论[1-2]为基础的自动历史拟合[3]数学模型目前已得到国内外学者的普遍认可。目前存在3种主导的历史拟合求解方法。梯度类方法稳定性差,代码编写繁重:Chen应用了有限差分法(FDM)[4-5],Anterion提出了梯度模拟器法[6]; Zhan[7]、Li[8]、Sarma[9]、Rodrigues[10]分别对伴随方法[7-10]进行了研究。集合卡尔曼滤波方法(EnKF)由Naevdal等[11]引入石油工程领域,但对于强非线性或非高斯问题,EnKF难以对未知性进行描述。随机性方法可以找到全局最优解,更为简单易行,Ouenes[12]、Sen[13]、Deutsch[14]运用了模拟退火算法;Reis[15]和Cullick[16]运用了人工神经网络算法。为了改善随机性算法计算效率低的不足,笔者提出一种基于奇异值[17]降维分解的无梯度求解算法。

1 油藏多参数最优化调参问题描述

1.1 目标函数

从统计意义上讲,反问题的解通常符合一定的概率分布。基于贝叶斯理论确定油藏模拟历史拟合问题的目标函数,既能保证拟合模型与先验模型估计吻合,又使实际生产观测数据与模拟计算值之间的误差最小,得出的模型参数更符合油藏实际地质统计规律。目标函数的表达式为

式中,x为由油藏参数组成的Nx维向量,如孔隙度、渗透率及饱和度等参数;xav为先验油藏模型估计; CX为基于先验地质信息,依据地质统计学方法生成的Ne个符合均值为xav的初始油藏模型实现的协方差矩阵,其对角元素恰好为各油藏参数的方差,CX∈RNx×Nm;dobs为Nd维向量,包含实际观测数据如含水率、产油量、压力等;g代表油藏系统,这里主要是指油藏数值模拟器;CD为观测数据测量误差协方差矩阵。

1.2 优化的变量参数

控制变量x是由油藏参数组成的Nx维向量。本研究可以同时实现孔隙度、渗透率及饱和度、相对渗透率、原油黏度、油水界面等参数的拟合,即

式中,k为每个网格的渗透率所组成的向量;φ为每个网格的孔隙度所组成的向量;s为每个网格的饱和度所组成的向量;假设油藏共有N个网格,则k、φ、s都为N维向量;μp为二维原油黏度拟合参数向量;aq为9维水体水侵影响程度拟合向量(假设水体为一维解析模型);kr为相对渗透率拟合参数向量,当只拟合油水相渗和毛管力时,kr为7维向量; x为3N+18维向量;当同时拟合油水相渗和油气相渗时,kr为14维向量,x为3N+25维向量。

1.2.1 相对渗透率参数化过程

假设油水相对渗透率曲线及油水毛管力曲线均符合幂率函数形态,采用式(3)～(5)进行参数化。拟合时只需调整公式中的参数xr=(nw,no,nwoc,aw, ao,awoc,Pmin)T。这样不仅减少了拟合参数,降低了拟合成本,而且保证相渗曲线规律不发生变化,减少了拟合的随机性,提高了拟合精度。油气两相的参数化方式与油水两相的参数化方式相同,

式中,Swc、Sor和Sw分别为束缚水、残余油和含水饱和度;Krw和Kro分别为水相相对渗透率和油相相对渗透率;Pwoc为油水毛管力;aw、ao和awoc为可调系数;nw、no和nwoc为可调幂率指数;Pmin为最小油水相毛管力。

1.2.2 黏度曲线参数化过程

地层原油黏度对压力十分敏感。当压力低于饱和压力时,随压力降低,气体从原油组分中分出,原油黏度呈幂率模式急剧增加;当压力高于饱和压力时,随压力下降,原油体积膨胀,黏度呈直线降低;当压力等于饱和压力时,原油体积达到最大值,此时原油黏度最低。因此,最优化调参时原油黏度随压力的变化可以按式(6)和(7)来进行参数化,通过修改μp=(nμ,aμ)T来拟合黏度－压力曲线,

式中,μ为原油黏度,mPa·s;μob为饱和压力下的原油黏度,mPa·s;p为地层压力,MPa;pb为原油的泡点压力,MPa。

1.2.3 边底水拟合

油气藏水体会对油气藏(尤其是气藏)的开发动态造成显著影响,须加以考虑。本文中采用半解析方法[18]估计水体,以利用Van Ecerdingen-Hurst非稳态解析模型计算水侵量得到的解作为精确解。假设水体参数为

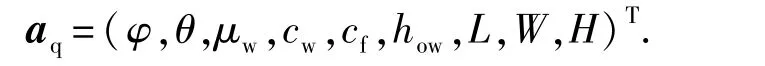
式中,φ为水体孔隙度;θ为水体夹角;μw为水的黏度,mPa·s;cw和cf分别为水和水体岩石的压缩系数,MPa－1;how为油水界面值,m;L、W、H分别为水体的长度、宽度和厚度,m。

利用aq可计算水体响应参数如水体流出量S及水体时间T。S描述一定的压力降对应的累积水体流出量,T描述水体对油藏压力变化的反应速度,S和T的表达式分别为

2 基于方向导数的历史拟合问题求解

2.1 目标函数奇异值分解

对于实际油藏历史拟合问题,所需反演的油藏参数的维数Nx通常数以万计,这对于目标函数O(x)的优化极其困难,而且操作矩阵所需的计算代价在实际应用中也难以承受。为此,提出一种基于初始多模型实现的奇异值降维分解法,该方法可近似地对历史拟合问题目标函数进行降维处理,有效地避免矩阵的计算,为大规模油藏历史拟合问题提供新思路。

式中,矩阵Xδ第j列向量为(x－xav);xj为第j个初始模型实现。

对矩阵Xδ进行奇异值分解可得,

U和V中分别是Xδ的奇异向量,而Λ是Xδ的奇异值。CX的正交单位特征向量组成U,特征值组成ΛTΛ,CTX的正交单位特征向量组成V,特征值(与CX相同)组成ΛΛT。由于VTV=INe,则

通常参数个数Nx远大于初始模型个数Ne。因此,Ns≤Ne。仅考虑模型中的奇异值向量,则

CX的伪逆矩阵可表示为

利用CX的伪逆矩阵^C－1X代替目标函数中的则N维关于x的优化问题降为N维关于x的

xs优化问题,避免维数高达几十甚至上百万的协方差矩阵CX的求逆过程,大大简化了计算难度,提高了计算效率,最终方程变为

2.2 基于方向导数的无梯度算法优化求解

2.3 参数边界的约束

沉积环境在成因上制约了储层的岩性、物性、孔隙结构、束缚流体、可动流体等不同的变化特征[19]。以河流相[20]为例,主流河道的渗透率一般要高于近河道亚环境的渗透率。因此利用地质统计学等理论建立模型及参数优化调整时,都须对参数进行相控约束(图1),以免最终模型脱离沉积相地质模型而失去拟合意义。添加相约束后,对数变换将处于[xlowi,xupi]值域内的模型变量xi转化为(－∞,+∞)值域内的变量si,从而将关于xi的约束优化问题转变成关于变量si的无约束优化问题,

图1 沉积相约束模型Fig.1 Sedimentary facies constraint model

2.4 多参数自动历史拟合流程

多参数拟合基本流程如图2所示。

图2 求解流程Fig.2 Solution flowchart

3 基于降维的无梯度历史拟合方法的优势

分别对伴随梯度及集合卡尔曼滤波(EnKF)方法的优势及劣势进行简单的介绍,并与上述所提出的方法进行对比。

3.1 伴随梯度算法

(1)优势:伴随梯度算法能够直接获取真实梯度,结合最优化搜索,仅计算两次油藏数值模拟,以最快的速度就能完成进行单一时间的历史拟合。

(2)劣势:①历史拟合是长期的,甚至长达几十年,也就是以月为单位存在几百个月,尽管单一时间梯度算法速度最快,但是对于几百个单一时间,速度就得不到保障,例如,拟合总时间为20 a,一共240个月,完成一次迭代就需要240×2=480次数值模拟,历史拟合又是一个最小化问题,需要多次迭代,一次数值模拟时间可能长达数小时,工作量巨大;②伴随梯度算法求解需要用到油藏数值模拟流动方程构建的雅可比矩阵,需要与模拟器耦合才能完成求解,这里的雅可比矩阵维数高达数百万,构建过程复杂,对于小尺度问题能够完成较好的拟合,但是对于大规模复杂油藏及组分模拟求解较为困难。

3.2 集合卡尔曼滤波算法

(1)优势:①EnKF算法多个模型同时参与计算,考虑地质统计学因素,可较好地刻画地层非均质性,预测油藏模型;②动态的观测数据可以随时间步实时持续吸收,稳定性好,不需要从头运行模拟器及拟合旧数据,计算周期短;③EnKF更新模型的过程中只须模拟器的计算结果,而无须关注解的过程,可以在任意油藏模拟器的基础上自动更新计算,不用进行复杂的敏感计算。

(2)劣势:①由于观测数据随时间步实时持续吸收,每次都须重启动模型,需要读取数百万维的数据,运行效率低;②EnKF拟合过程是线性的,对于具有很强非线性的油藏数值模拟问题拟合效果较差;③对于地质条件复杂的油藏,多模型计算可能导致油藏数值模拟器计算不收敛,无法预测最终效果。

3.3 基于奇异值分解的降维自动历史拟合方法

(1)优势:①基于奇异值分解的降维自动历史拟合方法,不需要分时间步来进行数值模拟,完成一次迭代仅需几次数值模拟,并且不需要每步存储读取数据,因此对于同样多的数值模拟次数和同样长的拟合时间,相对于EnKF方法速度更快;②多个模型同时参与计算,但实际更新过程中仅更新平均模型,不存在油藏数值模拟器计算不收敛的问题;③较之EnKF方法,降维方法能够较好地解决历史拟合非线性求解问题;④迭代过程中仅对初始平均模型进行更新,也就是最终只推荐一个拟合油水参数的油藏模型,方便现场应用。

(2)劣势:降维方法虽然降低了模型的不确定性,推荐的单一模型便于现场应用,但是由于只对一个模型进行更新,因此该方法刻画地层非均质性的能力下降。

综上所述,对于大规模复杂油藏,降维求解方法是现阶段技术条件下真正能够用于油田实际的自动历史拟合技术。

4 算例分析

4.1 理论实例

基于油藏数值模拟软件及奇异值降维方法对一个25×25的二维非均质油藏模型进行多参数调参,模型的真实渗透率场如图3所示。首先基于序贯高斯模拟生成了100个初始油藏模型实现,由于添加了相约束,各实现均能很好地把握油藏的真实特征,尤其是比较准确地反映出了高渗条带的位置。用这些模型实现的平均值作为初始先验模型估计,调整渗透率拟合油藏生产数据,以证明方向导数优化方法的正确性。

图3 二维非均质油藏真实渗透率场Fig.3 Real permeability field in 2D heterogeneous reservoir

图4为渗透率场、油田日产油及井底流压的拟合结果。随控制变量迭代更新,渗透率场逐步接近真实渗透率场,刻画出了高渗条带的位置及方向,从而拟合指标曲线从初始模型数据不断靠近真实油藏观测数据;最优拟合曲线与历史数据几乎完全重合,证明了基于贝叶斯理论的降维分解算法的有效性。

图4 渗透率场、日产油量和井底流压拟合结果Fig.4 Matching results of permeability field,oil rate and bottomhole pressure

图5为单次数值模拟实践与模型更新次数之间的关系曲线。由图5可知,随着模型更新次数的增加,拟合模型越来越接近真实模型,数值模拟所耗费的时间也越来越短。

图5 单次数值模拟时间与模型更新次数之间的关系Fig.5 Relationship between time of single simulation and number of model updates

4.2 油田实例

4.2.1 油藏地质与开发概况

QD油田位于渤海中部海域,是一个大型复杂河流相稠油油田,地层原油黏度为28～260 mPa· s。该油田是在前第三纪古潜山(石臼坨凸起)背景上发育起来的被断层复杂化的大型低幅度披覆构造,储层为正韵律和复合韵律河道沉积砂体。油藏埋深浅(0.9～1.6 km),储层胶结疏松,物性好(平均孔隙度35%,平均渗透率3 μm2);纵向上含油层段多,油柱高度小(小于20 m),油水关系复杂。油质稠,投产初期生产状况差,基本没有无水采油期。4.2.2 拟合结果对比

采用2002年1月1日到2009年10月23日的动态数据对QD油田进行拟合。由于水体数据、孔隙度及原油黏度比较准确,因此只拟合含水率、累积产油量、油藏渗透率、饱和度及相对渗透率数据。

含水率、累积产油量及相对渗透率自动历史拟合效果与人工历史拟合效果对比如图6所示。由图6可见,人工拟合效果与自动历史拟合效果几乎完全一致,证明了无梯度自动历史拟合方法的有效性。

图7为人工自动历史拟合及最终反演得到部分层位的渗透率的MAP估计。对比两种拟合方法所得到的油藏模型渗透率发现,两种法拟合结果具有高度的一致性,均能很好地把握油藏的真实特征,能够准确地反映出高渗条带的位置。

图8为饱和度场拟合结果。两种拟合方法得到的结果具有高度的一致性。

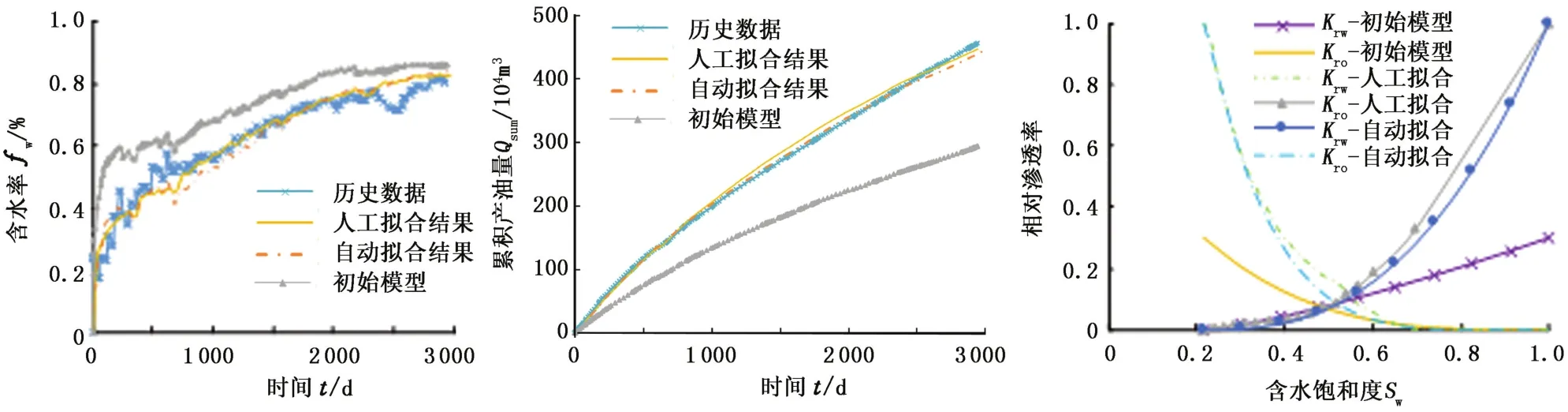
图6 不同方法的含水率、累积产油量及相对渗透率拟合结果Fig.6 Matching results of water cut,accumulative oil production and relative permeability by different matching methods

图7 第61层渗透率场拟合结果Fig.7 Matching results of permeability field of 61st stratum

图8 第68层饱和度场拟合结果Fig.8 Matching results of oil saturation field of 68th stratum

5 结 论

(1)基于降维的无梯度自动历史拟合方法,可以较好地刻画地层非均质性,并解决多模型计算油藏数值模拟器不收敛的问题,是现阶段技术条件下能够用于油田实际的一种高效自动历史拟合技术。

(3)自动历史拟合方法省时省力,对工作人员的经验要求低,拟合效果与人工历史拟合结果具有相似的精度,是一种高效易操作的多参数调参技术。

[1] OLIVER D S,REYNOLDS A C,LIU N.Inverse theory for petroleum reservoir characterization and history matching[M].New York:Cambridge University Press,2008.

[2] OLIVER D S.On conditional simulation to inaccurate data[J].Math Geology,1996,28(6):811-817.

[3] 闫霞,张凯,姚军,等.油藏自动历史拟合方法研究现状与展望[J].油气地质与采收率,2010,17(4):69-73.

YAN Xia,ZHANG Kai,YAO Jun,et al.Review on automatic history matching methods for reservoir simulation [J].Petroleum Geology and Recovery Efficiency,2010, 17(4):69-73.

[4] CHEN W H,GAVALAS G R,SEINFELD J H,et al.A new algorithm for automatic history matching[J].SPE Journal,1974,14(6):593-608.

[5] SARMA P,AZIZ K,DURLOFSKY L J.Implementation of adjoint solution for optimal control of smart wells[R].SPE 92864,2005.

[6] ANTERION F,EYMARD R,KARCHER B.Use of parameter gradients for reservoir history matching[R].SPE 18433,1989.

[7] WU Zhan,REYNOLDS A C,OLIVER D S.Conditioning geostatistical models to two-phase production data[J].SPE Journal,1999,4(2):142-155.

[8] LI R,REYNOLDS A C,OLIVER D S.History matching of three-phase flow production data[R].SPE 87336, 2003.

[9] SARMA P,AZIZ K,DURLOFSKY L J.Implementation of adjoint solution for optimal control of smart wells[R].SPE 92864,2005.

[10] RODRIGUES J,WAECHTER A,CONN A,et al.Combining adjoint calculations and Quasi-Newton methods for automatic history matching[R].SPE 99996,2006.

[11] NEVDAL G,MANNSETH T,VEFRING E H.Nearwell reservoir monitoring through ensemble kalman filter [R].SPE 75235,2002.

[12] OUENES A,BHAGAVAN S.Application of simulated annealing and other global optimization methods to reservoir description:myths and realities[R].SPE 28415, 1994.

[13] SEN M K,DATTA-Gupta A,STOFFA P L,et al.Stochastic reservoir modeling using simulated annealing and genetic algorithm[J].SPE Formation Evaluation, 1995,10(1):49-56.

[14] DEUTSCH C,JOURNEL A.The application of simulated annealing to stochastic reservoir modeling[J].SPE Advanced Technology Series,1994,2(2):222-227.

[15] LEANDRO Reis.Risk analysis with history matching using experimental design or artificial neural networks [R].SPE 100255,2006.

[16] CULLICK A,JOHNSON W,SHI G.Improved and more rapid history matching with a nonlinear proxy and global optimization[R].SPE 101933,2006.

[17] TAVAKOLI R,REYNOLDS A C.History matching with parameterization based on the SVD of a dimensionless sensitivity matrix[J].SPE Journal,2010,15(2):495-508.

[18] GLEGOLA M,DITMAR P,HANEA R,et al.History matching time-lapse surface-gravity and well-pressure data with ensemble smoother for estimating gas field aquifer support-a 3D numerical study[R].SPE 161483,2012.

[19] 裘亦楠.石油开发地质方法论(三)[J].石油勘探与开发,1996,23(4):42-45.

QIU Yinan.The methodology of petroleum development geology:Ⅲ[J].Petroleum Exploration and Development,1996,23(4):42-45.

[20] 俞启泰.河流相、三角洲相渗透率平面分布数值抽象地质模型[J].新疆石油地质,1999,20(4):314-319.

YU Qitai.The numerical abstract geological models of permeability plane distribution for flucial and delta facies[J].Xinjiang Petroleum Geology,1999,20(4):314-319.

(编辑 李志芬)

Multi-parameter gradient-free automatic history matching method

ZHANG Kai1,LU Ranran1,ZHOU Wensheng2,YAO Jun1,PAN Caixia2,SHA Yanhong2
(1.School of Petroleum Engineering in China University of Petroleum,Qingdao 266580,China; 2.CNOOC Research Institute,Beijing 100027,China)

The uncertainties of the reservoir geological parameters can be reduced by history matching.A stable and efficient multi-parameter optimal adjustment technology was proposed in this work.This technology involved setting up a mathematical minimization model of history matching based on Bayesian statistical theory and reducing the dimension of parameters by singular value decomposition method.And the optimization problem was finally solved by using gradient-free method based on directional derivative.By using this method,permeability,porosity,relative permeability curve,viscosity of crude oil and the oil-water interface parameters can be matched at the same time to further reduce the uncertainties of the inverse problem.Compared with manual history matching,automatic history matching results based on dimension reduction method show a high degree of consistency which proves the effectiveness and the correctness of this method.Automatic history matching process is also proved to be capable of saving a lot of human and machine labor.

reservoir;automatic history matching;Bayesian theory;singular value decomposition;gradient-free method

TE 34

A

1673-5005(2014)05-0109-07

10.3969/j.issn.1673-5005.2014.05.015

2013－10－23

国家自然科学基金项目(61004095);国家重大专项(2011ZX05024－002－008);高等学校博士学科点专项科研项目(20100133120003)

张凯(1980－),男,副教授,博士,从事油气田开发工作。E－mail:reservoirs@163.com。

张凯,路然然,周文胜,等.无梯度多参数自动历史拟合方法[J].中国石油大学学报:自然科学版,2014,38 (5):109-115.

ZHANG Kai,LU Ranran,ZHOU Wensheng,et al.Multi-parameter gradient-free automatic history matching method[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38(5):109-115.