非饱和多孔介质层中Love波频散特性

邵长金,崔为涛,赵 哲,戴乐根

(中国石油大学理学院,北京 102249)

非饱和多孔介质层中Love波频散特性

邵长金,崔为涛,赵 哲,戴乐根

(中国石油大学理学院,北京 102249)

为建立更准确的地层反演模型,基于非饱和多孔介质本构关系,用连通率处理上面两层间的边界条件,理论推导出三层非饱和多孔介质中Love波的频散方程,计算分析多阶模态Love波频散曲线。结果表明,Love波第1阶模态没有截止频率,对2阶以上模态,阶数越高截止频率越大。各阶模态的Love波最大速度趋近半空间层的横波速度,而最小速度趋近第1层横波速度。Love波速曲线以第2层横波速度为界分为上下两簇,各模态均在第2层横波波速处衔接。模态不同,衔接处曲线的光滑程度不同,模态越高,光滑程度越好。对各参数的敏感性分析表明,孔隙度、饱和度、连通率、黏滞系数和渗透率的变化对Love波相速度影响敏感性依次减小。

Love波;非饱和多孔介质;频散特性;连通率;敏感性分析

针对不同介质中Love波的频散现象,许多学者开展了研究工作。Ewing等[1]用理想弹性介质模型解释Love波传播频散机制,后来马兴瑞等[2-4]讨论了弹性半空间上覆弹性介质层中的Love波。Deresiewicz[5-6]首先将上覆介质变更为多孔介质,并将Biot[7-8]波动模型引入到液体饱和多孔介质中Love波的理论研究,建立了弹性介质半空间上覆液体饱和多孔介质层中Love波的频散方程,但没有进一步求解给出频散和衰减曲线。夏唐代[9]、汪越胜[10-11]等分别用有限元方法和迭代法计算给出了多模态频散曲线,认为频散取决于频率和厚度的乘积,速度最大值和最小值分别在截止频率和无穷大频率处。柯燎亮[12]、周凤玺[13]等考虑了介质参数的非均匀性,用迭代法和回传射线矩阵法推导出非均匀饱和土层中Love波的频散方程;而对非饱和的多孔介质层,陈炜昀等[14]研究了弹性半空间上覆非饱和多孔介质层中Love波的频散、位移、衰减等性质,得出Love波存在多模态频散,且与饱和度有关,第1阶模态没有截止频率,高阶模态饱和度越高截止频率越低。此外,Shishir等[15-16]分析了边界条件、初始应力等对Love波频散特性的影响。从研究对象看,对多层非饱和多孔介质层中Love波的研究较少,同时,非饱和多孔介质中各参数对Love波的传播有何影响,目前的研究工作还不够深入。在路基维护等实际工程中,人们希望通过Rayleigh波或Love波获得路面下方多至3～4层的详细分层信息,此时的实际情况更接近于非饱和半空间上覆多层非饱和多孔介质层,为准确反演上覆非饱和多孔介质层数和层厚,充分了解多层多孔介质中Love波频散规律以及各参数对频散的影响是必要的。笔者推导非饱和半空间上覆两层非饱和多孔介质层中Love波频散方程,引入连通率的概念处理非饱和多孔介质层之间界面问题,用数值方法求得Love波频散曲线。

1 非饱和多孔介质层中Love波的频散方程

1.1 模型的建立

非饱和多孔介质层由介质半空间和两个上覆层组成,上覆层分别标记为第1层和第2层,第1层厚度为h1,第2层厚度为h2,用第3层标记无限半空间,这三层都是非饱和多孔介质。建立的笛卡尔坐标系如图1所示。假定波传播方向沿着x正方向,Love波振动方向沿着y方向,其中x－y平面在第1层与空气水平分界面上,z轴垂直向下指向半无限空间。

1.2 控制方程

非饱和多孔介质的本构关系[17-18]为

式中,Nss、Nsl、Nsl、Nll、Nlg、Ngg为独立参量;μs为固体骨架的剪切模量;ns、nl、ng分别为多孔介质中固体骨架、液体、气体的体积分数;ρs、ρl、ρg分别为相应三相的密度;ξl、ξg分别为液体和固体、气体和固体的耦合作用系数。其中,耦合作用系数可由如下公式[19-20]计算:

式中,ηl和ηg分别为液体、气体黏度;κ为该多孔介质的绝对渗透率;分别为液体和气体的相对渗透率。相对渗透率与饱和度Sr的关系可用目前应用较广的VG模型描述[21]:

式中,m为VG模型[21]参数。

Love波只有y上的位移分量,可令固体、液体、气体的位移为简谐形式:

由于是切变波,体应变应为零,利用这一条件,将位移表达式(8)代入本构关系,可得

slg固、液、气三相之间的耦合作用。液体、气体的位移与固体骨架位移之间有如下关系式:从式(13)～(15)可以看出和这些参数只影响固体、液体、气体的密度和体积分数即平均密度,对固体剪切模量μs没有影响。

1.3 边界条件

由于非饱和多孔介质层之间流体可能产生交换,使得边界条件较为复杂,实际地层中层与层之间并不是完全独立的,多孔介质中的流体之间存在互相渗透和流动,需要引入参数来表征上层流体的交换。不失一般性,假定第1层和第2层边界上孔隙间可以交换流体,第3层为半无限空间,与上层之间流体交换渗透对其影响可以忽略,每层介质中孔隙是均匀完全开孔的,可在每层中任意流动,并且流动不改变固体骨架的形态和位置。

为描述层间的流体交换,引入一个新的参数连通率Δ(0≤Δ≤1),它表征了单位法向矢量为i⇀的表征面元上的孔隙之间的连通性,与孔隙介质的结构以及孔隙中流体的性质有关。如图2所示。

图2 连通示意图Fig.2 Sketch map of connectivity

假设界面两侧介质的孔隙开口面积分别为S1和S2,两侧开口孔隙的重叠面积为SΔ,则SΔ=其中0≤Δ≤1。例如,Δ=0表征上层的孔隙开口面积和下层孔隙开口面积没有重叠面积,开口完全错开,这时两层之间不存在连通;Δ=1表征上层的孔隙开口面积和下层孔隙开口面积有最大重叠面积。

假定第1层和第2层的流体可以自由流动,则作用后的各层中体积分数为

考虑流体交换后,各层中的波数表达式变为

考虑Love波在第1层上表面、第1层与第2层分界面、第2层与第3层交界面上的连续性,即位移连续和应力连续,有

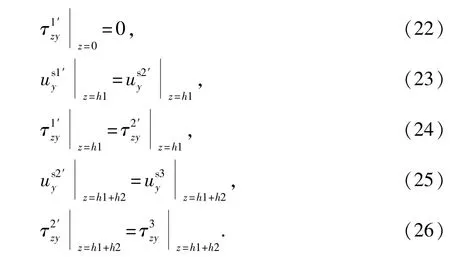
Biot介质中的应力关系[7-8]:

要使方程组有非零解,系数行列式必为零,即

上式即为非饱和多孔介质层中Love波的频散方程。

2 数值计算和分析

为说明Love波的频散与各个物理参数之间的关系,参考路面和地基情况,计算选取的各层物理参数见表1。用MATLAB编程对三层非饱和多孔介质中Love波的频散特性进行数值计算。

表1 非饱和多孔介质基本参数Table 1 Basic parameters of unsaturated porous media

2.1 Love波多阶模态频散特性

图3给出了Love波多阶模态(n=1,2,,9)相速度(VL)曲线以及横波波速(Vsh)曲线。图中,三条横线从上到下依次为第3、2和1层的横波速度(Vsh3,Vsh2和Vsh1),以第2层横波速度为界分为上下簇,上一簇曲线为第3和第2层介质间的Love波,从左到右依次为1～9阶模态。下一簇曲线为第2和第1介质层间的Love波,从左到右依次为1～3阶模态。从图4可以看出第1阶模态下Love波没有截止频率(fc),从第2阶模态开始的高阶模态都存在fc,且fc随着阶数的增高而增大。

图3 多阶模态Love波频散曲线Fig.3 Multi-modal dispersion curves of Love waves

从上一簇曲线可以看出,第3和第2层介质间的Love波各阶模态波速VL在频率较低时趋近第3层横波速度Vsh3,频率较高时趋近第2层横波波速Vsh2,且变化趋势变缓。这是由于Love波是由第3和第2层介质中的横波叠加产生的。频率较低时,波长较大,Love波能量主要集中在第3层介质中,第3层的横波波速高且起主导作用,使得Love波速度较大。同理,频率较高时横波波速较低的第2层起主导作用,Love波能量主要集中在第2层介质中,使得Love波速度较小。

从下一簇曲线可以看出,第2和第1层介质间的Love波各阶模态波速的变化趋势与上一簇变化相近,Love波各阶模态波速VL在频率较低时趋近Vsh2,频率较高时趋近Vsh1,且变化趋势变缓。

从图3整体可以看出,第2和第1层介质间的Love波最高波速VLmax与第3和第2层介质间的Love波最低波速VLmin相等,这是由于三层介质之间是紧密耦合的。上下两簇曲线各模态均在第2层横波波速频率处衔接,满足这一条件的频率记为fVL=Vsh2。模态不同,衔接处曲线的光滑程度不同,第1阶模态最不光滑,随着模态的递增,光滑程度越来越好。这种情况的产生,可能是中间层的影响。

2.2 Love波频散曲线敏感性

Love波相速度与多孔介质中孔隙度、饱和度、连通率、液体黏滞系数、渗透率等参数直接相关。为了进一步研究多孔介质中各参数变化对频散曲线的影响,需要首先分析不同频率时Love波频散曲线对各参数的敏感程度。Feng等[22]将相速度敏感性定义为参变量扰动后与扰动前相速度的变化量与扰动前相速度之比,可以表示为式中,Si为相速度的敏感性,代表第i个频率点第j个地层参数的敏感性;V为相速度;fi为给定的频率点;xj为地层模型中孔隙度等变化参数。

对表1中孔隙度、饱和度、连通率、液体黏滞系数、渗透率等参数取10%增量来计算Love波第1模态到第3模态频散曲线对各参数敏感程度,结果见图4。

图4 不同参数下Love波敏感性曲线Fig.4 Sensitivity analysis of Love waves to different parameters

由图4可以看出:①孔隙度的变化对Love波相速度影响最大,饱和度、连通率、黏滞系数的敏感性依次减小,渗透率的敏感性非常小(以下讨论忽略渗透率)。②所有参数敏感性随频率、模态的不同有所变化,在某个频率达到峰值(图4(a))或谷值(图4(b)～(d)),在频率满足f=fVsh2=VL时,敏感度产生突变,峰值/谷值和突变点随模态增高均向高频移动。孔隙度的变化对Love波的相速度影响为正相关,存在峰值,峰值随模态增大依次变大;饱和度、黏滞系数的影响为负相关,存在谷值,谷值随模态增大均依次变小;连通率的影响在f＜fVsh2=VL前为负相关,在f＞fVsh2=VL后为正相关,存在谷值,谷值随模态增大依次变小;渗透率的影响时正时负,且影响非常小。③各模态Love波相速度对每一参数敏感性曲线没有重合现象,但变化趋势相似,峰值/谷值和突变点出现在不同的频率段,且在较高频率后几乎完全分离,可以分频率段提取,这意味着Love波反演时容易识别各模态。④比较图3和图4可以看出,各种参数对Love波相速度影响敏感性不同,敏感性曲线的变化趋势均不同,意味着各参数间具有较好的独立性,因此若用多种参数进行Love波反演,可提高反演的准确性。

从图3可以看出,Love波频散曲线第1阶模态没有截止频率,高阶模态(n≥2)有截止频率且变化形态相似,有较好的规律性,便于观察和分析。从图4可以看出孔隙度、饱和度、连通率对频散曲线影响较大。

图5 不同孔隙度第2阶模态Love波频散曲线Fig.5 The second order modal dispersion curves of Love waves under different porosity

2.3 孔隙度对Love波频散特性影响

只改变表1中孔隙度进行计算,图5给出了不同孔隙度(φ=0.1,0.3,0.5,0.7)时第2阶模态Love波相速度频散曲线。图中,从下到上孔隙度依次为0.1至0.7。Love波第2阶模态的VLmax、VLmin、fc和fVL=Vsh2均随着孔隙度的增大依次增大。由式(13)可以得出,随着介质孔隙度的增大,每层的平均密度均减小,即横波波数减小,横波速度均增大,三层介质中横波叠加产生的Love波VLmax、VLmin、VfVL=Vsh2均增大。此外,结合图4(a)、图5中Love波第2阶模态孔隙度敏感性曲线,可看出孔隙度对Love波频散影响较大,为正相关,相邻曲线之间区分明显,对Love波相速度频散曲线影响明显。

2.4 饱和度对Love波频散特性影响

改变表1的饱和度,其他参数保持不变,计算不同饱和度(Sw=0.1,0.3,0.5,0.7)时第2阶模态Love波相速度频散曲线,如图6。图中,从左到右饱和度依次为0.7至0.1。Love波第2阶模态的VLmax、VLmin、fc和fVL=Vsh2均随着饱和度的增大依次减小,这是由于随着介质饱和度的增大,由公式(13)可以得出,每层的平均密度均增大,即横波波数增大,层中横波速度均减小,三层介质中横波叠加产生的Love波VLmax、VLmin、VfVL=Vsh2也随之减小。此外,结合图4(b)、图6中第2阶模态敏感性曲线可看出饱和度对Love波频散影响比孔隙度影响小,为负相关,相邻曲线之间区分较明显,对Love波相速度频散曲线影响较明显。

图6 不同饱和度第2阶模态Love波频散曲线Fig.6 The second order modal dispersion curves of Love waves under different saturations

2.5连通率对Love波频散特性影响

只改变表1中连通率进行计算。不同连通率(Δ=0.2,0.6,1.0)时第2阶模态Love波相速度频散曲线见图7。可以看出,不同Δ时第2阶模态VLmax相等。由式(16)～(18)可见,由于Δ只改变上两层介质中的横波速度,未改变半空间的横波速度,因此VLmax趋近于Vsh3。Love波的第2阶模态VLmin随Δ增大而增大,这是由于当Δ增大时,Vsh1增大,Vsh2降低,VLmin趋近于Vsh1。在上下两簇衔接处即f= fVL=Vsh2处,频散曲线随Δ变化的趋势发生了转折,上一簇曲线中Δ越大VL越小,下一簇曲线中的VL越大。此外,结合图4(c)、图7中第2阶模态敏感性曲线可看出,虽然Δ对Love波频散影响较小,但在f＜fVL=Vsh2时为负相关,在f＞fVL=Vsh2时为正相关,敏感性在f=fVL=Vsh2处存在正负突变,因此连通率对Love波相速度频散的影响不能忽视。

图7 不同连通率第2阶模态Love波频散曲线Fig.7 The second order modal dispersion curves of Love waves under different connection rate

3 结 论

(1)三层非饱和多孔介质中Love波多模态频散特性明显,第1阶模态没有截止频率,高阶模态(n≥2)有截止频率,随着模态增高,截止频率变大, Love波各阶模态最大速度趋近半空间中的横波速度,最小速度趋近第1层中的横波速度。

(2)三层非饱和多孔介质中Love波的传播分为两部分,波速以第2层横波速度为界,频率较低时,Love波在第3和第2层介质间传播,频率较高时,Love波在第2和第1层介质间传播。Love波速以第2层横波速度为界分为上下两簇曲线,各模态均在第2层横波波速处衔接,模态不同,衔接处曲线的光滑程度不同,第1阶模态最不光滑,随着模态的递增,光滑程度越来越好。

(3)孔隙度、饱和度、连通率、黏滞系数和渗透率的变化对Love波相速度影响敏感性依次减小,孔隙度的影响为正相关,饱和度、黏滞系数的影响为负相关,连通率影响的相关性会在某频率下正负突变。

(4)孔隙度、饱和度和连通率等参数对Love波相速度影响具有较强独立性,若采用多参数、多模态同时用于Love波反演,可以提高反演的准确性。

[1] EWING W M,JARDETZKY W S.Elastic waves in layered media[M].McGraw-Hill:New York-Toronto-Lon-don,1957.

[2] 马兴瑞,章梓茂,邹振祝,等.广义Love波的频谱研究[J].应用力学学报,1992,9(1):103-108.

MA Xingrui,ZHANG Zimao,ZOU Zhenzhu,et al.Researching on spectra of generalized Love waves[J].Chinese Journal of Applied Mechanics,1992,9(1):103-108.

[3] 杨奎.面波多模频散曲线的敏感性及特征分析[J].物探化探计算技术,2012,34(4):436-443.

YANG Kui.Analysis of sensitivity and characteristics of multi-mode dispersion curves of surface wave[J].Computing Techniques for Geophysical and Geochemical Exploration,2012,34(4):436-443.

[4] 马志杰,董连成.Love波相速度频散曲线敏感性比较[J].山西建筑,2008,4(12):121-122.

MA Zhijie,DONG Liancheng.The comparison of the sensibility of Love wave speed frequency dispersion curve [J].Shanxi Architecture,2008,4(12):121-122.

[5] DERESIEWICZ H.The effect of boundaries on wave propagation in a liquid filled porous solid:II.Love waves in a porous layer[J].Bull Seism Soc Am,1961,51:51-59.

[6] DERESIEWICZ H.The effect of boundaries on wave propagation in a liquid-filled porous solid:Ⅵ.Love waves in a double surface layer[J].Bulletin of the Seismological Society of America,1964,54:417-423.

[7] BIOT M A.Theory of propagation of elastic waves in a fluid saturated porous solid:I.low frequency range[J].Acoust Soc Am,1956,28(2):168-178.

[8] BIOT M A.Theory of elastic waves fluid-saturated porous solid:II.high frequency range[J].The Journal of the Acoustical Society of American,1956,28(1):179-191.

[9] 夏唐代,王立忠,吴世明.饱和土中Love波弥散特性[J].振动工程学报,1994,7(4):357-362.XIA Tangdai,WANG Lizhong,WU Shiming.Dispersion characteristics of Love wave in saturated soil[J].Journal of Vibration Engineering,1994,7(4):357-362.

[10] 汪越胜,章梓茂,于桂兰.饱和土层中Love波的传播特性[J].振动工程学报,1998,11(2):177-183.

WANG Yuesheng,ZHANG Zimao,YU Guilan.Properties of Love waves in a saturated soil layer[J].Journal of Vibration Engineering,1998,11(2):177-183.

[11] WANG Y S,ZHANG Z M.Propagation of love waves in a transversely isotropic fluid-saturated porous layered half-space[J].The Journal of the Acoustical Society of American,1998,103(2):695-701.

[12] 柯燎亮,汪越胜,章梓茂.非均匀饱和土中Love波的传播特性[J].岩土力学,2004,25:369-374.

KE Liaoliang,WANG Yuesheng,ZHANG Zimao.Properties of Love waves in inhomogeneous saturated soil [J].Rock and Soil Mechanics,2004,25:369-374.

[13] 周凤玺,赖远明,宋瑞霞.非均匀饱和土中平面波的传播特性[J].中国科学:科学技术,2013,43(2):131-140.

ZHOU Fengxi,LAI Yuanming,SONG Ruixia.Propagation of plane wave in non-homogeneously saturated soils [J].Scientia Sinica Techologica,2013,43(2):131-140.

[14] 陈炜昀,夏唐代,王志凯,等.非饱和地基中Love波的传播特性[J].振动与冲击,2012,31(17):22-25.

CHEN Weiyun,XIA Tangdai,WANG Zhikai,et al.Propagation characteristics of love waves in unsaturated soil[J].Journal of Vibration and Shock,2012,31(17): 22-25.

[15] SHISHIR G,SUMIT K V,DINESH K M,et al.Possibility of Love wave propagation in a porous layer under the effect of linearly varying directional rigidities[J].Applied Mathematical Modelling,2013,37(6):652-660.

[16] SUMIT K V,SHISHIR G,DINESH K M.Influence of rigid boundary on the love wave propagation in elastic layer with void pores[J].Acta Mechanica Solida Sinica,2013,26(5):551-558.

[17] WEI C,MURALEETHARAN K K.A continuum theory of porous media saturated by multiple immiscible fluids: I.linear poroelasticity[J].International Journal of Engineering Science,2002,40(16):1807-1833.

[18] WEI C,MURALEETHARAN K K.A continuum theory of porous media saturated by multiple immiscible fluids: II.Lagrangian description and variational structure[J].International Journal of Engineering Science,2002,40 (16):1835-1854.

[19] GARG S K,NAYFEH A H.Compressional wave propagation in liquid and or gas saturated porous media[J].Journal of Applied Physics,1986,60(9):3045-3055.

[20] BERRYMAN J G,THIGPEN L,CHIN R C.Bulk elastic wave propagation in partially saturated porous solids [J].Journal of the Acoustical Society of America,1988, 84(1):360-373.

[21] VAN G M.A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J].Soil Science Society of America Journal,1980,44(5):892-898.

[22] FENG S,SUGIYAMA T,YAMANAKA H.Application of sensitivity analysis to array design for microtremor array survey:proceedings of the 104th SEGJ Conference [C].Tokyo:The Saciety of Exploration Geophysicists of Japan(SEGJ),c2001.

(编辑 修荣荣)

Dispersion characteristics of Love wave in unsaturated layered porous media

SHAO Changjin,CUI Weitao,ZHAO Zhe,DAI Legen
(College of Science in China University of Petroleum,Beijing 102249,China)

Using connectivity factor to handle the boundary condition between the two upper layers,the Love wave dispersion equation for three layers in an unsaturated porous media was derived based on the constitutive relations,and then the multimode Love wave dispersion curves were calculated numerically.The results indicate that,for the second or higher order Love wave modes,the higher the mode order,the larger the cut off frequency,in contrary to the fundamental mode Love wave which doesn't have cutoff frequency.The maximum velocity of Love waves for all the modes asymptotically reaches the shear wave velocity of the half-space,while the minimum velocity reaches the shear wave velocity in the top layer.The Love wave velocity curves for all the modes are separated by,but are also linked to the shear wave velocity in the second layer.The smoothness of the velocity curves is controlled by the mode number:the higher the mode,the better the smoothness.Analyses show that the sensitivity of Love wave phase velocity to different parameters decreases with the order of the following parameters:porosity,saturation,connectivity factor,viscous coefficient and permeability.

Love wave;unsaturated porous media;dispersion characteristics;connectivity factor;sensitivity analysis

O 429

A

1673-5005(2014)05-0059-07

10.3969/j.issn.1673-5005.2014.05.008

2014－02－20

中国石油大学(北京)基本科研基金(KYJJ2012－06－26)

邵长金(1964－),男,教授,博士,研究方向为应用声学。E－mail:sh00668@163.com。

邵长金,崔为涛,赵哲,等.非饱和多孔介质层中Love波频散特性[J].中国石油大学学报:自然科学版, 2014,38(5):59-65.

SHAO Changjin,CUI Weitao,ZHAO Zhe,et al.Dispersion characteristics of Love wave in unsaturated layered porous media[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38(5):59-65.