基于连通导电理论和HB方程的骨架导电纯岩石电阻率模型
宋延杰,李晓娇,唐晓敏,付 健
(1.东北石油大学地球科学学院,黑龙江大庆 163318; 2.非常规油气成藏与开发省部共建国家重点实验室培育基地,黑龙江大庆 163318)
基于连通导电理论和HB方程的骨架导电纯岩石电阻率模型
宋延杰1,2,李晓娇1,唐晓敏1,2,付 健1
(1.东北石油大学地球科学学院,黑龙江大庆 163318; 2.非常规油气成藏与开发省部共建国家重点实验室培育基地,黑龙江大庆 163318)
针对现有导电模型很难描述骨架含导电矿物黄铁矿的岩石导电规律的难题,利用骨架完全由导电颗粒组成的人造岩样以及骨架部分由导电颗粒组成的天然和人造岩样的岩电实验数据,研究水电阻率和导电颗粒体积分数变化对岩石导电规律的影响,得出骨架导电纯岩石的地层因素与孔隙度及电阻增大系数与含水饱和度在双对数坐标上为非线性关系,随水电导率减小或导电颗粒体积分数增大,地层因素和电阻增大系数值降低。根据骨架导电纯岩石的组成,结合连通导电理论特点,将骨架导电纯岩石分为不导电骨架相、导电骨架相和自由流体相。基于连通导电方程只能描述单一导电相的两相混合介质导电规律而HB方程能描述两相均导电的混合介质导电规律的特点,基于连通导电理和HB方程建立骨架导电纯岩石电阻率模型。结果表明,骨架导电纯岩石电阻率模型预测的地层因素与孔隙度以及电阻增大系数与含水饱和度的理论关系与实验规律相符且模型满足物理约束,该模型能够描述骨架完全和部分由导电矿物组成的纯岩石的导电规律,可用于定量评价骨架导电低阻油层的饱和度。
纯岩石;黄铁矿;连通导电理论;HB方程;电阻率模型
近几年的勘探开发实践表明,低阻油气藏是复杂油气藏中最具潜力的主要研究对象之一,而且在某些油田的低阻油气藏发现了含导电矿物黄铁矿的低电阻率油层[1-5]。虽然含导电矿物黄铁矿的低阻油层数量较少,但是随着油气资源的需求与日俱增,这类骨架导电低阻油层将具有一定的开采价值。骨架含导电矿物的油气层与常规油气层相比,导电机制发生变化,导电规律变得更复杂,而现有电阻率解释模型多是在Archie公式基础上建立的,很少能描述骨架含一定量导电矿物的纯岩石导电规律。目前,有关骨架导电的电阻率模型主要有以下几种:①岩石骨架导电模型[6-8],虽然在模型中引入了岩石骨架导电概念,但未给出骨架导电项与导电颗粒体积分数和电阻率的具体表达形式,因此该模型不能用于描述导电颗粒体积分数变化的骨架导电纯岩石的导电规律。②混合泥质砂岩有效介质电阻率模型[9-12],虽然这些模型考虑了导电矿物引起的岩石骨架导电,但是没有将骨架颗粒分成导电的骨架颗粒和不导电的骨架颗粒两种,因此不适用于描述骨架含一定量导电矿物的纯岩石导电规律,只能用于描述骨架完全由导电矿物组成的纯岩石的导电规律。③含黄铁矿泥质砂岩含水饱和度模型[13],虽然该模型可用于描述骨架含一定量导电矿物的泥质岩石导电规律,但是当泥质体积分数为零时,该模型转变为黄铁矿颗粒和纯砂岩的并联导电,这对于描述黄铁矿颗粒在岩石骨架中呈分散状的纯岩石导电规律是不适用的,因此该模型不适用于描述由分散状导电矿物引起的骨架导电纯岩石导电规律。④修正的Archie公式[14-15],基于饱含水骨架导电人造岩样的电阻率测量及考虑边界条件的传统Archie公式,提出了适用于饱含水骨架导电岩石的修正Archie公式;在此基础上给出适用于n相介质的通用修正Archie公式,该式可用于描述骨架由部分导电颗粒组成的骨架导电纯岩石的导电规律。笔者基于骨架导电岩石的岩电实验数据,研究导电骨架颗粒体积分数和电阻率变化对岩石导电特性的影响,将连通导电理论和HB方程结合建立骨架导电纯岩石电阻率模型。
1 骨架导电岩石导电规律实验
利用骨架完全或部分由导电颗粒组成的人造或天然岩心的岩电实验数据[4-5,14],研究骨架导电特性对地层因素(F)与孔隙度(φ)关系以及电阻增大系数(I)与含水饱和度(Sw)关系的影响。
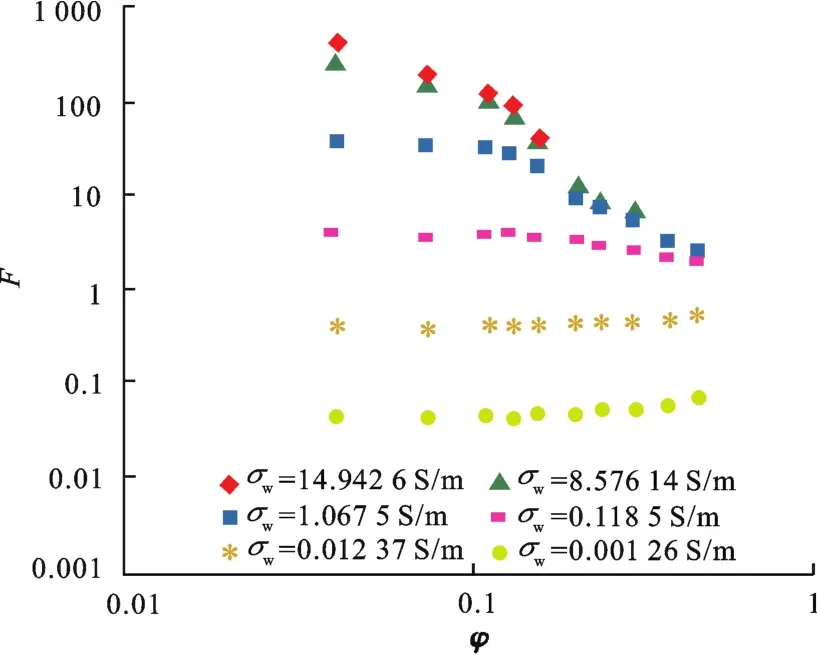
图1 骨架完全由导电颗粒组成人造岩样的F与φ关系Fig.1 Relationships between F and φ for artificial samples with matrix composed entirely of conductive grains
Glover等制作了10块骨架完全由导电颗粒组成的人造岩样[14],导电骨架颗粒由氧化铜组成,其电阻率近似为32.47 Ω·m,岩样的孔隙度为4%~44%,水的电导率为0.001 26~14.942 6 S/m,测量了饱和不同水电导率的岩样电导率。图1给出了10块骨架完全由导电颗粒组成的人造岩样在6种水矿化度下的地层因素与孔隙度实验关系。可以看出,在双对数坐标上地层因素与孔隙度之间的关系为非线性关系;当骨架电阻率大于水电阻率时,地层因素值大于1.0,而当骨架电阻率小于水电阻率时,地层因素值小于1.0;当孔隙度相同时,地层因素值随水电导率增大而增大;对应不同水电导率的地层因素值之差随孔隙度增大而逐渐减小。
Clavier等[4]利用10块黄铁矿体积分数不同的全直径砾岩样品,测量了5种频率(19 Hz,35 Hz, 280 Hz,1 kHz,20 kHz)下饱和地层水电导率为16.7,10,2,1.0 S/m的岩样复电阻率,岩样的孔隙度为4.15%~22.5%,黄铁矿体积分数为0.0%~27.3%。图2(a)给出了10块骨架含有不同体积分数黄铁矿的全直径砾岩岩样的地层因素值与孔隙度实验关系。Clennell等利用澳大利亚北部大陆边缘气田黄铁矿体积分数不同的25块岩心样品(井1岩心样品10块(去掉了3块黏土体积分数较大的岩样),井2岩心样品8块,井3岩心样品7块)和5块人造岩心样品进行了黄铁矿对岩石电阻率影响程度的研究[5],岩样的孔隙度为3.8%~32.2%,水的电导率1.71~2.75 S/m,黄铁矿体积分数为0.0%~12%。图2(b)给出了25块骨架含有不同体积分数黄铁矿的砂岩岩样和5块人造岩样的地层因素值与孔隙度实验关系。从图2中可以看到,对于骨架部分由导电颗粒组成的岩石,在双对数坐标上地层因素值与孔隙度为非线性关系;在低孔隙度处,随着导电颗粒体积分数的增高,地层因素值明显降低;对应不同导电颗粒体积分数的地层因素值之差随孔隙度增大而逐渐减小,这是因为随孔隙度增大,导电骨架颗粒的体积分数减小,因此导电骨架颗粒体积分数变化对地层因素值的影响变小。
Clavier等利用等粒径的石英颗粒制作了纯石英砂岩样品[4],在纵向不同位置处测量了该样品在饱含水和近似束缚水饱和度情况下的电阻率,该样品的孔隙度为40.4%,地层水电阻率为0.0599 Ω·m,黄铁矿颗粒体积分数为0%。同时,利用等粒径的石英颗粒和黄铁矿颗粒制作了3种相同黄铁矿颗粒体积分数的纯石英砂岩样品,在纵向不同位置处分别测量了3种样品在饱含3种矿化度水和近似束缚水饱和度情况下的电阻率,3种样品的孔隙度为40.5%、42%、41%,地层水电阻率为0.0596、0.306、0.51 Ω·m,黄铁矿颗粒体积分数为16.5%。图3给出了上述4种样品的电阻增大系数与含水饱和度的关系。从图中可以看到,随导电颗粒体积分数增大,电阻增大系数降低;随着水电阻率增大,电阻增大系数降低。
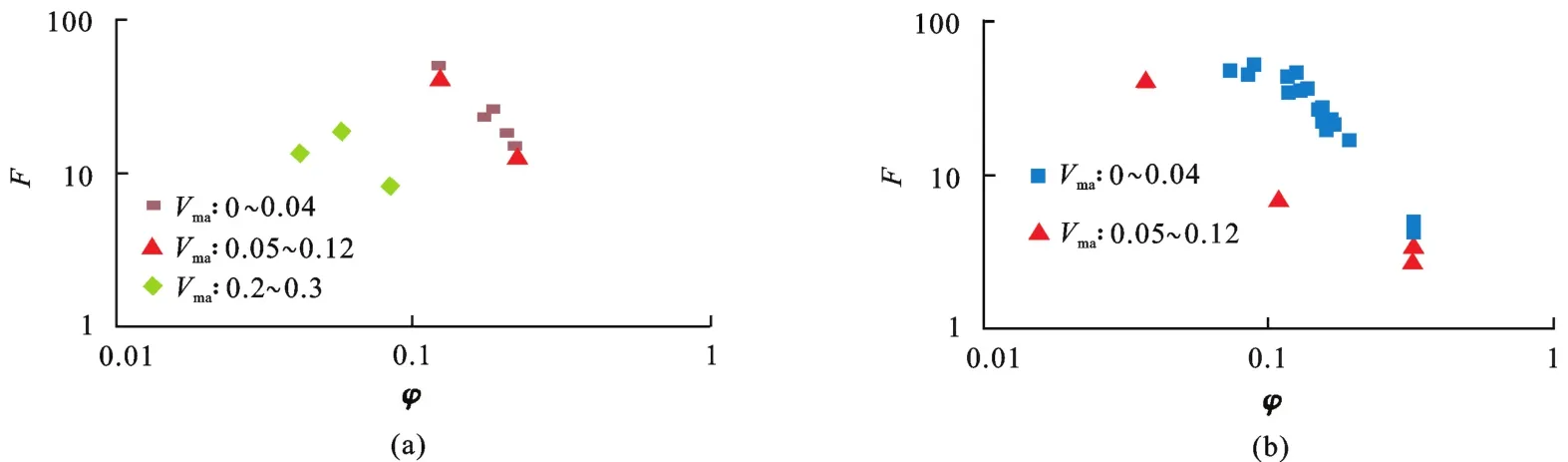
图2 骨架部分由导电颗粒组成的岩样的F与φ关系Fig.2 Relationships between F and φ for samples with matrix composed partially of conductive grains

图3 骨架部分由导电颗粒组成岩样的I与Sw关系Fig.3 Relationships between I and Swfor samples with matrix composed partially of conductive grains
2 导电纯岩石电阻率模型
2.1 连通导电方程和HB方程
连通导电方程引入了两个新参数:导电指数和水连通校正系数,这两个参数均与孔隙的几何形状和水在介质中的分布状态有关,而且水连通校正系数可以解释水在孔隙中的连通作用,因此连通导电方程可以更好地描述岩石的孔隙结构和水的连通性对岩石导电性的影响[16-19]。对于骨架不导电的含油气纯岩石,其连通导电方程为

式中,σt为岩石电导率,S/m;σw为地层水电导率, S/m;φw为含水孔隙度;Xw为水连通性校正系数;μ为导电指数。
当Xw很小时,1-Xw近似为1.0,则式(1)可简化为

HB方程可以用于描述导电或不导电连续相介质中聚集着导电或不导电分散相的两相混合物的导电规律,在低频情况下HB方程的形式[20-21]为

式中,σ为混合物的电导率,S/m;σP为分散相的电导率,S/m;σc为连续相的电导率,S/m;Vp为分散相的体积分数;Lp为分散相的去极化因子;mp为分散相的胶结指数。
2.2 骨架导电纯岩石电阻率模型
对于骨架部分由导电矿物组成的纯岩石,其组分为不导电的骨架颗粒、导电的骨架颗粒、不导电的油气和水。根据连通导电理论,将骨架导电纯岩石地层划分为不导电骨架相、导电骨架相和自由流体相。其中,不导电骨架相由不导电骨架颗粒和相应的束缚水组成,导电骨架相由导电的骨架颗粒和相应的束缚水组成,自由流体相由可动水和油气组成。图4给出了基于连通导电理论和HB方程的骨架导电纯岩石电阻率模型的体积模型,其物质平衡方程为
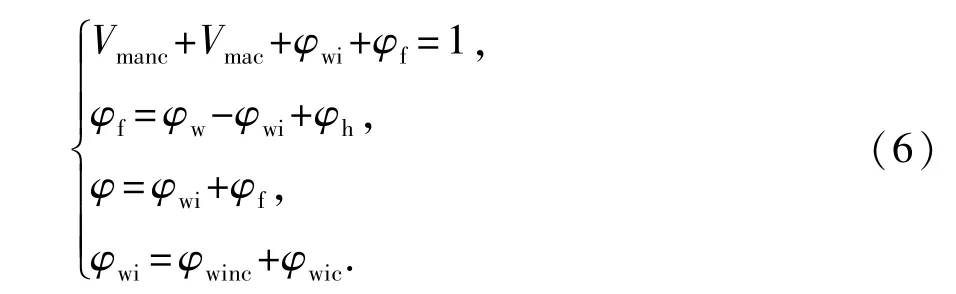
式中,Vmanc、Vmac分别为骨架导电纯岩石的不导电骨架颗粒、导电骨架颗粒的体积分数;φwi、φf分别为骨架导电纯岩石的束缚水孔隙度、自由流体孔隙度; φwinc、φwic分别为骨架导电纯岩石的不导电骨架相和导电骨架相相应的束缚水孔隙度;φw、φh分别为骨架导电纯岩石的含水孔隙度、含油气孔隙度;φ为骨架导电纯岩石的有效孔隙度。
假定不导电骨架颗粒与导电骨架颗粒大小相近,则φwinc和φwic计算公式为
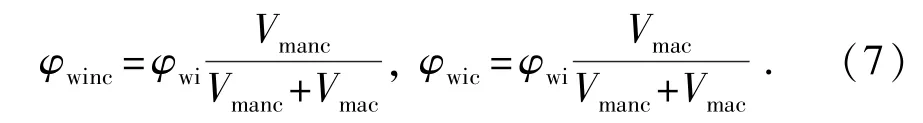
认为自由水和束缚水电导率相同,均为地层水电导率[22]。由于连通导电方程适用于描述只有一个导电相存在的两相混合介质的导电规律,而HB方程可以描述两相均导电或不导电的混合介质的导电规律,因此不导电骨架相和自由流体相的导电规律可用连通导电方程描述,而导电骨架相的导电规律必须用HB方程描述。对于不导电骨架相和自由流体相,可认为其中的水是完全连通的,即各相的水连通校正系数等于零,应用连通导电方程可得各相电导率为

图4 骨架导电纯岩石电阻率模型的体积模型Fig.4 Volume model of resistivity model for matrix-conducting clean sands

式中,σmancp、σf分别为不导电骨架相和自由流体相的电导率,S/m;φ′winc、φ′wf分别为不导电骨架相和自由流体相的相对含水体积分数;μs和μ分别为不导电骨架相和自由流体相的导电指数。
根据地层体积模型和各导电相相对含水体积分数的定义,可得
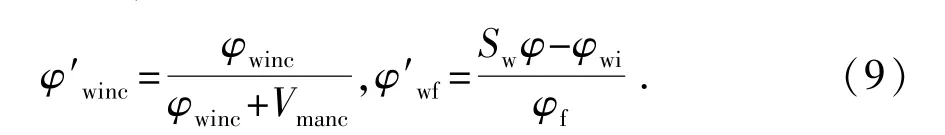
将式(9)代入式(8),可得
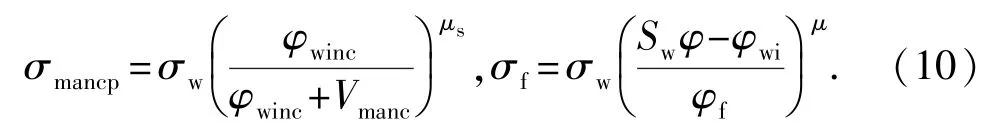
对导电骨架相应用HB方程得出导电骨架相电导率的表达式为

式中,σma为导电骨架颗粒的电导率,S/m;σmacp为导电骨架相电导率,S/m;mma为导电骨架颗粒的胶结指数。
对式(11)采用迭代方法求解,可求出σmacp。
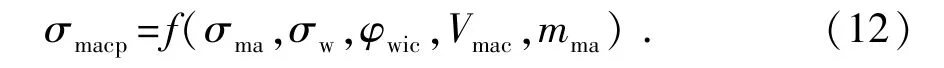
假设σt为岩石总电导率,Xmancp、Xmacp和Xf分别为不导电骨架相、导电骨架相和自由流体相的体积分数,根据混合导电定律[23]得


方程(16)即为基于连通导电理论和HB方程的骨架导电纯岩石电阻率模型。
3 模型的理论验证
3.1 边界条件
由式(16)和地层因素定义式,可得地层因素表达式为

由式(16)和电阻增大系数定义式,可得电阻增大系数表达式为

(1)当φ=1时,即岩石完全由孔隙组成,不含任何颗粒成分,则有Vmanc=0,Vmac=0。将Vmac=0代入式(11)可得σmacp=σw。将上述结果代入Xw表达式,则有

将φ=1和Xw=0代入式(17),可得出F=1,与按照F定义在φ=1情况下F==1.0相符。
(2)当Sw=1时,即岩石孔隙完全被水饱和。将Sw=1代入式(18),可得出I=1,与按照I定义在Sw=1情况下I==1.0相符。
在已有的文献中,通常将里根执政时期视为美国经济向自由化转折的时期,从经济学说的转变来看,这样的判断无疑是正确的。因为,在里根执政的80年代,不仅现代货币主义主导了美国的紧缩性货币政策实施,同时供给学派的减税主张也得到了实践的机会,最为重要的是沃克在担任美联储主席时在治理通胀时运用了理性预期学派的观点,确立了理性预期学派在西方宏观经济学中的地位,以上三个学派的学说共同支撑了新古典宏观经济学的理论体系。如果更准确地说,里根时期已经是新古典经济学确立其西方经济学主流地位的时期,而在此之后,特别是1998年东亚危机之后,新古典经济学的政策所带来的全球治理问题日趋严重,保护主义势力开始重新抬头。
(3)当φ=0时,即岩石完全由不导电颗粒和导电颗粒组成,不含孔隙,则有φwinc=0,φwic=0,φf=0。将φwic=0代入式(11)可得σmacp=σma,将上述结果代入式(15)可得

当Vmac=1.0时,即岩石完全由导电颗粒组成,且不含孔隙,则由式(21)可得σt=σmac,与实际相符。当Vmac=0时,即岩石完全由不导电颗粒组成,且不含孔隙,则由式(21)可得σt=0,与实际相符。
(4)当σw=σma,Vmanc=0,φf=φ-φwi时,即岩石由导电颗粒和孔隙组成,且孔隙完全含水,则有φwinc=0,φwic=φwi。将σw=σma代入式(11),可得σmacp= σma。将φwinc=0,φwic=φwi代入式(14),可得Xmancp= 0,Xmacp=Vmac+φwi,Xf=φ-φwi。将上述结果代入式(13),可得σt=σw,与实际相符。
3.2 理论分析
在束缚水饱和度Swi=0.25,φ=0.13,mmac= 2.0,μ=1.63,μs=1.4条件下,利用方程(16)对骨架导电纯岩石导电规律进行理论分析。
3.2.1 地层因素与孔隙度关系
对于骨架完全或部分由导电颗粒组成的岩石,假设Vmanc=0,σma=0.03 S/m或Vmac=0.1,σma= 0.83 S/m。图5给出了不同地层水电导率的F与φ交会图,从图中看出F随σw减小而减小。
综上,预测的骨架导电纯岩石地层因素与孔隙度的理论关系与实验规律相符,说明方程(16)能描述饱含水骨架导电纯岩石的导电规律。
3.2.2 地层电阻增大系数与含水饱和度关系
对于骨架完全或部分由导电颗粒组成的岩石,假设Vmanc=0,σma=0.03 S/m或Vmac=0.165,σma= 0.83 S/m。图7给出了不同地层水电导率的I与Sw交会图,从图中看出I随σw减小而降低。
对于骨架由部分导电颗粒组成的岩石,假设σma=2.5 S/m,σw=1.89 S/m,图8(a)给出了不同导电骨架颗粒体积分数的I与Sw交会图,从图中看出,I随Vmac增大而减小。假设Vmac=0.1,σw=2.08 S/m,图8(b)给出了不同导电骨架颗粒电阻率的I与Sw交会图,从图中看出I随ρmac减小而降低。
综上所述,方程(16)预测的骨架导电纯岩石电阻增大系数与含水饱和度的理论关系与实验规律相符,由此说明方程(16)能描述含油气骨架导电纯岩石的导电规律。
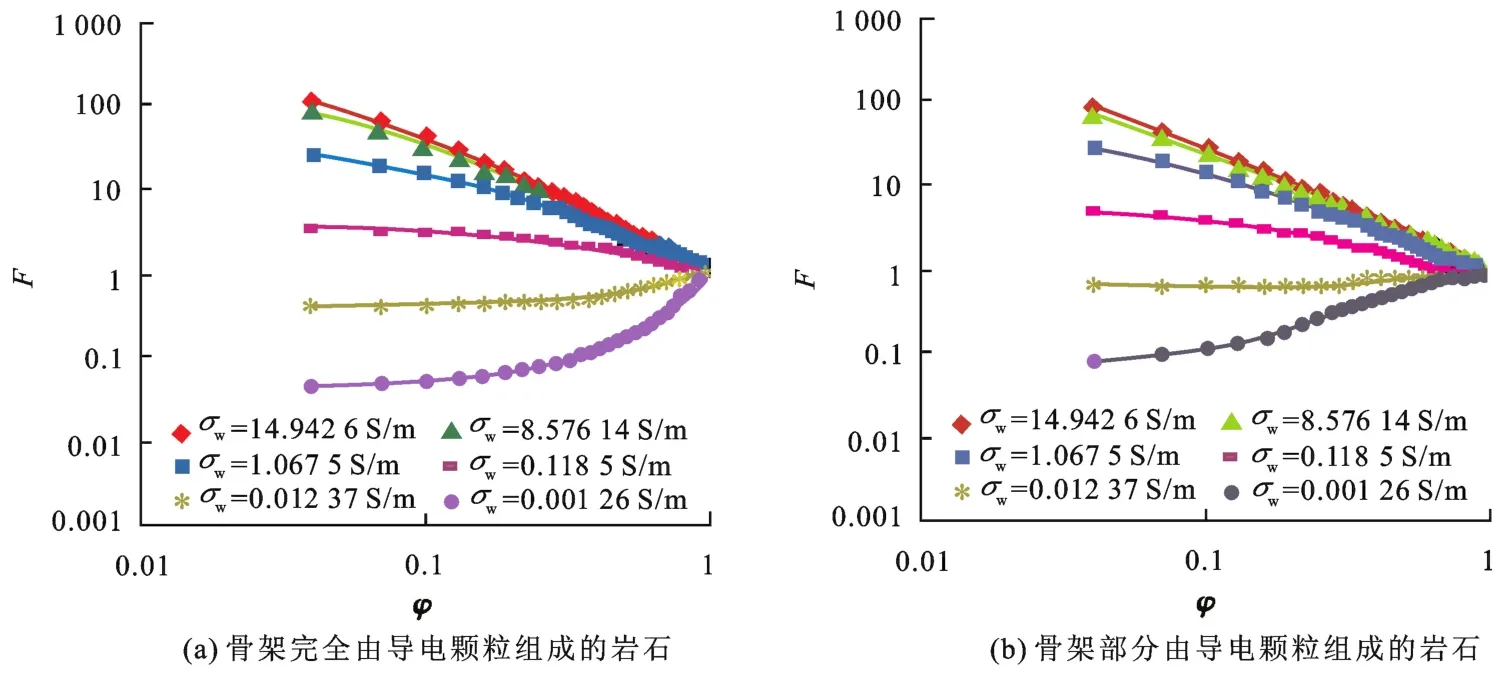
图5 不同地层水电导率的F与φ理论关系Fig.5 Theoretical relationships between F and φ for different σw
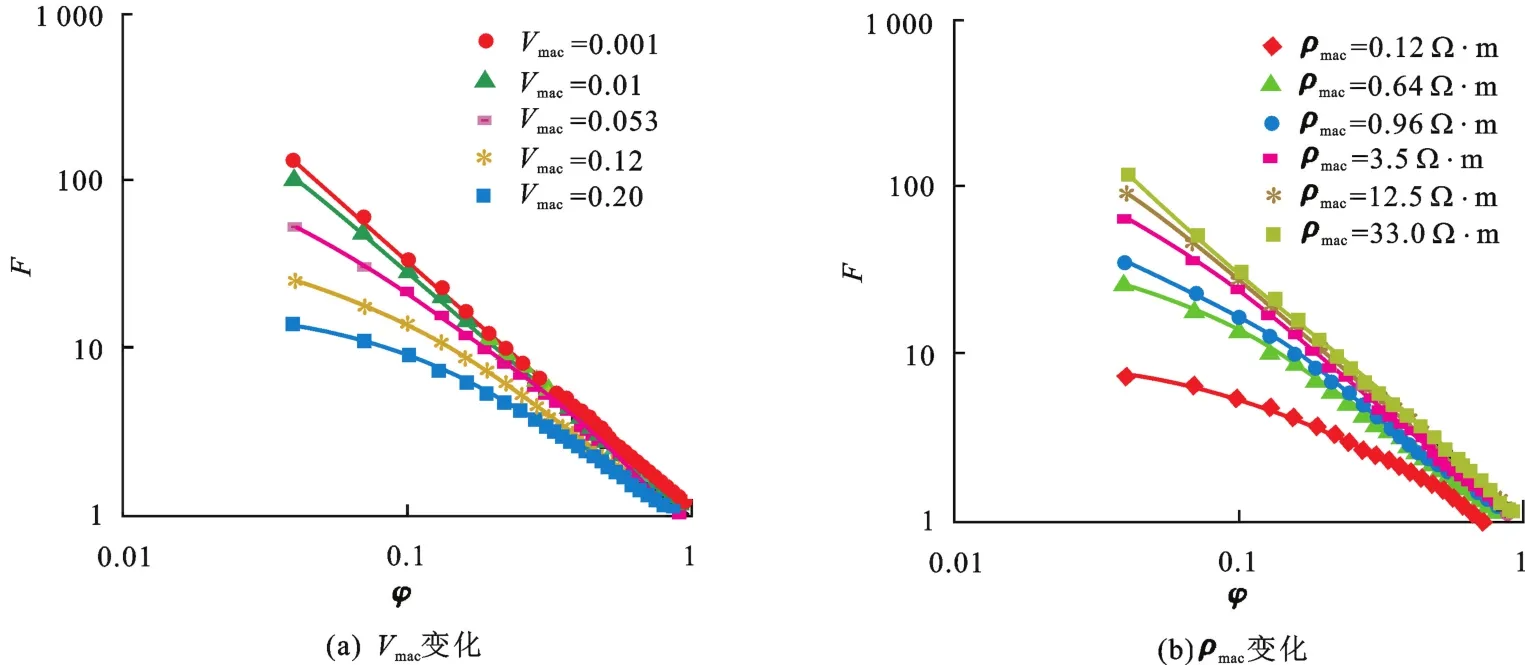
图6 骨架部分由导电颗粒组成岩石的F与φ理论关系Fig.6 Theoretical relationships between F and φ of sands with matrix composed partially of conductive grains

图7 不同地层水电导率的I与Sw理论关系Fig.7 Theoretical relationships between I and Swfor different σw

图8 骨架部分由导电颗粒组成岩石的I与Sw理论关系Fig.8 Theoretical relationships between I and Swof sands with matrix composed partially of conductive grains
4 模型的实验验证
4.1 骨架完全由导电颗粒组成的岩样
对于10块骨架完全由导电颗粒组成的人造岩样[14],有Vmanc=0.0,φwinc=0.0,φwic=φwi,利用最优化技术求解σo-σw的非相关函数,可优化得到模型中各未知参数值(表1)。从表中可以看出,对于该组骨架完全由导电矿物组成的岩样,计算的导电骨架颗粒电阻率为27.5~39.3 Ω·m,均值为32.83 Ω·m,与真值32.47 Ω·m非常接近。图9给出了利用优化的各参数值骨架导电纯岩石电阻率模型计算该组岩样的电导率值与岩心测量值对比图(其中符号点为岩心测量数据,曲线为方程计算结果),从图中可以看到曲线与符号点的一致性很好,说明本文建立的骨架导电纯岩石电阻率模型能描述骨架完全由导电矿物组成的含水纯岩石的导电规律。
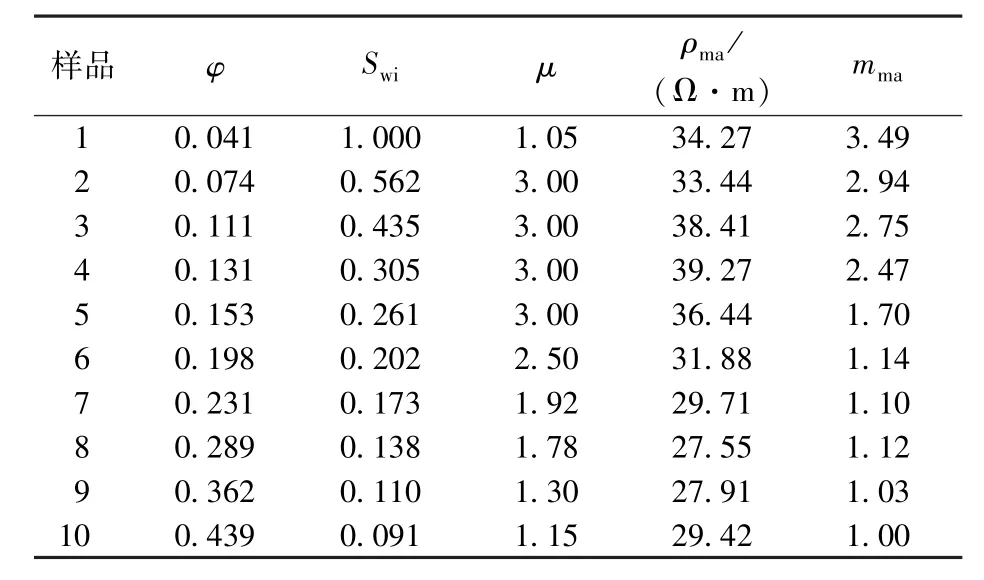
表1 骨架完全由导电颗粒组成的人造岩样的电阻率模型优化参数Table 1 Optimization parameters of resistivity model for artificial samples with matrix composed entirely of conductive grains

图9 计算骨架完全由导电颗粒组成岩样电导率值与实验测量值对比Fig.9 Comparison of calculated conductivity with measured conductivity for samples with matrix composed entirely of conductive grains
4.2 骨架部分由导电颗粒组成的岩样
对于10块黄铁矿体积分数不同的全直径砾岩岩样[4],利用最优化技术求解σo-σw的非相关函数,可优化得到模型中各未知参数值,图10给出了利用优化的各参数值方程计算该组岩样的电导率值与岩心测量值对比图(以频率35 Hz的为例,其中符号点为岩心测量数据,曲线为方程计算结果),从图中可以看到曲线与符号点的一致性很好,这说明建立的骨架导电纯岩石电阻率模型能描述骨架含一定量导电矿物的含水纯岩石的导电规律。

图10 计算骨架部分由导电颗粒组成岩样电导率值与实验测量值对比Fig.10 Comparison of calculated conductivity with measured conductivity for samples with matrix composed partially of conductive grains
5 结 论
(1)骨架导电纯岩石的地层因素值与孔隙度在双对数坐标上为非线性关系。当骨架电阻率大于水电阻率时,地层因素值大于1.0,而当骨架电阻率小于水电阻率时,地层因素值小于1.0。随水电导率增大,地层因素值增大。随导电颗粒体积分数和电导率增大,地层因素值降低。
(2)骨架导电纯岩石的电阻增大系数与含水饱和度在双对数坐标上为非线性关系,无论骨架电阻率大于或小于水电阻率,电阻增大系数均大于1.0。随水电导率减小,电阻增大系数减小。随导电颗粒体积分数和电导率增大,电阻增大系数降低。
(3)建立的骨架导电纯岩石电阻率模型满足一定边界条件:①当孔隙度为100%时,地层因素值等于1;②当含水饱和度为100%时,电阻增大系数等于1;③当孔隙度为0%,导电颗粒体积分数为100%时,岩石电导率等于导电颗粒电导率,而当孔隙度为0%,导电颗粒体积分数为0%时,岩石电导率等于0;④当岩石由导电颗粒和饱含水孔隙组成,且水电导率等于导电颗粒电导率时,岩石电导率等于水电导率。
(4)新建立的模型既能描述骨架完全由导电矿物组成的纯岩石导电规律,又能描述骨架含一定量导电矿物的纯岩石导电规律,适用范围更广,可用于定量评价骨架导电低阻油层的饱和度。
[1] 宋帆,李华玮,蒋智格.塔里木盆地低电阻率油层识别及饱和度计算技术[J].国外测井技术,2003,18(3): 25-29.
SONG Fan,LI Huawei,JIANG Zhige.Identification method and calculation technology of saturation for low resistivity reservoirs in Tarim Basin[J].World Well Logging Technology,2003,18(3):25-29.
[2] 中国石油勘探与生产公司.低阻油气藏测井识别评价方法与技术[M].北京:石油工业出版社,2006.
[3] 李浩,刘双莲.港东东营组低电阻油层解释方法研究[J].断块油气田,2000,7(1):27-30.
LI Hao,LIU Shuanglian.Interpretation method for low resistivity reservoir in Dongying formation in the east of Dagang Oilfield[J].Fault-Block Oil&Gas Field,2000, 7(1):27-30.
[4] CLAVIER C,HEIM A,SCALA C.Effect of pyrite on resistivity and other logging measurements[C/OL]//The SPWLA 17th Annual Logging Symposium.Colorado, 1976,Paper HH[1976-06-09].https://www.onepetro.org/conference-paper/SPWLA-1976-HH.
[5] CLENNELL M B,JOSH M,ESTEBAN L,et al.The influence of pyrite on rock electrical properties:a case study from NW Australian gas reservoirs[C/OL]//The SPWLA 51th Annual Logging Symposium.Austrilia, 2010,PaperUUU[2010-06-19].https://www.onepetro.org/conference-paper/SPWLA-2010-97081.
[6] GIVENS W W,SCHMIDT E J.A generic electrical con-duction model for low-contrast resistivity sandstones[C/ OL]//The SPWLA 29th Annual Logging Symposium.Texas,1988,Paper E[1988-06-05].https://www.onepetro.org/conference-paper/SPWLA-1988-E.
[7] GIVENS W W.A conductive rock matrix model(CRMM) for the analysis of low-contrast resistivity formations[J].The Log Analyst,March-April,1987:138-164.
[8] WU P Y,HSIEH B Z,CHILINGAR G V,et al.Estimation of water saturation in rocks with conductive matrix [J].Energy Sources,Part A:Recovery,Utilization, and Environmental Effects,2008,30(5):401-410.
[9] 宋延杰,吕桂友,王春燕,等.混合泥质砂岩有效介质通用HB电阻率模型研究[J].石油地球物理勘探, 2003,38(3):275-280.
SONG Yanjie,LÜ Guiyou,WANG Chunyan,et al.Study of general effective medium HB model in mixed shaly sands[J].Oil Geophysical Prospecting,2003,38 (3):275-280.
[10] SONG Yanjie,WANG Xiuming,LU Shuangfang.A generalized equivalent resistivity model in laminated and dispersed shaly sands[J].Exploration Geophysics,2005,36(2):245-250.
[11] 宋延杰,王秀明,卢双舫.骨架导电的混合泥质砂岩通用孔隙结合电阻率模型研究[J].地球物理学进展,2005,20(3):747-756.
SONG Yanjie,WANG Xiuming,LU Shuangfang.Generalized matrix-conducting pore combination resistivity model in laminated and dispersed shaly sands[J].Progress in Geophysics,2005,20(3):747-756.
[12] 宋延杰,唐晓敏.低阻油层通用有效介质电阻率模型[J].中国科学:D辑,2008,38(7):896-909.
SONG Yanjie,TANG Xiaomin.The generalized symmetrical effective medium resistivity model for low resistivity reservoir[J].Science in China(Series D):Earth Sciences,51(8):1179-1193.
[13] 陈科贵,罗兵,郭睿,等.中东某油田低阻油层含水饱和度计算方法探讨[J].石油天然气学报,2012,34 (6):57-60.
CHEN Kegui,LUO Bing,GUO Rui,et al.Method for calculating water saturation in low resistivity reservoirs of an oil field in Middle East[J].Journal of Oil and Gas Technology,2012,34(6):57-60.
[14] GLOVER P W J,HOLE M J,POUS J.A modified Archie's law for two conducting phases[J].Earth and Planetary Science Letters,2000,180:369-383.
[15] GLOVER P W J.A generalized Archie's law for n phases[J].Geophysics,2010,75(6):E247-E265.
[16] MONTARON B.Fractals,percolation theory and the stability of Archine's‘m’exponent:The SPWLA Topical Conference on“Low Resistivity Pay in Carbonates”,UAE,2005[C].UAE:AbuDhabi,c2005.
[17] MONTARON B.A quantitative model for the effect of wettability on the conductivity of porous rocks[R].SPE 105041,2007.
[18] MONTARON B.Connectivity theory—a new approach to modeling non-Archie rocks[J].Petrophysics,2009,50 (2):102-115.
[19] MONTARON B.A connectivity model for the electrical conductivity of sandstone rocks[C/OL]//The SPWLA 50th Annual Logging Symposium.Texas,2009[2009-06-21].https://www.onepetro.org/conference-paper/ SPWLA-2009-58516.
[20] HANAI T.Theory or the dielectric dispersion due to the interfacial polarization and its application to emulsions [J].Kolloiod-Zeitschrift,1960,171:23-31.
[21] HANAI T.A remark on“Theory of the dielectric dispersion due to the interfacial polarization and its application to emulsions”[J].Kolloiod-Zeitschrift,1960,175:61-62.
[22] 宋延杰,么丽娜,徐广田,等.长垣地区低孔隙度低渗透率砂岩储层中连通导电模型的应用[J].测井技术,2012,36(4):345-351.
SONG Yanjie,YAO Lina,XU Guangtian,et al.Study on connectivity model for low porosity and permeability sand reservoirs in Daqing placanticline[J].Logging Technology,2012,36(4):345-351.
[23] TENCHOY G G.Evaluation of electrical conductivity of shaly sands using the theory of mixtures[J].Journal of Petroleum Science and Engineering,1998,21:263-371.
(编辑 修荣荣)
Matrix-conducting resistivity model for clean sands based on connectivity conductance theory and HB equation
SONG Yanjie1,2,LI Xiaojiao1,TANG Xiaomin1,2,FU Jian1
(1.College of Geoscience,Northeast Petroleum University,Daqing 163318,China; 2.Accumulation and Development of Unconventional Oil and Gas,State Key Laboratory Cultivation Base Jointly-constructed by Heilongjiang Province and Ministry of Science and Technology,Daqing 163318,China)
Most of the commonly used resistivity models are unable to give a precise description of conductive laws of sands whose rock matrix contains a certain amount of pyrite,therefore it is necessary to study the conductive laws and to propose a matrix-conducting resistivity model.The effects of water resistivity and conductive matrix grain content in matrix-conducting clean sands are first analyzed by using laboratory resistivity measurements of artificial and field samples,in which the rock matrix is composed partially or entirely of conductive grains.The results shown in a log-log graph suggest nonlinear relationships between formation resistivity factor and porosity,and between formation resistivity index and water saturation,respectively.Values of the formation resistivity factor and the index decrease with decreasing water conductivity,or increasing conductive matrix grain content.Second,based on the compositions of matrix-conducting clean sands and the characteristics of connectivitySONG Yanjie,LI Xiaojiao,TANG Xiaomin,et al.Matrix-conducting resistivity model for clean sands based on connectivity conductance theory and HB equation[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38 (5):66-74.conductance theory,matrix-conducting clean sands are divided into non-conducting matrix phase,conductive matrix phase and free fluid phase.Since the connectivity conductance equation applies to only one conducting composition and one non-conducting composition,while the HB equation can describe systems of two conducting compositions,a new matrix-conducting resistivity model for clean sands is proposed combining the connectivity conductance theory and the HB equation.The results show that the theoretical relationships between formation resistivity factor and porosity,and between formation resistivity index and water saturation predicted by the proposed model are consistent with the experimental values,and the proposed model is in compliance with meaningful physical bounds.The matrix-conducting resistivity model for clean sands can describe the conductive law of matrix-conducting clean sands,in which rock matrix is composed entirely or partially of conductive grains.The proposed model can be applied to quantitatively calculate saturation in matrix-conducting low resistivity reservoirs.
clean sand;pyrite;connectivity conductance theory;HB equation;resistivity model
P 631.84
A
1673-5005(2014)05-0066-09
10.3969/j.issn.1673-5005.2014.05.009
2014-02-21
国家自然科学基金项目(41274110)
宋延杰(1963-),男,教授,博士,主要从事测井方法与资料解释研究。E-mail:syj1963@263.net。
宋延杰,李晓娇,唐晓敏,等.基于连通导电理论和HB方程的骨架导电纯岩石电阻率模型[J].中国石油大学学报:自然科学版,2014,38(5):66-74.

