带航路规划的反舰导弹禁区计算方法研究*

刘宗杰 王天辉 宋贵宝

(1.91851部队 葫芦岛 125001)(2.海军航空工程学院飞行器工程系 烟台 264001)

带航路规划的反舰导弹禁区计算方法研究*

刘宗杰1王天辉1宋贵宝2

(1.91851部队 葫芦岛 125001)(2.海军航空工程学院飞行器工程系 烟台 264001)

针对带航路规划的反舰导弹禁区难计算的问题,在分析了影响禁区主要因素和航路规划反舰导弹的弹道特性的基础上,建立了直线弹道禁区、弯道禁区和雷达扫描禁区的计算模型。最后以某型反舰导弹为例对其禁区进行了计算,验证了模型的有效性,为带航路规划的反舰导弹的禁区计算提供了依据。

禁区; 航路规划; 反舰导弹; 影响因素

Class Number TP273+.5

1 引言

反舰导弹在飞行试验时,为保障海上过往船只、参演舰艇以及海上钻井平台等设施的安全,必须预先确定反舰导弹的飞行禁危区,其大小直接关系到扫海所投入的兵力和时间。而禁区是计算危险区的基础,科学合理地划定禁区,能够高效地利用扫海兵力、缩短扫海时间。传统的禁危区的计算是将禁区的计算按反舰导弹的弹道特点进行划分,分为助推段、自控段和自导段[1～3]。而具有航路规划的反舰导弹的自控段弹道不同于其他反舰导弹,其弹道具有灵活多变的特点,同时也带来了禁区难以计算的问题。

为了解决带航路规划的反舰禁区计算难的问题,在详细分析带航路规划反舰导弹弹道特点和导弹飞行过程中受到的影响因素的基础上,将禁区的计算划分为直线弹道禁区、弯道禁区和雷达扫描禁区,从而针对具有特定航路的反舰导弹通过逐段禁区合成的方法来构成相应的禁区。

2 禁区影响因素分析计算

影响反舰导弹射击禁区划定的因素众多,本文从导弹的发射平台、风、气温和导弹的系统误差对导弹飞行误差的影响进行分析,并给出相应的误差计算公式。

2.1 风

风对导弹的影响可等效为导弹受到纵风和横风两个方向外力的共同作用。横风的作用是使导弹产生横向移动和绕其重心的转动,在横风的作用下使导弹在顺风方向上产生加速运动。导弹的横移速度由零逐渐增加到与横风速相等,然后导弹将以此横移速度随风漂移。纵风对导弹的作用只产生纵向上的平移运动,而不产生绕重心的转动[4～5]。

由此横风和纵风都将对导弹造成偏离,风对导弹的作用计算公式如式(1)：

EW=VW×TW

(1)

式中VW为导弹发射时的最大风速,TW为导弹飞行的时间。

2.2 气温

气温对导弹的发动机造成影响,其影响规律一般为气温升高,导弹速度变大,总飞行时间减少；气温降低,导弹速度变小,总飞行时间增加[4]。综合考虑可以用经验公式来描述气温变化和飞行时间的变化规律：

(2)

式中Δt为导弹飞行时间的变化量；a为系数；D为导弹飞行距离；ΔT为相对于发射点温度的变化值。

由此气温对纵向造成误差的计算公式如式(3)：

ET=V·Δt

(3)

2.3 发射平台

本文主要考虑水面平台的定位、定向和摇摆对导弹发射点和姿态的影响,由于舰船的摇荡对导弹姿态的影响在其发射后可以逐渐修正,在此不进行考虑,但是侧向偏移不能消除[4]。导弹的发射点的散布误差是在圆形区域内的散布,其误差半径为R0。

航向误差角造成的偏差为

Ea=V·Tasinφa

(4)

式中φa为导弹的航向误差角度,Ta为导弹的飞行时间。

温度变化造成导弹飞行的纵向偏差,而发射角度的偏差造成侧向偏差,可以将其转化为合成误差：

(5)

2.4 惯导误差

对于同一型导弹,飞行时间越长,惯导系统的误差就越大,累计误差则需要根据惯导系统的极限误差结合导弹飞行距离确定[4]。在此将导弹的极限误差转化为单位误差,则导弹飞行tS时间后误差计算如式(6)：

(6)

式中ESX和ESY分别为导弹在飞行结束后,由惯导引起的侧向和纵向的最大偏差,tmax为导弹的最大飞行时间。

3 带航路规划的反舰导弹典型弹道分析

具有航路规划的反舰导弹可以有效地规避敌方火力,绕过海岛,对躲避在海岛后面的敌方目标进行打击[6],其典型弹道如图1所示。

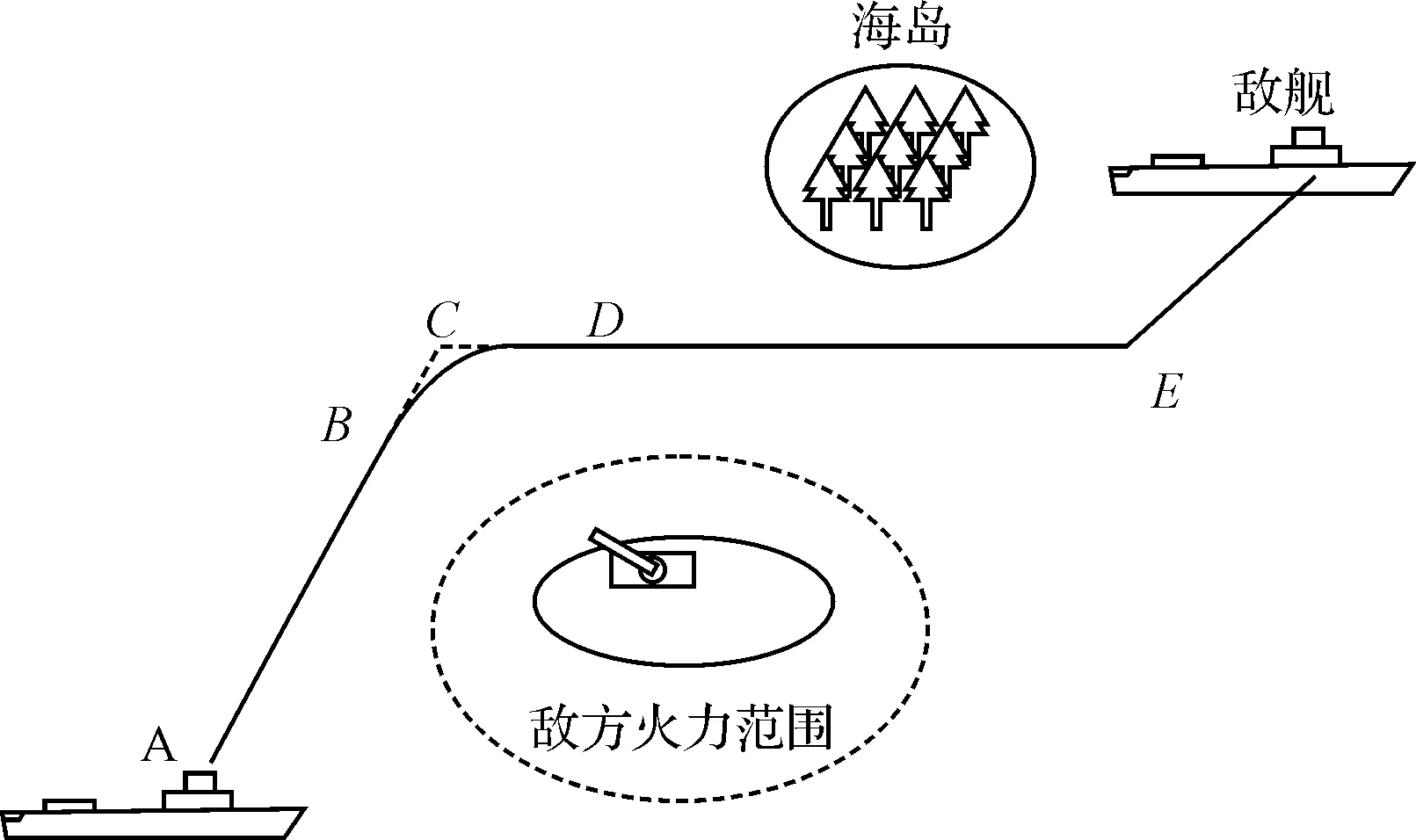
图1 航路规划示意图

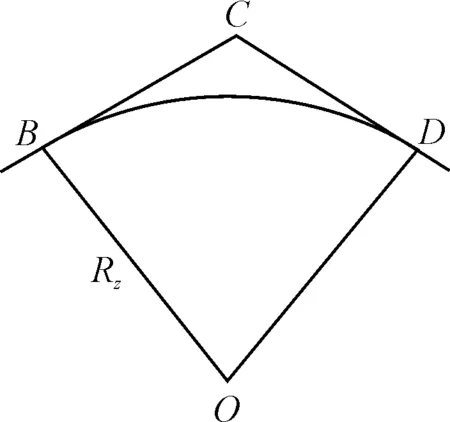
图2 航路规划的反舰导弹巡航转弯示意图

导弹在其规划航路上设置多个航路节点,一般按巡航级侧向弹道采用切点转弯方式来实现沿规划航路飞行,即导弹临近航路点之前就按预定的转弯半径实现转弯,当导弹的航向与预定的转弯航向一致后,转弯结束。以图1中的第一个航路点C进行说明,如图2所示,BC为导弹转弯前的飞行方向,CD为导弹转弯后的飞行方向,点C为导弹航路规划点,可见导弹并不能飞行到导弹航迹规划点C,弧线BD为导弹的按航迹规划点C的转弯弹道,RZ为转弯弧线弹道的半径。

4 禁区划分及计算

在禁区误差计算时由风造成的误差Ew可由式(1)计算得到,由温度和发射角度误差影响的弹道偏差EH可由式(5)计算得到,由系统误差引起的飞行偏差Es可根据式(6)计算获得。可以得到助推段和自控段各个端点的误差半径计算公式

RM=RC+Ew+EH+Es

(7)

对于自导段的误差的计算,由于此时导弹雷达已开机,导弹由自动控制改为自主导引,系统误差不再包含惯导误差,其误差半径的计算公式为：

RM=RC+Ew+EH

(8)

式(7)、(8)中RC为禁区初始点误差半径,RM为计算段末端误差半径。

由于带航路规划的反舰导弹禁区的计算不仅具有直线弹道禁区,还具有弯道禁区,下面分别进行讨论。为了计算的方便,以下将各个禁区的计算均建立在各自的坐标系,最后在禁区计算完毕后,需要通过坐标变换的方式转化到发射坐标系下。

4.1 直线弹道禁区

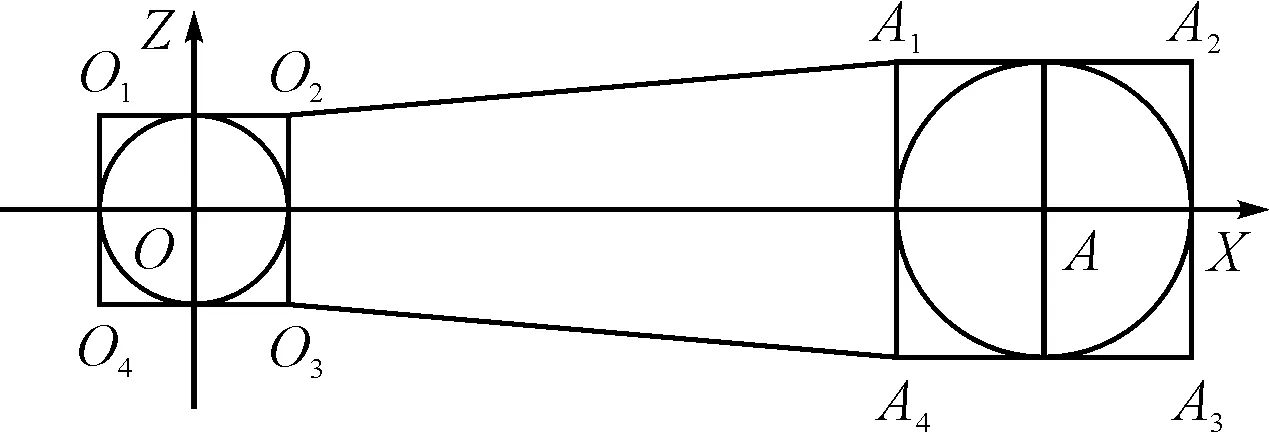
图3 直线段禁区计算示意图

直线弹道如图3所示,起点散布区域前向边界为O1(-XO,ZO),O4(-XO,-ZO),后向边界为O2(XO,ZO),O3(XO,-ZO),其中：

(9)

终点散布区域前向边界A1(XAR,ZAR),A4(XAR,-ZAR),其中：

(10)

终点散布区域后向边界A2(XAL,ZAL),A3(XAL,-ZAL),其中：

(11)

式(9)～式(11)均建立在O坐标系下,其中R0为初始点散布误差半径,RA为终点散布误差半径。

4.2 弯道禁区

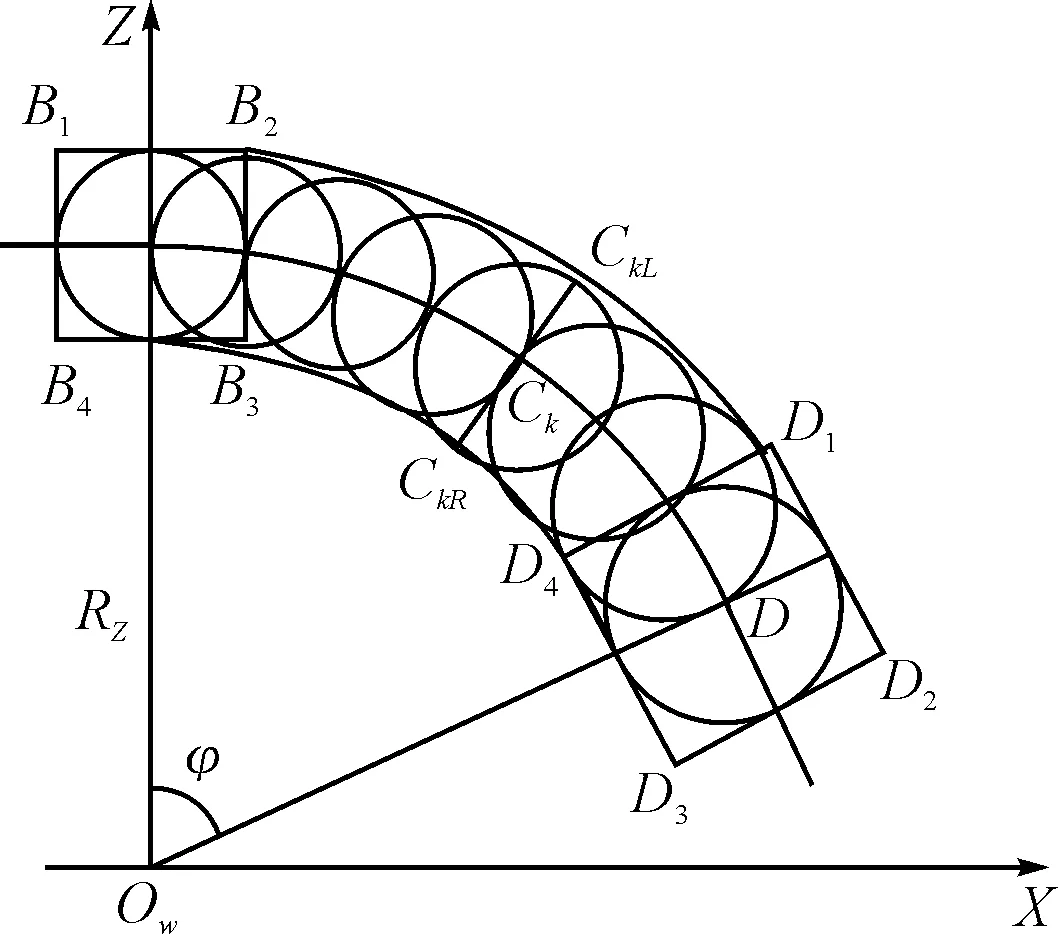
图4 弯道禁区示意图

由于导弹在某点圆形散布区域的计算是根据各种因素对时间的累积误差,计算该圆形区域首先要知道导弹飞到该点所用的时间,然后算得各种因素在该点的累积误差,得到该点圆形区域的散布半径。因为无法计算出弯道上每一个点的圆形散布区域,所以采用对弯道进行逐段进行计算的方法,然后连接每段的禁区的边界点,相信在对弯道分段不断加细的过程中可以划定出可靠的禁区。

弯道禁区如图4所示,根据转弯弹道的长度将其等分为n段,等分点为ik(k=0,1,2,…,n),其中B点即为i0点,D点即为in点。

B点散布区域前向边界端点位置为B1(XBL,ZBU),B4(XBL,ZBD),后向边界端点位置为B2(XBR,ZBU),B3(XBR,ZBD),其中：

(12)

导弹转弯转过的角度为φ,转弯半径为Rz,根据导弹的平均速度,可以计算得到当导弹转弯到Ck点时转过的角度φk和导弹飞行的误差半径RCk。由此可以计算Ck点的左右两侧散布边界点CkR(XCkR,ZCkR),CkL(XCkL,ZCkL),其中：

(13)

式(12)、(13)是建立在坐标系OW中进行的计算。

D点为转弯结束时直线弹道的启示点,可以在其坐标系中计算边界点。

4.3 雷达搜索禁区

反舰导弹末制导雷达的搜索区是一个扇形的空间区域,其范围大小由最大搜索角和作用距离共同决定。这一区域是反舰导弹射击禁区的主要组成部分,同时也是对目标威胁最大的区域[4]。

设为导弹末制导雷达航向最大搜索角为α,最大搜索距离为l1,雷达开机后,导弹飞行的距离为l2。

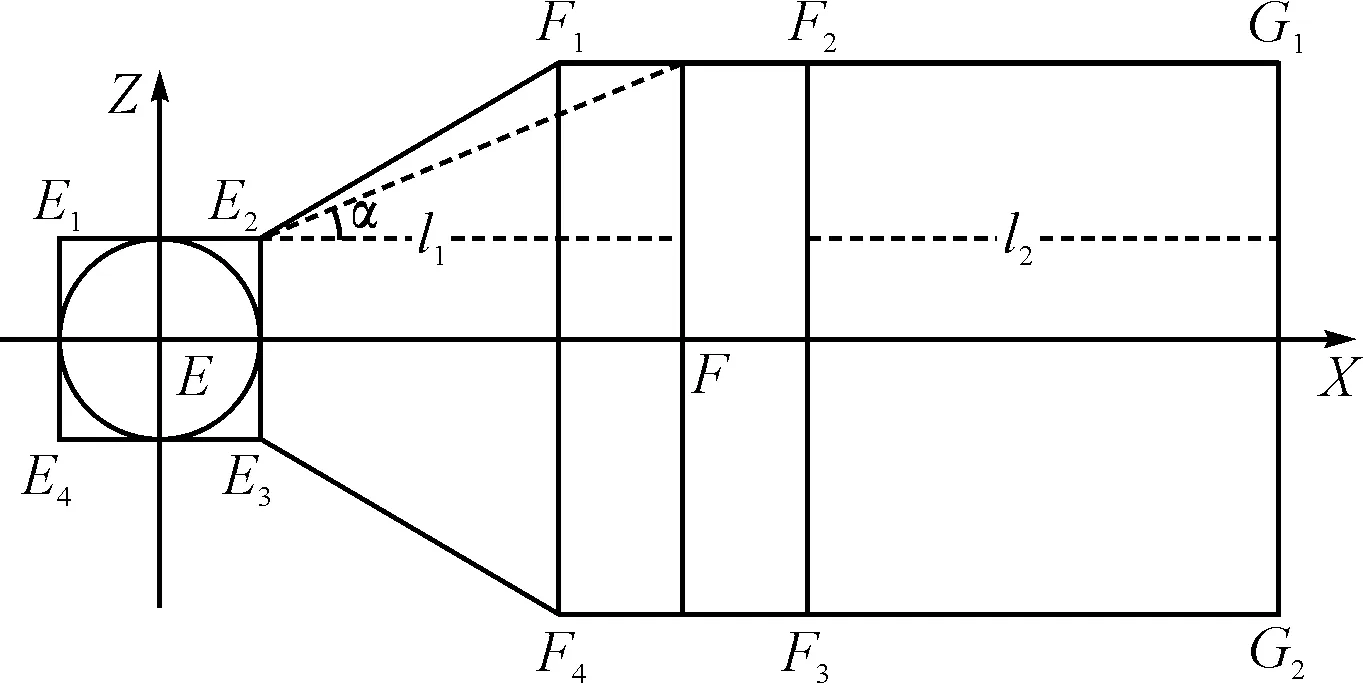
图5 雷达扫描禁区示意图

由于此时导弹的末制导雷达已经开机,其侧向边界将扩大,所以其终点散布不再是规则的圆形区域,散布区域包线为矩形区域。

E点散布区域前向边界端点坐标为E1(-XE,ZE),E4(-XE,-ZE),后向边界端点坐标为E2(XE,ZE),E3(XE,-ZE),其中：

(14)

末端雷达扫描区域前向边界端点坐标为F1(XFL,ZEL),F4(XE,-ZE),其中：

(15)

末端雷达扫描区域后向边界端点坐标为G1(XG,ZG),G2(XG,-ZG),其中：

(16)

式(14)～式(16)是以E为坐标原点建立的坐标系下进行的计算,其中RE为E点散布误差半径,RF为导弹径直飞行时F点散布误差半径。

5 计算实例

为了验证模型,以某型带航路规划的反舰导弹为例进行计算。导弹的平均飞行速度为300m/s,发射平台的初始散布误差半径为500m,初始风速为10m/s,导弹经发射后飞行60km后,到达第一个航路规划点,向右转弯25°,继续飞行50km,到达第二个航路规划点,向右转弯35°,继续飞行40km,到达第三个航路规划点,向右转弯30°,继续沿直线飞行24km后,末制导雷达开机,导弹进入自导段,雷达扫描角度15°,雷达扫描远界15km,最后飞行15km,根据第4节的计算模型由Matlab仿真得到禁区图形,如图6所示。

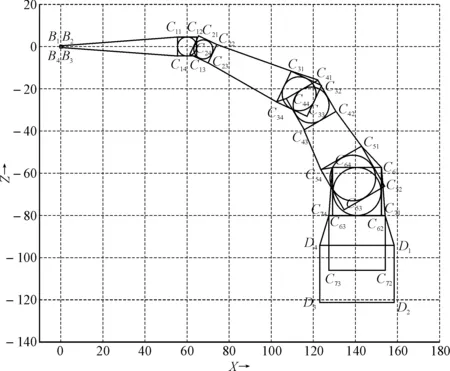
图6 某型反舰导弹禁区计算示意图

由B1、B2、B3和B4围成初始点散布区域,经三次转弯,导弹到达自控段终点,其散布区域由C71、C72、C73和C74围成,然后雷达开机,雷达扫描区域由D1、D2、D3和D4围成。

6 结语

在仿真实例中为了简化计算同时在不影响说明问题的情况下以导弹的平均速度进行了计算,不够严谨。如果通过弹道仿真的方法来计算导弹到达各个端点的时间相信能够得到更加精确的禁区图形。本文建立直线弹道禁区、弯道禁区和雷达扫描禁区的计算模型可以应用于具有特定航路的反舰导弹的禁区计算中,根据相应的弹道可以灵活合理地将各个模型进行组合。

[1] 姜立涛,杨和.反舰导弹飞行禁区危险区的计算方法[J].海上靶场学术,2007(4):10-13.

[2] 李翼,钟生新,童幼堂.舰舰导弹禁危区计算[J].战术导弹技术,2004(3):33-35.

[3] 焦吉祥.某型潜射反舰导弹射击禁区和危险区的界定[J].潜艇学术研究,2007,25(4):44-45.

[4] 宋贵宝,刘宗杰,王作祥.反舰导弹禁危区划定影响因素分析[J].战术导弹技术,2012,(5):24-29.

[5] 李永胜,许诚,王伟力,等.一种划定反舰导弹飞行航区的设计与实现[J].飞行力学,2009,25(1):55-58.

[6] 王于臣,康晓予,王宁宁.航路规划在反舰导弹打击岛礁附近目标的应用[J].舰船电子工程,2013,33(6):32-34.

[7] 刘刚,陈国生,老松杨,等.反舰导弹航路规划与几何特征及规律[J].电光与控制,2013,20(9):23-27.

[8] 李圣杰,周智超,寇红超.舰路规划反舰导弹对海军合同对海攻击战术与影响[J].舰船电子工程,2012,32(5):1-3.

Forbidden Zone for Anti-ship Missile with Path Planning Capability

LIU Zongjie1WANG Tianhui1SONG Guibao2

(1. No. 91851 Troops of PLA, Huludao 125001) (2. Department of Airborne Vehicle Engineering, Naval Aeronautical and Astronautical University, Yantai 264001)

Aiming at the difficulty in calculating the forbidden zone of anti-ship missle with path planning capability, based on the analysis of factors affecting forbidden zone and features of trajectory, the forbidden calculating model of straight trajectory, curved trajectory and radar scanning is built. At last, a type of anti-ship missle’s forbidden zone is taken as an example to calculate its forbidden zone to verify the proposed model’s effectiveness, and provide basis for forbidden zone calculating of anti-ship missle with path planning.

forbidden zone, path planning, anti-ship missile, influence factor

2014年6月8日,

2014年7月27日

刘宗杰,男,硕士,助理工程师,研究方向:导弹系统工程。

TP273+.5

10.3969/j.issn1672-9730.2014.12.011