足式机器人单腿跳跃仿真与实验
钟建锋,罗 欣,余益君
(华中科技大学数字制造装备与技术国家重点实验室,湖北 武汉430074)
0 引言
在非连续的地面环境下,相比于轮式、履带式机器人,足式移动机器人显示出更强的灵活性和环境适应能力。跳跃运动是四足动物实现快速移动和跨越障碍的典型运动方式,也是高性能四足机器人运动能力期望达到的目标。在结构设计方面,现有的跳跃机器人大多都采用仿生结构,充分利用这种自然选择的动物结构形式[1-3]。国内的学者在仿青蛙跳跃机器人和仿袋鼠跳跃机器人领域也取得了一些研究成果[4-5]。跳跃过程是一个需瞬时大量供能的动态过程,传统的电机驱动方式的瞬间出力能力不能满足要求,高能量密度的液压驱动凭借高负载能力和抗冲击等优点成为大多数机器人的选择。目前,具备户外载重自主运动能力的最具代表性的足式机器人[6-8]等均采用液压驱动。
机器人跳跃的主要控制方法有基于SLIP模型的控制方法[9]和基于位置跟踪的控制方法。在此,以四足机器人单腿为研究载体,开展跳跃运动研究。
1 单腿竖直跳跃运动模型
机器人单腿构型设计如图1所示。对于四足机器人单腿的竖直跳跃运动,只关注矢状面上的运动特性,而侧向运动不予考虑。因此,可将单腿视为一个平面多刚体系统,即将机器人髋部、大腿和小腿等效为具有质量的平面刚性连杆。单腿连续跳跃时,根据足尖是否脱离地面,可分为着地相和飞行相2个阶段,腿末端在着地(着地相)和飞行(飞行相)2种状态间交替切换,腿末端着地时,腿部运动受到地面的约束。腿末端腾空时,腿部与地面的约束解除,腿部不再受外部作用力和力矩。
小腿、大腿和髋部的质量、转动惯量和长度分别记为 m1,J1,l1,m2,J2,l2和 m3,J3,l3。小腿质心到末端的距离记为,到膝关节的距离记为,显然有+=l1,同理,大腿质心到膝关节的距离记为,到髋关节的距离记为,有+=l2。髋部质心到髋关节的距离记为lm3。小腿末端的弹簧刚度记为k,由于实际使用的弹簧刚度较大,可以忽略弹簧压缩对小腿质心位置的影响。
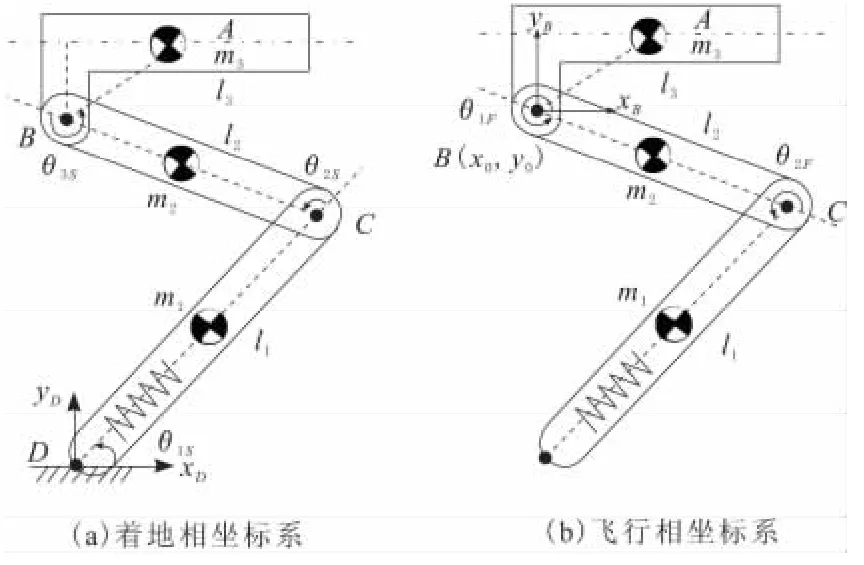
图1 着地相和飞行相坐标系
1.1 着地相运动学和动力学
机器人跳跃过程中的上升起跳和下降压缩阶段均处于着地相,其运动方程是一致的。在如图1a所示的着地相中,以足端着地点D为原点,建立局部坐标系xDDyD。在关节空间下,[θ1S,θ2S,θ3S]描述了腿部的绝对姿态,其中,小腿与地面夹角θ1S为被动关节,膝关节θ2S和髋关节θ3S为驱动关节。
假设机器人单腿处于着地相时,腿部末端与地面接触,且不与地面发生滑移,则腿末端与地面的约束可视为铰接运动副约束。选取着地相广义坐标为θS=[θ1S,θ2S,θ3S]T。
根据 Denavit-Hartenberg(D-H)法,单腿各部分质心位置在着地相坐标系下分别为:
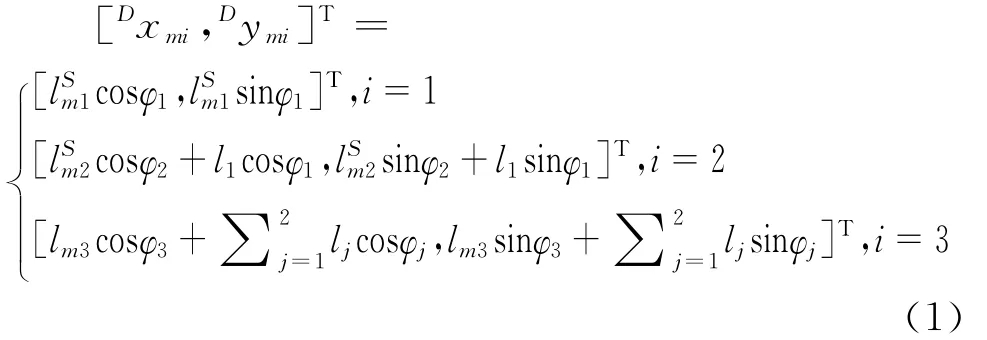
(Dxmi,Dymi)为各连杆质心mi在足端坐标系xDDyD下的坐标;,即第i根连杆的绝对角度。采用拉格朗日方法建立单腿飞行相动力学方程,有:
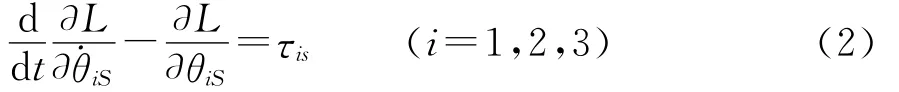
T为系统的总动能;U为系统相对于参考点的总势能。设Δx为弹簧的压缩长度,L=T-U,且
将式(1)和式(3)代入式(2)可得着地相单腿动力学方程为:
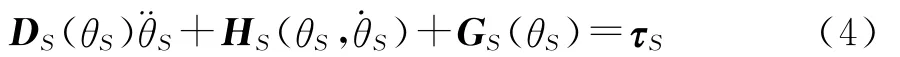
1.2 飞行相运动学和动力学
在如图1b所示的飞行相中,选择髋关节旋转中心B(x0,y0)作为参考点,建立单腿局部坐标系xBByB描述单腿的姿态。B点相对于地面的坐标可通过里程计的航迹推算来获得。髋关节θ1F和膝关节角度θ2F分别描述了大腿和小腿的姿态。
飞行相与着地相相比,多了髋关节中心B在竖直平面内的运动。选取θF=[x0,y0,θ1F,θ2F]T作为广义坐标,此处广义坐标彼此间不完全独立。同样根据D-H法,单腿各部分质心位置在飞行相全局坐标系下分别为:
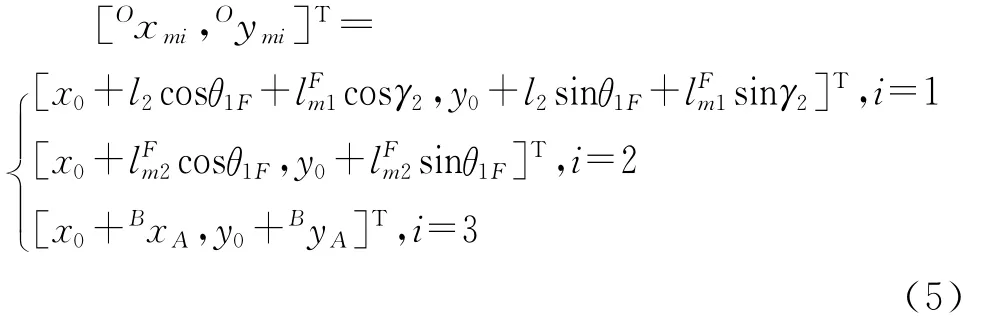
BxA和ByA为A点在坐标系xBByB下的坐标;。
根据拉格朗日法建立类似于式(2)的动力学方程。飞行相动力学与着地相动力学所不同的是,飞行相动能和势能中包含了广义变量x0,y0和其一阶导数,,由于弹簧在飞行相中处于自然未压缩状态,势能中无弹簧弹性势能项。同样的,可以得到飞行相的动力学方程为:
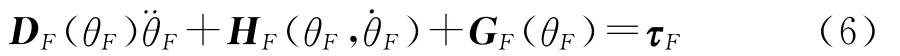
2 单腿竖直跳跃实现策略
上升起跳阶段髋部质心在着地相坐标系中需要满足约束条件,即
a.初始时位置为h0,离地时刻T1的位置达到期望值为h1。
b.离地时刻T1的速度达到期望值为v1。
通过规划起跳姿态和运动速度可以实现跳跃任务。根据上述约束条件,可设定上升起跳质心竖直方向的表达式为:
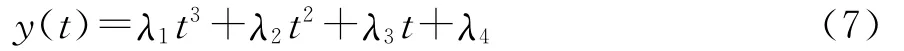
上述约束方程的数学表达式为:
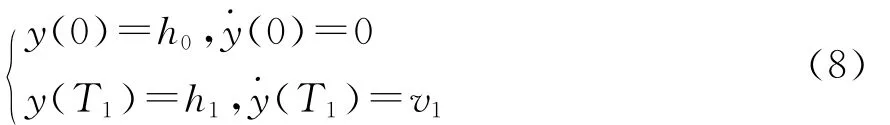
由约束条件解得λi(i=1,2,3,4),于是得:
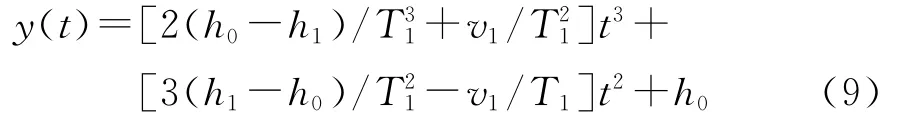
下降压缩过程冲击力过大会对传感器和机械结构造成一定影响,需要通过落地运动规划来尽量减少冲击力。在此采用“软着陆”思路,合理规划运动轨迹,使腿部具有一定弹簧刚度,控制地面冲击力在一定范围内。单腿“软着陆”下降落地过程中,髋部质心在着地相坐标系中需满足约束条件,即
a.下降落地阶段位置由h1变为h0。
b.下降落地结束时,速度由-v1变为0,于是得到约束方程为:
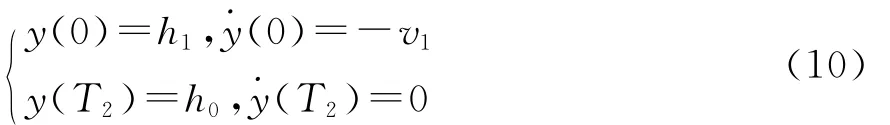
由约束条件解得λi(i=1,2,3,4),得到下降压缩阶段髋部质心竖直位移表达式为:

3 单腿竖直跳跃仿真分析
针对上述模型,采用 MSC.ADAMS和Simulink进行了联合仿真。仿真参数如表1所示。

表1 联合仿真参数设置
根据单腿结构参数情况,选取参数h0=520 mm,h1=620 mm,T1=T2=0.3 s,v1=1.0 m/s,并按照式(9)和式(11),得到上升起跳和下降落地过程髋部质心的竖直位移曲线,如图2所示。
单腿竖直跳跃过程中,足端受力和关节力矩曲线如图3和图4所示。由图3和图4可知,冲击力和关节力矩峰值分别达到了440 N和72 N·m,且跳跃过程中,膝关节力矩显著大于髋关节力矩。在上升起跳阶段,两关节输出力矩迅速增大,使腿部整体获得足够的动能,实现单腿的竖直跳跃。在下降落地阶段,两关节输出力矩迅速减少,使得单腿整体的动能在与地面冲击的过程中消耗。
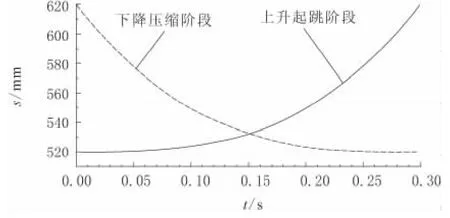
图2 上升和下降阶段髋部质心的竖直位移
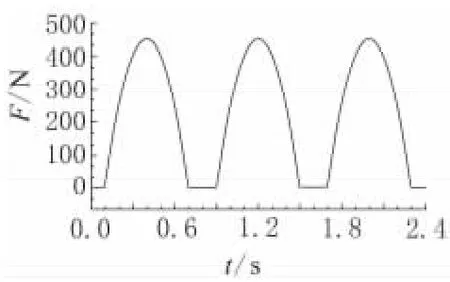
图3 单腿竖直跳跃地面反作用力
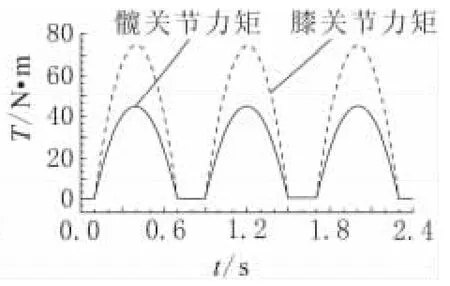
图4 单腿竖直跳跃关节力矩
4 连续竖直跳跃实验
4.1 跳跃实验系统搭建
基于仿生研究设计并制作出的机器人单腿实物样机如图5所示。髋部、大腿和小腿连接部分为转动副。选择液压作为关节驱动方式,两关节由液压缸驱动,各关节均安装角度传感器,机器人关节角度的控制可转化为液压缸位置的控制。小腿部分装有弹簧用于吸收足端与地面接触的冲击并兼具储能功能。小腿上安装直线位移传感器,小腿末端安装脚力传感器。机器人腿部具体结构参数如表2所示。

图5 机器人单腿实物
在实验中,控制器采用美国NI公司的Lab-VIEW构建。关节角度采用角度传感器测量,弹簧变化量用磁致伸缩(LVDT)直线传感器测量,腿末端与地面作用力通过脚力传感器测量。控制器将竖直跳跃算法计算后,通过液压缸的动作命令发给液压系统中比例方向阀,进而控制液压缸运动。液压系统采用比例控制,控制周期为1 ms。

表2 四足机器人单腿参数
4.2 控制方法
要实现单腿竖直连续跳跃,就需要不停地在上升起跳、腾空和下降压缩的状态中切换。下降落地状态需要通过是否触地的判据进行切换。通过直线位移传感器检测小腿的弹簧在下落过程中的形变量,以压缩量判别腿部末端是否着地。
单腿竖直连续跳跃实质上为轨迹跟踪,采用最常用数字PID算法进行控制。具体的控制如图6所示。规划的运动轨迹经运动学反解得到关节角度,进而换算成液压缸长度,液压缸期望长度ld与实际长度lr的偏差e输入增量式PID控制器,PID输出电压u使驱动单元动作,使得实际的运行轨迹跟踪期望轨迹。
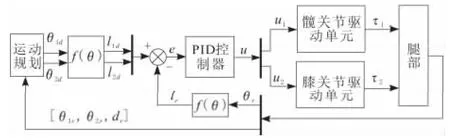
图6 单腿连续跳跃控制
4.3 实验结果
单腿竖直跳跃过程中与地面冲击使得关节角度信号有一定的噪声,实验中对采集的角度信号进行低通滤波处理。实际的跳跃高度可保持在80 mm左右。
单腿竖直跳跃过程中,各关节角度的期望值和实际值如图7所示。由图7可知,实际的跟踪曲线与期望值曲线形状基本一致,由于受液压系统的性能影响,角度跟踪存在一定的相位延迟,液压缸在换向时跟踪误差会稍微偏大,但对整个连续竖直跳跃的实现及稳定性影响不大。
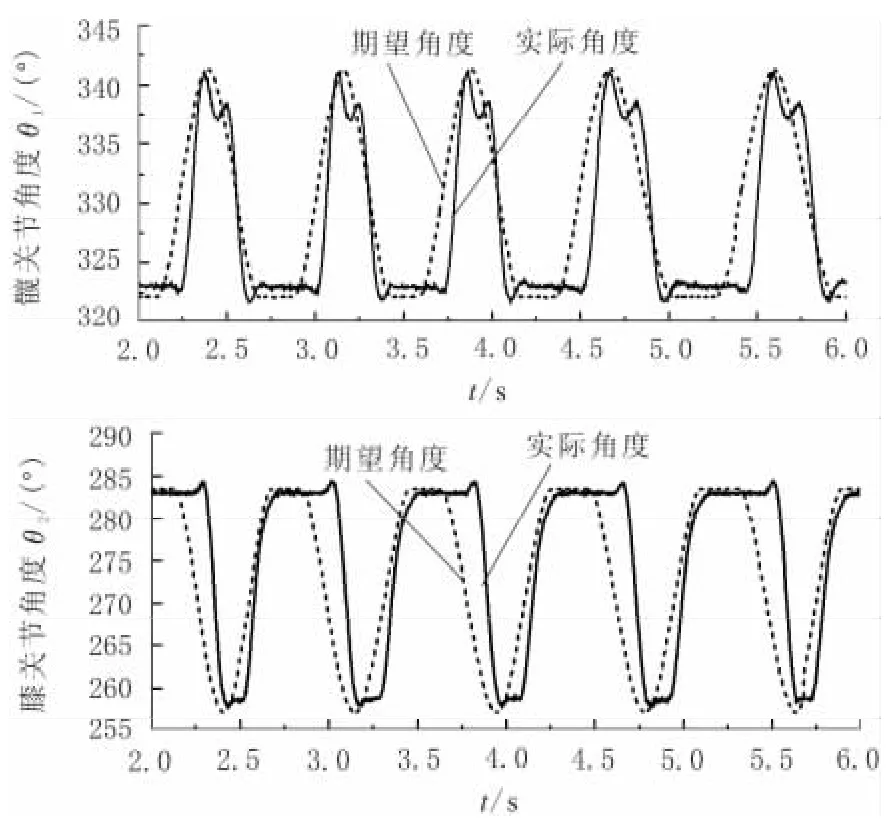
图7 竖直跳跃关节角度跟踪对比
单腿竖直跳跃过程中,腿部末端与地面的接触力曲线如图8所示。由图8可知,力曲线周期与关节角度变化周期一致,有较好的重复性,且最大的冲击力为475 N。
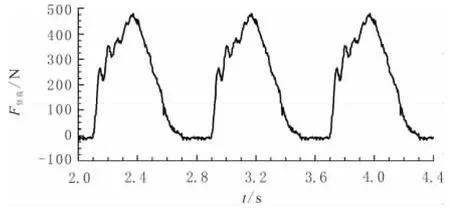
图8 腿部末端与地面接触力曲线
5 结束语
在借鉴仿生学设计机器人单腿结构的基础上,考虑单腿竖直跳跃变约束特点,分别建立了单腿着地相和飞行相的运动学和动力学模型,并进行了仿真分析和跳跃实验。实验结果表明,腿部末端安装弹簧与轨迹规划方法结合能够较好地实现单腿连续竖直跳跃,而且腿部末端与地面冲击力不大,验证了跳跃方法的有效性。
后续将针对机器人单腿竖直跳跃策略及优化目标进行更深入的研究。一方面,从跳跃过程与地面冲击力的角度出发,增加阻抗控制方法,实现腿部变刚度柔顺控制,进一步减少着地过程中的冲击,使跳跃过程更接近于自然界动物的运动模式。另一方面,从能量利用效率的角度出发,研究机器人单腿能量最优跳跃方式,为实现机器人更强的续航能力奠定基础。
[1] Brown B,Zeglin G.The bow leg hopping robot[C].Proceedings of the IEEE International Conference on Robotics and Automation,1998.781-786.
[2] Schmiedeler J P.The mechanics of and robotic design for quadrupedal galloping[D].USA:The Ohio State University,2001.
[3] Hyon S H,Kamijo S,Mita T.“Kenken”——A biologically inspired one-legged running robot[J].Journal of Robotics Society of Japan,2002,20(4):103-112.
[4] 王 猛.仿青蛙跳跃机器人的研制[D].哈尔滨:哈尔滨工业大学,2009.
[5] 葛文杰.仿袋鼠跳跃机器人研究[D].西安:西北工业大学,2007.
[6] Raibert M,Blankespoor K,Nelson G,et al.Bigdog,the rough-terrain quadruped robot[C].Proceedings of the 17th World Congress,2008.10822-10825.
[7] Semini C.Hy Q-design and development of a hydraulically actuated quadruped robot[D].Italy:University of Genoa,2010.
[8] Singh S P,Waldron K J.Attitude estimation for dynamic legged locomotion using range and inertial sensors[C].Proceedings of the 2005 IEEE International Conference on Robotics and Automation,2005.1663-1668.
[9] Raibert M H.Legged robots that balance[M].MA:MIT Press Cambridge,1986.

