湿堆尾矿双向排水大变形固结计算模型

欧孝夺,廖有芳,苏 建,潘 鑫,李结全

(1.广西大学土木建筑工程学院,广西南宁 530004;2.广西大学工程防灾与结构安全教育部重点实验室,广西南宁 530004)

湿堆尾矿双向排水大变形固结计算模型

欧孝夺1,2,廖有芳1,2,苏 建1,2,潘 鑫1,2,李结全1,2

(1.广西大学土木建筑工程学院,广西南宁 530004;2.广西大学工程防灾与结构安全教育部重点实验室,广西南宁 530004)

根据上游法湿堆尾矿的工艺特点,在分析上游法湿堆尾矿渗流固结特性和存在问题的基础上,结合一种适合于上游法尾矿库的排水固结装置的排水特点,在考虑竖向和径向双向排水、变渗透系数及变荷载条件下,采用大变形固结理论推导了尾矿固结计算模型,进而得到以超静孔隙水压力表示的考虑双向排水作用的大变形固结控制方程,并将该方程与Barron固结方程进行比较,验证了计算模型的正确性。采用有限差分法对该大变形固结控制方程进行求解,得到了固结控制方程的差分方程,并利用追赶法等数学方法对差分方程进行了求解。以中铝广西分公司某尾矿库为计算实例,采用该排水固结装置的大变形固结计算模型及数值计算程序进行计算,结果表明该计算模型能有效反映尾矿的固结规律,采用排水固结装置尾矿固结时间缩短了60%以上。

上游法尾矿库;湿堆尾矿;固结装置;大变形固结;径向排水;竖向排水;变荷载;变渗透系数

截至2011年底,我国已建和在建尾矿库达到11946座,其中90%以上的尾矿库采用上游法筑坝[1]。此类上游法尾矿库存在坝体稳定性差和尾矿浸润线高、垂向渗透性差、排水固结缓慢等缺点,容易出现安全隐患[2-5]。为了提高尾矿库安全稳定性,许多学者从絮凝剂、排水工艺、固结措施等方面开展了加快尾矿排水固结的相关研究,并取得了一定的研究成果[6-10]。尾矿的排水固结属于大变形固结范畴,而目前国内外鲜见涉及尾矿大变形固结的研究成果。本文基于大变形固结理论开展上游法湿堆尾矿固结计算模型研究,以期为上游法湿堆尾矿固结计算提供借鉴。

1 上游法湿堆尾矿渗流固结特性

由于泵送吹填入库的需要,初期排入尾矿库中的矿泥含水量极高、流动性强、孔隙比大、渗透系数高、变形能力强,具有大变形固结性质。

根据上游法湿堆尾矿的堆填工艺,尾矿颗粒大小在水平向(径向)及竖向上均呈不均匀分布,而尾矿粒径分布直接影响其渗透系数,从而导致渗透系数在径向及竖向呈现交错分布的情况[11]。细粒层渗透系数可能比粗粒层渗透系数小1或2个数量级,因此细粒薄层的存在对竖向上的渗流影响很大,不可忽略。

由于尾矿泥为分层堆填,对于下层尾矿泥而言,其上覆荷载呈周期性分级增加。在新一层尾矿泥排入库前,尾矿库任意深度处矿泥在自重及上覆荷载作用下已达到了一定的固结度,但孔隙水压力未完全消散,土体未完全固结。当新层尾矿吹填入库后,即在表层增加了新的荷载,库中矿泥在新荷载作用下会重新发生固结作用。

在停止排放矿泥的时间里,尾矿泥浆在库内流动过程中在竖向上粗颗粒首先发生下沉,悬浮于表面的都是颗粒十分细小的悬浮质颗粒,待表面水分蒸发完全后便在表面留下厚度极薄的细粒层,即在矿泥表面会出现一层厚度2～3 mm的泥皮,其渗透系数极小,这就大大地降低了尾矿泥在竖向上的渗透性,也使得尾矿泥的渗流特性更加复杂。

综上所述,上游法湿堆尾矿固结具有变渗透系数、变荷载、大变形等特性。

2 上游法湿堆尾矿排水装置设计

基于上游法湿堆尾矿堆填工艺及排水特点,黄绍铿等[12]设计了一种适用于上游法湿堆尾矿的排水装置,如图1所示。该装置主要由上部悬浮装置和竖向排水带两部分组成,其中竖向排水带可卷曲于悬浮装置中。尾矿泥中的孔隙水经水平(径向)流向排水带,而后由排水带将水排入底部排渗系统,使得尾矿库中矿泥在原有竖向排水的基础上,增加了径向的排水路径,从而加快矿泥排水、缩短固结时间。由于初期矿泥含水量极高,上部悬浮结构所用为轻质材料,故在浮力作用下可实现悬浮结构随尾矿堆积的同步升高。

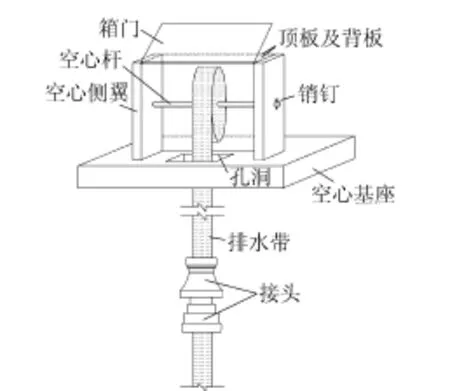
图1 排水装置示意图

在尾矿库平面布置若干个该排水装置(图2),可大大缩短尾矿泥的水平排水渗径而加快尾矿泥的排水进程,在很大程度上降低尾矿库的浸润线,提高尾矿坝的稳定性。本文结合该装置的特点,开展大变形固结计算分析,为该装置的推广应用提供理论参考。

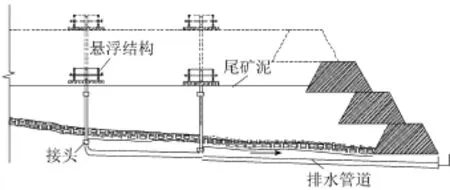
图2 排水装置现场布设剖面示意图

3 计算模型的建立

3.1 数学模型简化

a.尾矿泥的堆填具有成层性,当堆填至第n层时,堆填尾矿泥的总厚度为H,各层的矿泥厚度依次记为h1,h2,…,hi,…,hn,如图3所示(图中Ki(i=1, 2,…,n)为各层矿泥侧压力系数;zi(i=0,1,…,n)为纵向轴线分层标号),尾矿泥初期坝为透水坝,底部具有排水特性;堆场顶面处忽略蒸发等微弱影响因素,为不排水边界条件。

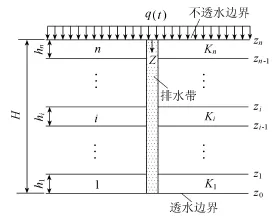
图3 尾矿库成层堆填示意图

b.根据尾矿泥的堆填排放工艺,作用在某层矿泥上的上覆荷载是分级加载的变化荷载,故外荷载按线性变化考虑,其与时间的关系曲线如图4所示。外荷载直至尾矿库满库停排才停止增加,上覆荷载与时间的关系[13]可表示为

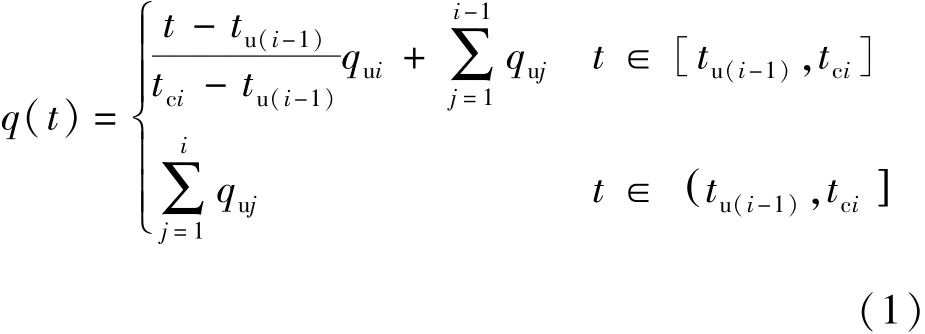
式中:qui为第i级最终荷载值;tci,tui分别为第i级荷载增加结束时间和稳定荷载结束时间;t为总时间。

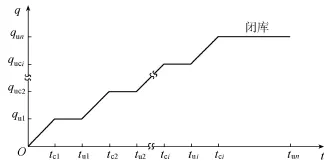
图4 外加荷载与时间关系曲线

c.排水装置在尾矿库堆场平面按梅花形布置,每个竖向排水井的影响范围为六边形(图5),可用一个当量直径为dp的等效面积的圆来代替该六边形区域[14]。其渗流为辐射流,平面上由于水流对称,可将圆周面视为不排水面进行处理,即无水流穿过圆周面[15]。在尾矿库堆场分离出一个计算单元进行分析,该单元外边界考虑为不排水边界,分析时同时考虑径向和竖向的排水固结,半径为rd,排水井半径为rD。

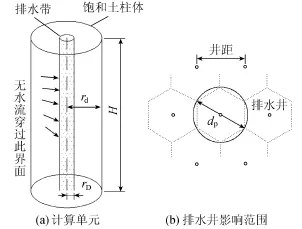
图5 大变形固结模型

3.2 基本假定及坐标系选择

a.土质均质和完全饱和,仅考虑主固结效应,不考虑次固结和蠕变效应。

b.土颗粒及孔隙水为不可压缩物质,固结中所引发的土体压缩变形完全是由土体中的孔隙水外排引起的。

c.径向及竖向均可发生排水固结,水的渗流服从达西渗流定律。

d.土的压缩变形仅在竖向发生,而在径向上不发生压缩。

e.在同一深度处土层径向和竖向的渗透系数相等;竖向不同深度处渗透系数不同。

f.固结过程中将忽略井阻和涂抹效应,假定竖向排水带的排水能力非常强,水平渗流一经流至竖向排水带,渗流水立即被排出。

根据上述假定,径向上仅发生渗流水的运动,因此径向可采用欧拉坐标系。排水井的影响范围考虑为圆柱体,那么在平面上可用极坐标系(ρ,θ),如图6所示。

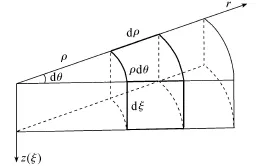
图6 土体固结坐标系及土体微分单元

在竖向上,由于土颗粒相对水流发生竖向的移动,上边界及侧边排水边界均发生了改变,因此竖向可选择流动坐标系,如图6所示,ξ为流动坐标系坐标。

3.3 固结方程推导

3.3.1 应力平衡方程

假定土体微分单元体外加荷载沿深度方向传递为定值,则土体径向应力σρ与竖向应力σξ有σρ= K0σξ[16]的关系,其中K0为土体侧压力系数,那么竖向和径向应力平衡微分方程可分别表示为

式中:ρs为土颗粒的密度;ρw为水的密度;g为重力加速度;e为孔隙比。

3.3.2 液相连续性方程

设土颗粒流动速度为vs,水流速度为vw(vw1为竖向孔隙水流速,vw2为径向的孔隙水流速),则微分单元体渗流情况如图7所示。

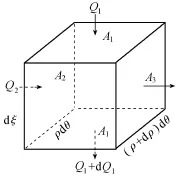
图7 微分单元体渗流示意图

竖向和径向流量的增量分别为

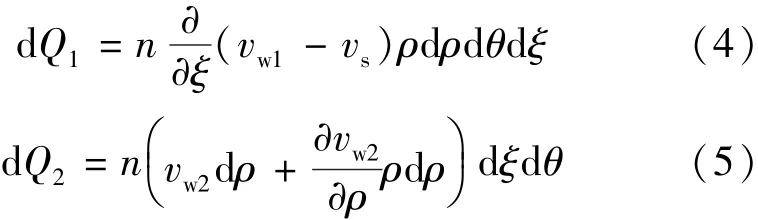
考虑尾矿泥浆颗粒具有不可压缩性,微分单元体积的减小就是孔隙体积变化所致,即

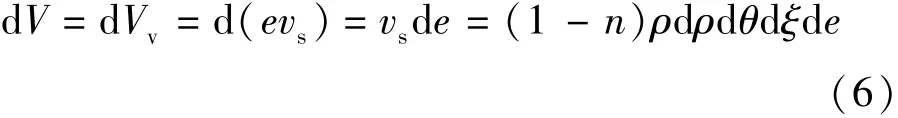
式中dVv为土中孔隙体积变化速率。综合式(4) (5)(6),得到液相连续性方程:

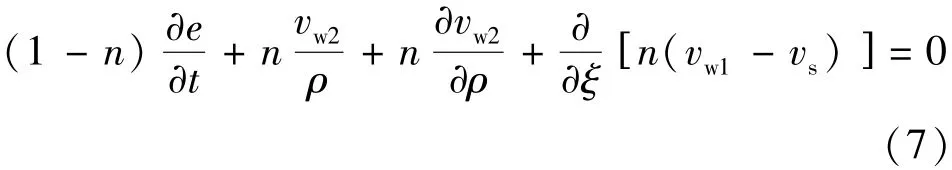
3.3.3 达西渗流方程

在竖向上,考虑土体变形为大变形,孔隙水相对于土颗粒运动,故在采用达西定律时,速度采用相对速度vw1-vs,达西渗流方程可表示为

式中:k为渗透系数;iz为z方向上的水力梯度。在径向上,由于只发生孔隙水渗流,而土颗粒不发生移动,因此可采用径向孔隙水的绝对速度vw2,达西渗流方程表达式如下:

式中iρ为ρ方向上的水力梯度。

通过任意时刻z和ρ方向孔隙水压力ue反解得到iz和iρ,代入式(8)(9)得到达西渗透方程:

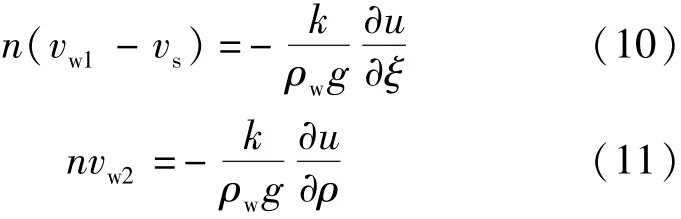
式中u为超静孔隙水压力。

3.3.4 有效应力方程

根据有效应力原理,在任一时刻饱和土体上作用的总应力σ均由孔隙水压力ue及作用在土骨架上的有效应力σ′共同承担,总应力表达式为

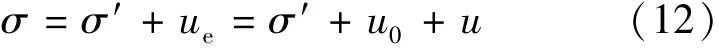
式中u0为流动坐标系下某微分单元体静水压力,其表达式为

则有效应力竖向和径向的微分表达式分别为

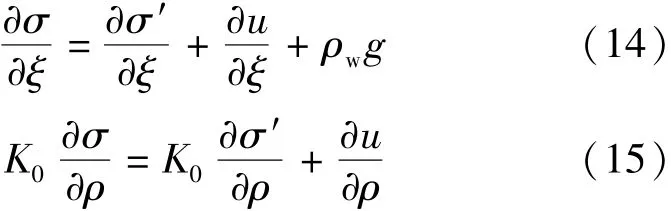
将式(2)代入式(14)、式(3)代入式(15)可得

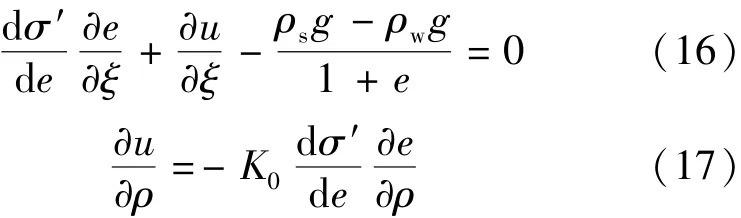
3.3.5 以超静孔压为变量的控制方程

将达西渗透方程代入液相连续性方程可得

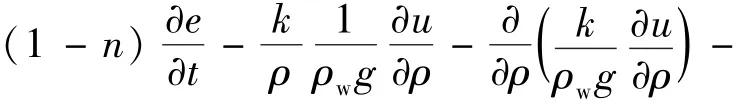
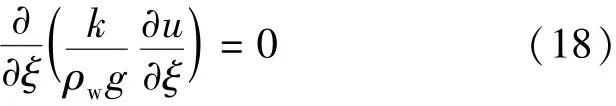
把方程(18)化为以超静孔隙水压力表示的考虑径向和竖向排水作用的大变形固结控制方程:

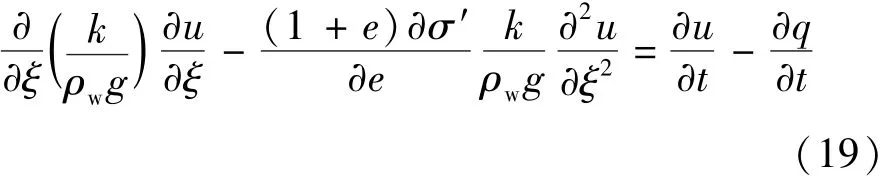
将流动坐标系下的式(19)转换为固相坐标系下的表达式:

即

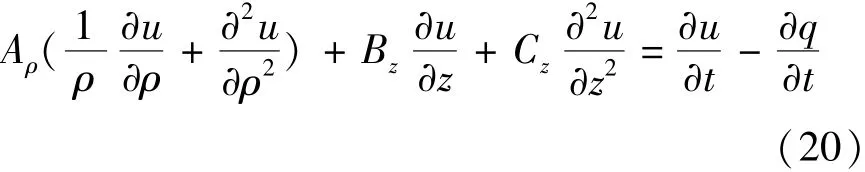
其中

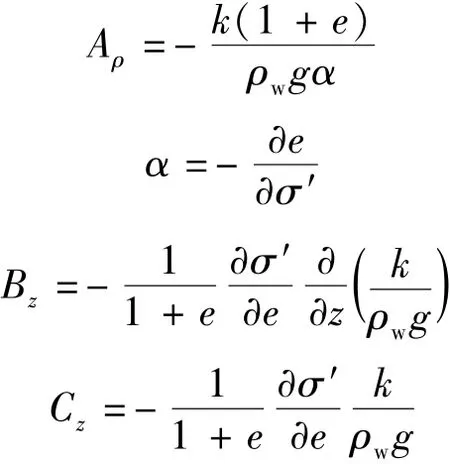
式中:Aρ为径向固结系数:Bz、Cz为竖向大变形系数项。式(20)即为双向排水大变形固结计算模型建立的模型控制方程。

3.4 固结方程比较

Barron固结理论与太沙基一维固结理论的基本假定相同,均是建立在小变形基础上的。如按照这些假定,具体考虑如下:渗透系数k不变,压缩系数且为常数,引入固结系数也为常数;因为所考虑变形为小变形(变形量微小),因此可认为流动坐标与固相坐标微量相同,即dξ=dz;此外,考虑外荷载是一次施加的,那么结合以上分析,式(20)简化后的公式形式如下:

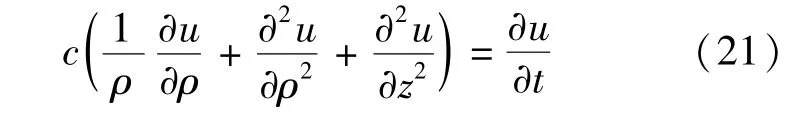
由于竖向与径向渗透系数相同,固结系数也相同,此时式(21)即为Barron固结方程。即本文推导的考虑双向排水的大变形固结控制方程经条件简化后可变为Barron固结方程,进一步验证了计算模型公式(式(20))的正确性。

4 差分法求解控制方程

式(20)所表示的大变形固结控制方程为高阶偏微分方程,一般情况下直接求解方程以获得解析解不太可能,下面采用有限差分法求解。

4.1 边界条件

根据固结计算模型(图5),固结方程式需要满足的一些求解条件如下:

a.初始条件。初始状态下有效应力全部由孔隙水承担,数学表达式为式中:ρ′为浮密度;Gs为土粒相对密度。

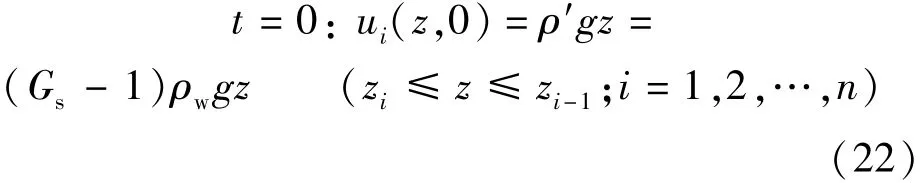
b.上边界条件。由于不考虑大气蒸发、降水等因素,因此上边界为不排水边界,数学表达式为

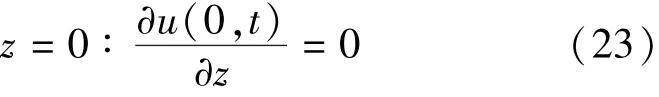
c.下边界条件。由于尾矿初期坝为透水坝,底部排水设施排水能力很大,水流流至此处便被完全排走,因此下边界为排水边界,数学表达式为

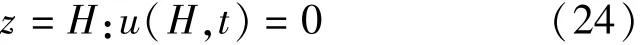
d.内径边界条件。由于竖向排水带的排水能力很大,因此内径边界考虑为排水边界,数学表达式为

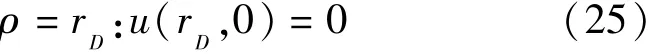
e.外径边界条件。由于排水固结装置在尾矿库平面位置上呈梅花形布置,渗流为辐射流,在平面上水流对称,因此可将圆周面视为不排水边界,数学表达式为

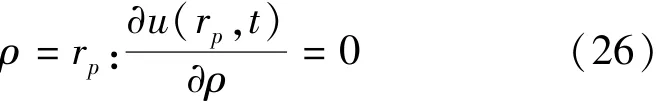
f.层间连续性条件。相邻层的连续性条件主要考虑层间超静孔隙水压力及径向和竖向渗流应符合连续性条件,将其转换为数学表达式如下:

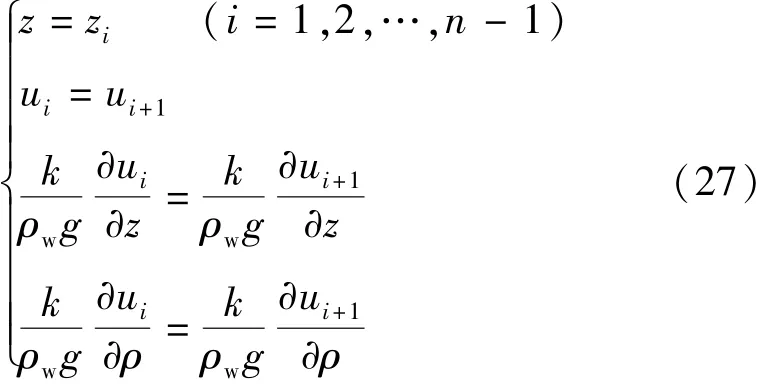
4.2 大变形固结控制方程的有限差分方程求解

高阶偏微分方程的有限差分求解需将求解区域进行空间和时间的离散划分,此外外荷载也需要进行相应的离散。

4.2.1 网格设计划分

如图3所示,将厚度为H的尾矿库分为n层尾矿泥,那么每层尾矿泥的厚度即为H/n,在此基础上,每层再细划分为x个薄层。在径向上划分总网格数量为L,竖向上划分总网格数量为J,网格的划分如图8所示,径向和竖向网格距分别为

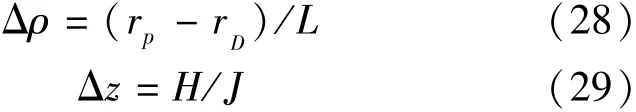
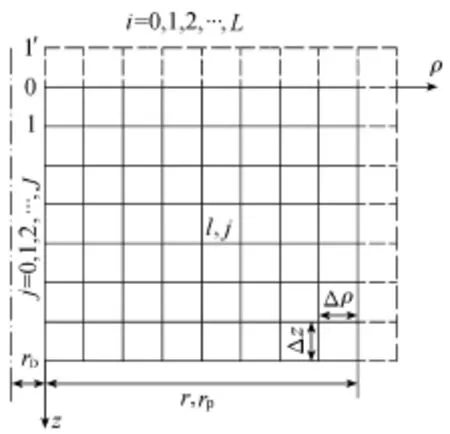
图8 空间网格划分

4.2.2 时间步长处理

对时间t进行离散即得到时间步长Δt,时间t与Δt二者的关系可表示为

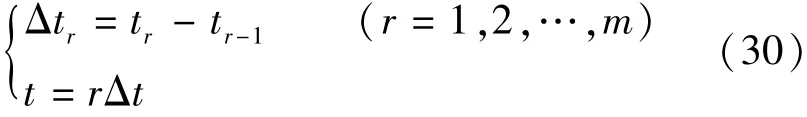
4.2.3 外荷载的离散

在第r时间段内,相应的荷载增量即离散荷载段为

式中q(tr)为时间点tr处的上覆土压力荷载。

4.2.4 差分方程求解

采用交替方向隐式差分法[17]求解,该方法的特点是在tr与tr+Δt之间假设有一个过渡的中间时刻tr+Δt/2,计算分两步进行:

第一步:从tr到tr+Δt/2对径向(ρ方向)采用隐式差分格式求解,在竖向对z采用显式差分格式求解,得到的差分方程如下:

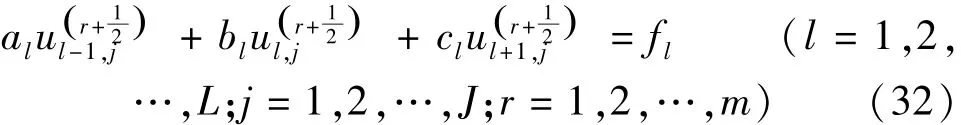
其中

第二步:从tr+Δt/2到tr+Δt对竖向(z向)采用隐式差分格式求解,在径向对ρ采用显式差分格式求解。从第一步计算得到的中间时刻tr+Δt/2的超静孔隙水压力变量可以作为第二步计算的已知值,得到的差分方程如下:

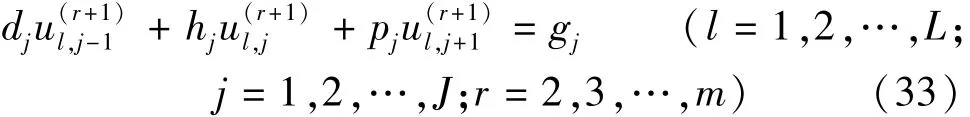
其中

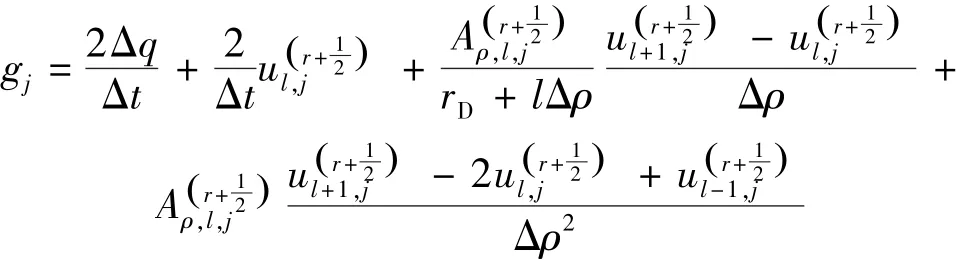
将式(32)和(33)转换为系数矩阵为对角占优的三对角方程组,采用追赶法可快速求解得到tr到中间时刻超静孔隙水压力值;将其作为tr+Δt/2到tr+Δt时段的已知值即可求解时段末超静孔隙水压力的值。至此便完成了一个时间步Δt的计算,依此求解方法交替进行差分方程的求解,即可求解各个时间段的待求参数。

计算得到各时刻下的超静孔隙水压力u后,通过有效应力、孔隙比与有效应力之间的非线性关系式经公式换算得到各个时刻的有效应力σ′及孔隙比e,而后通过计算得到各薄层对应时刻下的应变固结度、应力固结度、沉降量等。

平均应变固结度和平均应力固结度分别为

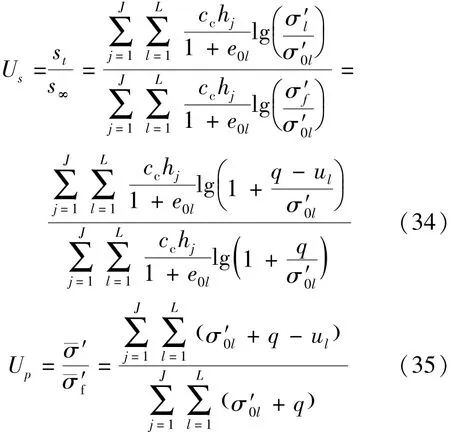
式中:cc为土的压缩指数;hj为各层土压缩量;q为作用在土层上随时间变化的外加荷载;σ′l、σ′0l分别为径向第l个单元格的有效应力和施加外荷载前的有效应力;σ′f为固结完成时单元格的有效应力。

5 工程实例应用计算分析

以位于广西平果县境内的中铝广西分公司某尾矿库为例,吹填入库的平果铝尾矿每层矿泥厚度为0.5 m左右,而后待充填层排水固结由初期含水率70%降至40%左右后再重新充填新的一层,而这段固结过程所需要的时间为40 d左右。

采用图1所示排水固结装置,利用大变形固结计算模型及数值计算程序进行求解计算。计算时土粒相对密度等于3.26,初始渗透系数取值为2.34× 10-3cm/s,初始孔隙比为1.83。以两层矿泥为计算模型,每层土厚0.5 m。通过输入初始条件、边界条件及实验数据拟合得到的渗透系数和孔隙比与有效应力之间的函数关系,求解得到每一土层的超静孔隙水压力分布,进而求解得到每层土层固结度的时空分布情况。选取土层平均固结度达到60%时所需时间作为评定标准,对排水半径rp=1.0 m工况进行计算分析,结果如下:

a.孔隙水压力在竖向上沿着土层中部并不是对称分布的,最大孔隙水压力出现在土层中部以下位置。随着固结作用的进行,最大孔隙水压力作用位置逐步向土层中部转移,当靠近固结末期时,孔隙水压力在竖向上沿土层中部基本上呈对称分布。

b.获得了底层及上部土层在rp=1.0 m条件下的平均应力及应变固结度与时间关系曲线,发现在相同的条件下,任意时刻平均应变固结度都要大于平均应力固结度(Us＞Up),即尾矿泥超静孔隙水压力的消散速度较沉降速度慢。

c.在rp=1.0 m条件下,平均应力固结度达到60%时,上层矿泥需要19 d左右,底层需要的时间为16 d左右;平均应变固结度达到60%时,上层矿泥需要16 d,底层矿泥需要14 d。

通过上述工程实例分析可见,尾矿土强度增长初期呈非对称性;以孔隙水压测算固结度预估土体强度较沉降测算偏保守;排水固结装置能缩短尾矿固结时间60%以上,该大变形固结计算模型能有效反映尾矿固结规律,在尾矿类超软土固结计算中具有很大的实用性。

6 结 语

本文结合一种新型尾矿排水装置,将大变形固结理论引入该装置作用下尾矿固结计算模型,推导得到以超静孔隙水压力为变量,可同时考虑径向和竖向双向排水、变荷载、变渗透系数的大变形固结控制方程,并利用追赶法得到了有限差分方程的求解式,进而得到该大变形固结计算模型的数值计算方法。

工程实例计算结果表明,该排水装置能将尾矿固结时间缩短60%以上,计算模型能有效测算尾矿固结状态及规律,可为该排水固结装置的推广应用及尾矿质超软土的固结计算提供参考。

[1]田文旗,谢旭阳.我国尾矿库现状及安全对策的建议[J].中国矿山工程,2009,38(6):42-43.(TIAN Wenqi, XIE Xuyang.Tailings pond situation in China and safety countermeasuressuggestions[J].ChinaMine Engineering,2009,38(6):42-43.(in Chinese))

[2]于斯滢,邵龙潭,刘士乙.基于有限元极限平衡法的尾矿坝坝体稳定分析[J].岩土力学,2013,34(4):1185-1190.(YU Siying,SHAO Longtan,LIU Shiyi.Stability analysis of tailings dam based on finite element limit equilibrium method[J].Rock and Soil Mechanics,2013, 34(4):1185-1190.(in Chinese))

[3]刘春刚.细砂尾矿坝静力和动力稳定性分析研究[D].北京:北京交通大学,2012.

[4]李强,张力霆,齐清兰,等.基于流固耦合理论某尾矿坝失稳特性及稳定性分析[J].岩土力学,2012,33(增刊2):243-250.(LI Qiang,ZHANG Liting,QI Qinglan,et al.Instability characteristics and stability analysis of a tailings dam based on fluid-solid coupling theory[J].Rock and Soil Mechanics,2012,33(Sup2):243-250.(in Chinese))

[5]张世文,王红艳.影响尾矿坝安全稳定性因素分析及对策[J].矿业工程,2004,2(2):61-62.(ZHANG Shiwen, WANG Hongyan.Analysis of factors influencing stability of tailing dam and measures for improving dam’s stability [J].MiningEngineering,2004,2(2):61-62.(in Chinese))

[6]欧孝夺,曹净,周东,等.广西平果铝尾矿泥浆化学絮凝处理试验研究[J].岩土工程学报,2003,25(2):201-203.(OUXiaoduo,CAOJin,ZHOUdong,etal. Experimental study on chemical flocculating action of waste flush fluid[J].Chinese Journal of Geotechnical Engineering,2003,25(2):201-203.(in Chinese))

[7]尹光志,张千贵,魏作安,等.尾矿细观结构变形演化非线性特征试验研究[J].岩石力学与工程学报,2011,30 (8):1604-1612.(YIN Guangzhi,ZHANG Qiangui,WEI Zuoan,etal.Experimentalstudyofnonlinear characteristics of deformation evolution for meso-scopic structure oftailings[J].ChineseJournalofRock Mechanics and Engineering,2011,30(8):1604-1612.(in Chinese))

[8]李志平,彭振斌,肖尊群,等.含水率影响下尾矿砂内摩擦角随标贯击数变化研究[J].岩土力学,2013,34 (5):1340-1344.(LI Zhiping,PENG Zhenbin,XIAO Zunqun,et al.Variation of internal friction angle of tailings with standard penetration number under influence of water content[J].Rock and Soil Mechanics,2013,34(5): 1340-1344.(in Chinese)).

[9]沈楼燕,王敏杰,王磊.一种新型尾矿坝同步排渗加固装置:中国,CN200920188635.3[P].2009-08-19.

[10]尹光志,张千贵,魏作安,等.孔隙水运移特性及对尾矿细观结构作用机制试验研究[J].岩石力学与工程学报,2012,31(1):71-79.(YIN Guangzhi,ZHANG Qiangui,WEIZuoan,etal.Experimentalstudyof migration characteristics of pore water and its effect on meso-structure of tailings[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(1):71-79.(in Chinese))

[11]颜学军.上游法尾矿堆筑坝体沉积规律探讨[J].稀有金属与硬质合金,2008,36(2):54-58.(YAN Xuejun. Deposited law of the upstrenm tailings pile dam[J].Rare Metals and Cemented Carbides,2008,36(2):54-58.(in Chinese))

[12]黄绍铿,欧孝夺,廖有芳,等.一种可随尾矿库同步自动升高排水固结装置:中国,ZL201120063225.3[P]. 2011-11-16.

[13]常林越,王金昌,朱向荣.多级线性荷载下饱和软黏土一维大应变固结解析解[J].岩土力学,2009,30(8): 2343-2347.(CHANG Linyue,WANG Jinchang,ZHU Xiangrong.An analytical solution of 1-D finite strain consolidation of saturated soft clay under multistep linear loading[J].Rock and Soil Mechanics,2009,30(8): 2343-2347.(in Chinese))

[14]徐至钧,王曙光,全科政,等.建筑地基处理工程手册[M].北京:中国建材工业出版社,2005:74-75.

[15]李广信.高等土力学[M].北京:清华大学出版社, 2005:300-301.

[16]卢廷浩.土力学[M].南京:河海大学出版社,2005:49-50.

[17]PEACEMAN D W,RACHFORD H H.The numerical solution of parabolic and elliptic differential equations [J].SIAM Journal,1955(3):28-41.

Large-strain consolidation calculation model on both horizontal and vertical drainage of wet filling tailings//

OU Xiaoduo1,2,LIAO Youfang1,2,SU Jian1,2,PAN Xin1,2,LI Jiequan1,2
(1.College of Civil Engineering and Architecture, Guangxi University,Nanning 530004,China;2.Ministry of Education Key Laboratory of Disaster Prevention and Structural Safety,Guangxi University,Nanning 530004,China)

According to the wet landfill process of upstream tailings,its seepage consolidation characteristics and existing problems are analyzed and additionally,it is put forward based on a drainage device that is suitable for about upstream tailings.With the establishment of the mathematical model,it was possible to derive the formula that considers vertical and radial drainage,varying permeability coefficient,and variable load condition at the same time.The governing equations of large-strain consolidation with both horizontal and vertical drainage are reduced,which is denoted by excess pore water pressure.By comparing study of that governing equations and Barron consolidation formula,we assessed the accuracy of the proposed model.Using the finite difference method to derive the resulting of large strain consolidation of differential equations,thus obtaining the differential equations of consolidation equations an then solving it by using mathematical methods like Pursuit Method.Using the Guangxi Branch of Chalco aluminum tailings as case study,the results show that this calculation model can effectively reflect the consolidation law of the tailings slurry,and the consolidation time of tailings slurry is shortened by more than 60%.

upstream tailings;wet filling tailings;drainage device;large-strain consolidation;horizontal drainage;vertical drainage;time dependent loading;variable permeability coefficient

TV649;TD-05

:A

:1006-7647(2014)05-0028-07

10.3880/j.issn.1006-7647.2014.05.006

2013-0811 编辑:熊水斌)

国家自然科学基金(51168004)

欧孝夺(1970—),男,广西来宾人,教授,博士,主要从事环境岩土工程及尾矿库安全研究。E-mail:ouxiaoduo@163.com