基于数字岩心研究流体性质对裂缝性低渗透储层弹性参数的影响规律
孙建孟,闫国亮,姜黎明,崔利凯,赵建鹏,崔红珠
(1.中国石油大学地球科学与技术学院,山东青岛266580;2.中国石油勘探开发研究院西北分院,甘肃兰州730020; 3.中国石油集团测井有限公司技术中心,陕西西安710077;4.中国石油集团测井有限公司长庆事业部,陕西西安710077)
基于数字岩心研究流体性质对裂缝性低渗透储层弹性参数的影响规律
孙建孟1,闫国亮2,姜黎明3,崔利凯1,赵建鹏1,崔红珠4
(1.中国石油大学地球科学与技术学院,山东青岛266580;2.中国石油勘探开发研究院西北分院,甘肃兰州730020; 3.中国石油集团测井有限公司技术中心,陕西西安710077;4.中国石油集团测井有限公司长庆事业部,陕西西安710077)
为研究裂缝及流体性质对低渗透储层弹性参数的影响规律,采用X射线CT扫描技术构建低渗透储层岩石的3维数字岩心,应用图像处理算法加入定向排列的平行便士状裂缝,形成横向各向同性数字岩心,采用扩展的有限元方法计算含有裂缝的数字岩心的弹性模量,分析裂缝及流体性质对其弹性模量的影响规律。结果表明:裂缝纵横比和密度保持不变,随流体体积模量的增加,纵波各向异性参数呈线性趋势减小;裂缝密度和流体性质不变,随裂缝纵横比增加,储层岩石的弹性模量均呈线性增加;裂缝纵横比和流体性质不变,随裂缝密度增加,储层岩石的弹性模量也呈线性减小。
测井;裂缝性低渗透储层;岩石性质;弹性模量;数字岩心;有限元方法
由于定向应力的作用,低渗透储层存在的自然裂缝或压裂缝通常表现为具有一定取向且相互平行的裂缝模式,形成裂缝性低渗透储层[1]。裂缝的存在及裂缝中填充流体的性质对裂缝岩石的弹性性质有重要的影响,会表现出大的地震各向异性。定量研究裂缝岩石弹性性质随所含流体变化的特征对于深入了解岩石物理性质,特别是对油气田开发具有重要意义。由于缺少表征岩石全面结构的资料,岩石物理模型主要局限于经验公式[2]、上下边界理论[3]、有效介质理论[4-9],这些都不完全令人满意。随着计算机技术的发展,可以基于微观结构的数字模型来直接求解线性弹性方程,从而得到岩石的弹性参数。Knackstedt[10]利用有限元方法计算了枫丹白露砂岩的体积模量与剪切模量,数值计算结果与Han[2]的实验结果一致。Roberts[11]利用有限元方法计算了随机多孔材料的弹性性质,结果表明在整个孔隙度范围内,多孔材料的杨氏模量与固体相的泊松比无关。Dina[12]等基于数字岩心用有限元的方法研究了部分饱和岩石的弹性性质,并把计算结果与低频Gassmann-Wood方程和高频Gassmann-Hill方程进行了比较,发现岩石均匀饱和情况下计算结果与低频Gassmann-Wood方程计算结果一致。但是,上述研究都没有进行裂缝岩石弹性性质随所含流体变化特征的研究。笔者基于重建的裂缝性低渗透储层数字岩心,采用有限元方法计算不同裂缝参数和流体性质下弹性模量的变化规律并与没有裂缝发育的岩石进行对比,分析裂缝开度、长度及流体性质对裂缝性低渗透储层弹性参数的影响规律。
1 裂缝性低渗透储层岩石数字岩心建模
裂缝性低渗透储层岩石一般具有各向异性特征,各向异性的存在使岩石的弹性性质研究变得尤为复杂。一般情况下,岩石的各向异性特征可以用相对简单的横向各向同性来模拟。为了研究横向各向同性岩石的弹性性质,构建了具有横向各向同性的裂缝性低渗透储层岩石的数字岩心。建模步骤分为两步:首先获取具有各向同性特征的低渗透储层岩石基质的3维数字岩心;然后在岩石基质中加入一系列定向排列的裂缝,得到具有横向各向同性特征的裂缝性数字岩心。
目前,建立岩石基质3维数字岩心的方法主要有两大类:一类是数学方法,通过岩石2维薄片图像获得的统计信息来重建数字岩心,包括随机法和过程模拟法两种;另一类是物理方法,通过实验仪器扫描直接构建数字岩心,包括切片组合扫描法和X-CT扫描法两种。与数学方法相比,物理方法构建的3维数字岩心具有直观、准确的优点。
切片组合扫描法通过逐层刨光和切割岩心并进行高精度成像得到,不仅会破坏岩心的完整性,而且非常耗时。X-CT扫描法可以无损地检测非透明物体的组成及结构[13-14],因此采用该方法构建低渗透储层岩石的数字岩心。X射线CT扫描系统得到的最原始的图像是反映岩心径向X射线吸收系数的一系列投影图像,应用滤波(卷积)反投影技术处理后得到岩心的3维灰度图像。
图1(a)为某低渗透储层砂岩岩心(岩心编号为CJ157,实验测量孔隙度为9.2%)扫描得到的3维灰度图像的一个切片,扫描分辨率为2μm/像素。图像中像素点灰度值反映了岩石各组分密度,像素点越亮,即灰度值越大,表示密度越大。从图中可以直接识别出孔隙的位置(图像上比较暗的像素点),但孔隙与骨架的边缘比较模糊,需要对图像进行滤波处理,从而提高孔隙和骨架的对比度[15]。图1 (b)为采用中值滤波算法对图1(a)滤波处理后的结果。最后选取合适的阈值将灰度图像分割为二值图像,分割结果见图1(c)。将二值化后的图像逐层叠合,得到CJ157岩心的3维数字岩心,如图1(d)所示。图中红色部分为孔隙,蓝色部分为骨架,孔隙度为8.8%,与CJ157岩心实验测量的孔隙度9.2%接近。

图1 CJ157砂岩的数字岩心Fig.1 Digital core of CJ157
通过数字图像处理技术把一系列定向排列的便士形状裂缝嵌入岩石基质中,从而得到横向各向同性的数字岩心,如图2所示。图中便士形状裂缝的3个半轴满足a2=a3≫a1。图3为施加裂缝后CJ157砂岩数字岩心的横截面。裂缝密度和纵横比是定量描述裂缝的两个重要参数。其中纵横比a定义为:α=a1/a2;裂缝密度e计算公式为

式中,N为裂缝总的数目;V为数字岩心的体积;φc为裂缝孔隙度。在数值模拟中设定便士形状裂缝厚度为3个像素点,直径为24个像素点,则纵横比为0.125。

图2 施加裂缝后CJ157砂岩的数字岩心Fig.2 Digital core of sandstone CJ157 with cracks

图3 施加裂缝后CJ157砂岩数字岩心的水平横截面Fig.3 Horizontal cross-section of digital core of sandstone CJ157 with cracks
2 理论和数值模拟方法
2.1 各向异性Gassmann理论
各向同性Gassmann流体替换理论适用于各向同性岩石而不适用于各向异性岩石流体替换的研究,因此不能用于裂缝中饱和流体岩石弹性性质的研究。Gassmann[16]随后给出了适用于各向异性介质的流体替换理论,称为各向异性Gassmann理论。该理论假定在岩石孔隙空间中流体压力是均衡的,所以只适用于低频条件下各向异性岩石弹性性质的研究。
干岩石的弹性模量和流体饱和岩石弹性模量的关系满足:
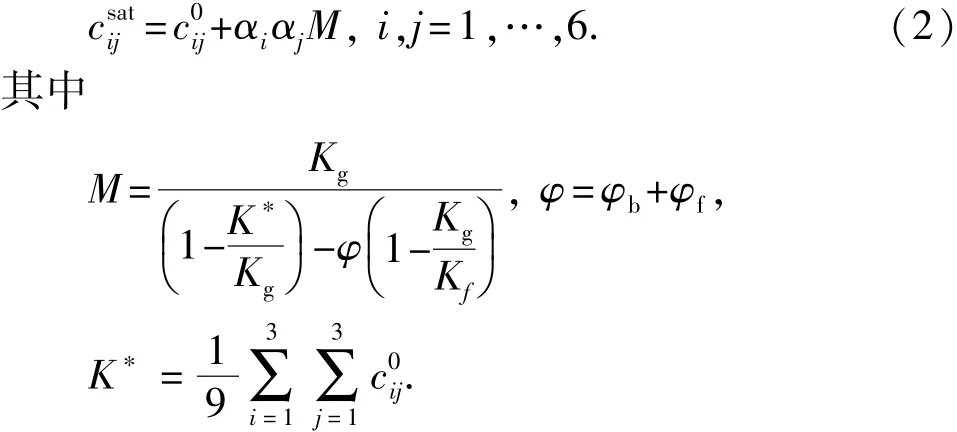
对于横向各向同性岩石,其弹性刚度矩阵中含有5个独立的弹性参数。式(2)中比例系数αi、αj可以表示为
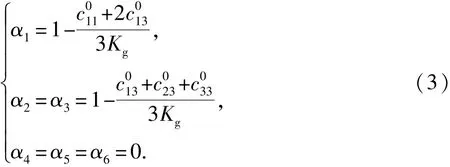
Thomsen各向异性参数ε、γ、δ可以用来描述横向各向同性介质的各向异性程度[17],具体定义为
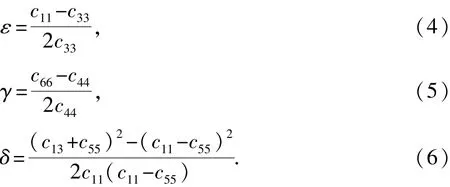
式中,ε为度量准纵波各向异性的参数,ε越大,介质的纵波各向异性越大,ε=0时,纵波无各向异性; γ可以看作是度量准横波各向异性强度,或横波分裂强度的参数;δ主要控制水平垂直正交方向上的各向异性强弱。
2.2 有限元方法
由于数字岩心是由离散的体素组成,每一个体素可以视为一个立方体单元,因此应用有限元方法计算岩石物理属性时无需进行网格划分。在3维数字岩心的基础上,利用有限元法计算岩石弹性模量的理论基础是变分原理。对于给定的数字岩心,沿主应力和切应力方向分别施加一个宏观应变,通过使系统的弹性自由能En最小来确定每个像素点上的最终弹性位移分布。根据变分原理,求解每个像素点上的位移分布问题转化为求解系统线性弹性自由能极值的问题,并最终确定数字岩心的有效弹性模量。为使能量En取极小值,需满足能量对变量um(结点弹性位移)的偏导数均为零,即

在数值求解过程中,当能量En对第m个结点弹性位移的偏导数构成的梯度矢量的平方和小于某一给定允许误差时,可近似认为等式(7)成立,即确定了3维数字岩心中的应力分布和有效弹性参数。
对于横向各向同性岩石,具有5个独立参数,执行一次数值模拟难以求取所有的弹性参数,因此可以利用弹性方程σ=Cε的线性关系,引入6个正交应变基矢,其中α表示基矢的数目,i(i=1,…,6)表示Voigt指数,应用这6个正交基矢足以求出刚度矩阵的36个元素。图4为6个应变基矢的示意图,其中(a)~(c)为轴向应变,(d)~(f)为切向应变,具体表达式为ε1=(1,0,0,0,0,0),ε2=(0,1,0,0, 0,0),ε3=(0,0,1,0,0,0),ε4=(0,0,0,1,0,0),ε5= (0,0,0,0,1,0),ε6=(0,0,0,0,0,1)。通过选其中一个应变基矢作为宏观应变条件执行模拟,可以得到6个宏观应力。根据弹性方程的线性关系,这6个宏观应力定义了刚度矩阵Cαβ的一列,因此分别独立执行6次模拟便可以得到刚度矩阵的所有元素。由于横向各向同性岩石含有5个独立参数,所以仅需执行两次模拟,就可以得到所求参数。扩展的数值模拟算法不仅能计算各向同性岩石的弹性参数,也能计算具有横向各向同性岩石的弹性参数。
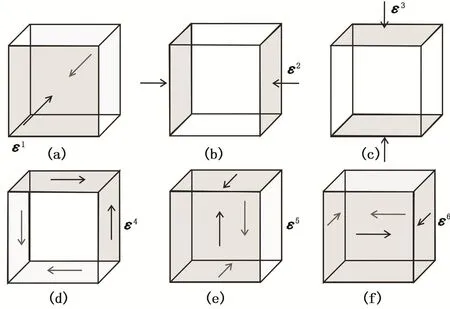
图4 6个宏观应变基矢Fig.4 Six basis vectors of macro-strain
3 裂缝性低渗透储层弹性性质的影响因素
3.1 数值算法的验证
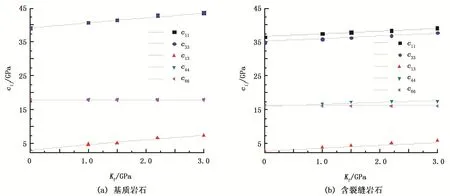
图5 刚度矩阵元素与流体模量的关系Fig.5 Relationship between stiffness matrix and fluid modulus
基质岩石的刚度矩阵与流体模量的关系如图5 (a)所示。从图中可以看出,所选的基质岩石是各向同性的,c11与c33相等,并随流体模量的增加而增加; c44与c66相等,即岩石的剪切模量μ,这两个量与流体性质无关,这与各向同性Gassmann理论也是相符的。通过对比数值模拟结果(图中散点)与利用各向同性流体替换Gassmann理论计算的结果(图中实线),发现数值模拟结果和理论计算结果吻合非常好,证实了数值算法的正确性。
3.2 流体性质对储层弹性性质的影响
基于构建的裂缝性低渗透储层横向各向同性数字岩心,利用有限元方法计算了岩石的弹性参数并与各向异性Gassmann理论计算结果进行了比较,如图5 (b)所示。图中给出了含裂缝岩石的刚度矩阵与流体模量的关系,其中裂缝密度为0.05。从图上可以看出嵌入基质岩石的平行裂缝引起了显著的各向异性。刚度矩阵元素c11和c33发生偏离,并且在平行于对称轴方向(即c33方向)岩石变得更软。c44与c66随流体模量的增大产生了很小的偏差,这说明流体对切向弹性参数影响比较小。通过对比数值模拟结果(图中散点)与利用各向异性流体替换Gassmann理论计算的结果(图中实线),发现数值模拟结果和理论计算结果基本吻合,说明所扩展的数值模拟算法用于气层岩石各向异性研究是可行性的。基于扩展的数值模拟算法进一步研究了各向异性参数随流体模量的变化关系,如图6所示。从图中可以看出,当流体模量为0时,即干岩石,纵波各向异性参数ε最大,随流体体积模量的增加而减小。
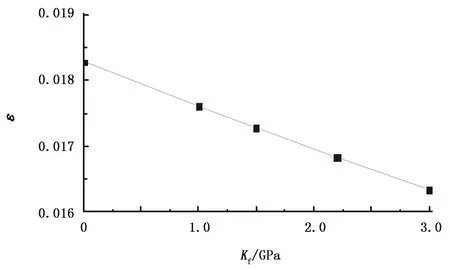
图6 纵波各向异性参数ε与流体体积模量的关系Fig.6 Relationship between anisotropy parameter ε of longitudinal wave and fluid bulk modulus
3.3 裂缝对储层弹性性质的影响
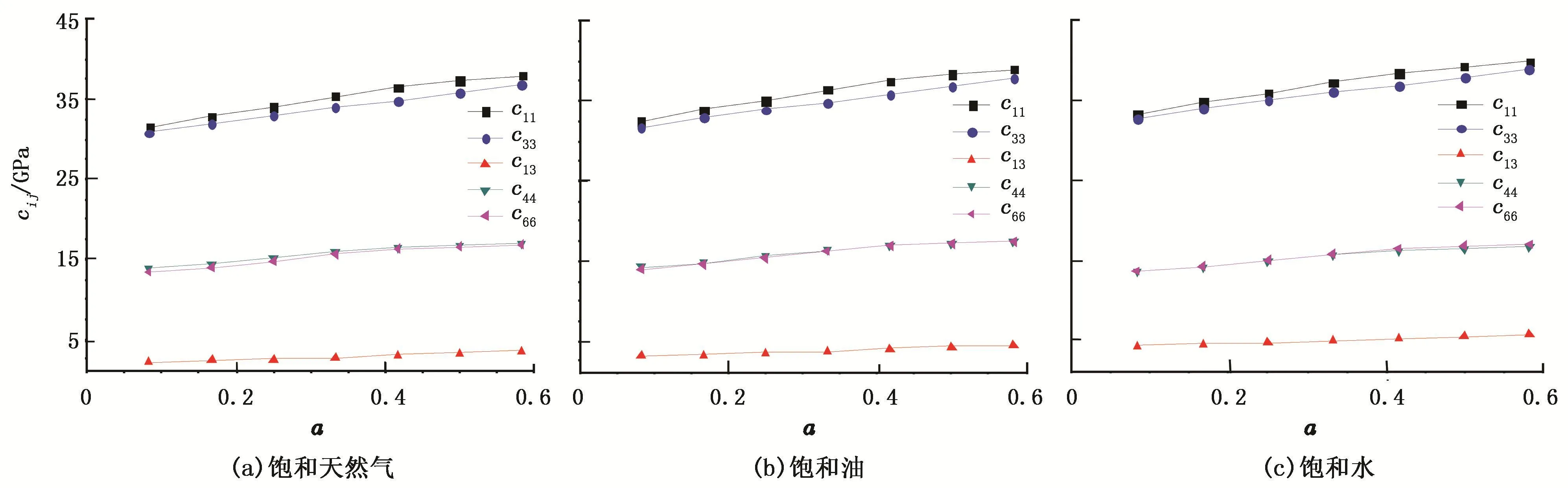
图7 刚度矩阵元素与裂缝纵横比的关系Fig.7 Relationship between stiffness matrix and crack aspect ratios
便士形状裂缝的纵向半轴a1的2倍对应裂缝的开度h,横向半轴a2的2倍对应裂缝的长度l。图7为裂缝长度为48 μm,裂缝中分别饱和天然气、油和水,通过改变裂缝开度得到的不同裂缝纵横比情况下CJ157数字岩心的刚度矩阵元素变化图。计算过程中天然气的体积模量为0.2 GPa,油的体积模量为1.02 GPa,水的体积模量为2.2 GPa。从图中可以看出,随着裂缝纵横比的增大,刚度矩阵元素均呈线性增大。
图8为裂缝开度为6 μm,裂缝长度为48 μm,不同裂缝密度情况下CJ157数字岩心的刚度矩阵元素变化图。从图中可以看出,随着裂缝密度的增大,刚度矩阵元素也呈线性减小。
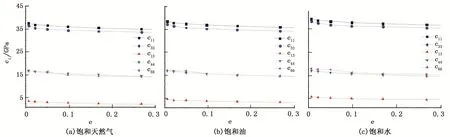
图8 刚度矩阵元素与裂缝密度的关系Fig.8 Relationship between stiffness matrix and crack density
4 结 论
(1)采用扩展的有限元方法计算的裂缝性低渗透储层弹性参数和理论计算结果基本吻合,验证了所扩展的数值模拟算法用于横向各向同性介质弹性性质研究的可行性。
(2)当裂缝纵横比和密度保持不变,流体模量为0时,纵波各向异性参数ε最大;随流体体积模量的增加,纵波各向异性参数ε呈线性减小。
(3)裂缝密度和流体性质保持不变,随裂缝纵横比增加,裂缝性低渗透储层岩石的弹性模量均呈线性增大。
(4)裂缝纵横比和流体性质保持不变,随裂缝密度增加,裂缝性低渗透储层岩石的弹性模量呈线性减小。
[1] 曾联波.低渗透砂岩储层裂缝的形成与分布[M].北京:科学出版社,2008.
[2] HAN D H.Effects of porosity and clay content on acoustic properties of sandstones and unconsolidated sediments [D].Standford:Standford University,1986.
[3] HASHIN Z,SHTRIKMAN S A.variational approach to the theory of the elastic behaviour of multiphase materials [J].J Mech Phys Solids,1963,11(2):127-140.
[4] BERRYMAN J G.Mixture theories for rock properties,in a Handbook of physical Constants[M].Washington:A-merican Geophysical Union,1995:205-228.
[5] BERRYMAN J G.Effective medium theories for multicomponent poroelastic composites[J].Journal of Engineering Mechanics,2006,132(5):519-531.
[6] CLEARY M P,CHEN I W,LEE S M.Self-consistent techniques for heterogeneous media[J].J Eng Mech, 1980,106(5):861-887.
[7] NORRIS A N.A differential scheme for the effective moduli of composites[J].Mech Mater,1985,4:1-16.
[8] ZIMMERMAN R W.Compressibility of sandstones[M]. New York:Elsevier,1991.
[9] BERRYMAN J G.Single-scattering approximations for coefficients in Biotıs equations of poroelasticity[J].J Acoust Soc Am,1992,91(2):551-571.
[10] KNACKSTEDT M A,ARNS C H,PINCZEWSKIZ W V, et al.Computation of linear elastic properties from microtomographic images:methodology and agreement between theory and experiment[J].Geophysics,2002,67 (5):1396-1405.
[11] ROBERTS A P,GARBOCZI E J.Computation of the linear elastic properties of random porous materials with a wide variety of microstructure[J].Proceedings of the Royal Society of London,2002,458:1033-1054.
[12] DINA M,BORIS G,RADIM C,et al.Finite element modelling of the effective elastic properties of partially saturated rocks[J].Computers&Geosciences,2008, 34(6):647-657.
[13] DUNSMOIR J H,FERGUSON S R,DıAMICO K L,et al.X-ray microtomography:a new tool for the characterization of porous media[R].SPE22860,1991.
[14] 康志勤,赵阳升,孟巧荣,等.油页岩热破裂规律显微CT实验研究[J].地球物理学报,2009,52(3): 842-848. KANG Zhi-Qin,ZHAO Yang-Sheng,MENG Qiao-Rong,et al.Micro-CT experimental research of oil shale thermal cracking laws[J].Chinese Journal of Geophysics,2009,52(3):842-848.
[15] DONG H,TOUATI M,MARTIN J B.Pore network modeling:analysis of pore size distribution of arabian core samples[R].SPE105156,2007.
[16] GASSMANN F.Uber die elastizitat porous media[J]. Vier der Natur Gesellschaft in Zurich,1951,96(1):1-23.
[17] THOMSEN L.Weak elastic anisotropy[J].Geophysics,1986,51:1954-1966.
(编辑 修荣荣)
Research of influence laws of fluid properties on elastic parameters of fractured low permeability reservoir rocks based on digital core
SUN Jian-meng1,YAN Guo-liang2,JIANG Li-ming3,CUI Li-kai1,ZHAO Jian-peng1,CUI Hong-zhu4
(1.School of Geosciences in China University of Petroleum,Qingdao 266580,China; 2.Research Institute of Petroleum Exploration&Development-Northeast,PetroChina,Lanzhou 730020,China; 3.Technology Center,China Petroleum Logging Company Limited,Xiıan 710077,China; 4.Changqing Division,China Petroleum Logging Company Limited,Xiıan 710077,China)
In order to investigate the effects of fracture and fluid properties on the elastic parameters of fractured low permeability reservoirs,the digital cores of low permeability reservoirs were constructed by X-ray CT.The transversely isotropic digital cores with parallel penny shape cracks were firstly constructed using digital image processing technology,then the elastic parameters of the cores were calculated by an extended finite element method,and lastly the effects of fracture and fluid properties on the elastic modulus were studied.The results show that with fixed crack aspect ratio and density,the longitudinal wave anisotropy linearly decreases with the increase of the fluid bulk modulus.With fixed crack density and fluid properties, the elastic moduli of fractured low permeability reservoir rock show a linear relationship with increasing crack aspect ratio. And with fixed crack aspect ratio and fluid properties,the elastic moduli of fractured low permeability reservoir rock show a linear relationship with increasing crack density.
well logging;fractured low permeability reservoir;rock properties;elastic modulus;digital core;finite element method
TE 19
:A
1673-5005(2014)03-0039-06
10.3969/j.issn.1673-5005.2014.03.006
2013-10-05
国家自然科学基金项目(41374124);国家重大科技专项(2011ZX05006-002)
孙建孟(1964-),男,教授,博士生导师,从事测井资料处理、解释与岩石物理研究。E-mail:sunjm@upc.edu.cn。
——以双河油田Eh3Ⅳ5-11岩心为例

