线性唯象传热时不可逆卡诺制冷机的生态学最优性能
朱小芹,眭永兴
(江苏理工学院数理学院,江苏 常州 213001)
0 引言
自上世纪七十年代以来,许多学者用有限时间热力学方法分析研究了热力系统的性能优化问题[1-4]。Angulo—Brown[5]在研究热机时证明,热机循环熵产率σ与低温热源温度TL之积TLσ反映了热机的功率耗散,故以式

为目标讨论热机的性能优化,P为输出功率。由于E目标在一定意义上与生态学的长期目标有相似性,故称其为“生态学”最优性能[6-9]。因为没有注意到能量(热量)与(功)的本质区别,式(1)隐含了矛盾,即将功率()与非损失放在一起作了比较是不完备的,文献[9]对此作出了订正。陈林根等[10]基于分析的观点,建立了各种热力循环统一的分析生态学目标函数为

对制冷机而言
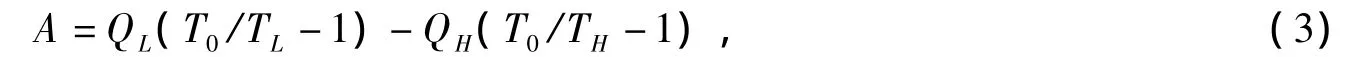
式中为QL吸热量,QH为放热量,TH、TL分别为高、低温热源温度。因为制冷系数 ε =QL/(QH- QL),制冷率 R=QL/τ,故有[10]
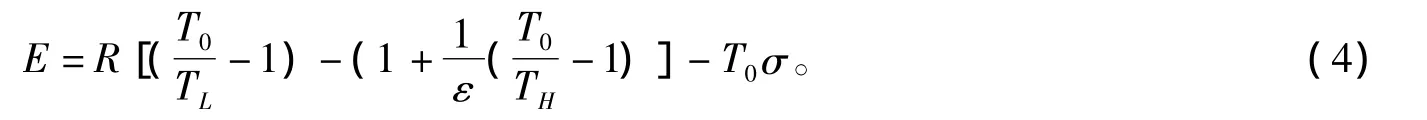
此后,不少文献讨论了牛顿传热规律下内可逆和不可逆卡诺热机[11-16]、制冷机[17]和热泵[18]的生态学性能,还有一些学者研究了 Brayton[19-21]、Stirling 和 Ericsson[22]热机,Brayton[23-24]和 Ericsson[25]制冷机,内可逆[26-27]、不可逆[28]简单空气热泵和回热式空气热泵[29-30],不可逆布雷森循环[31]的生态学性能。但实际热机、制冷机和热泵中工质与热源间的传热并非都服从牛顿(线性)定律。一些文献研究了传热规律(包括线性唯象传热规律 Q∝Δ(T-1),辐射传热规律 Q∝Δ(T4),Dulong—Petit传热规律 Q∝Δ(T1.25),广义对流传热规律Q∝Δ(T)m和广义辐射传热规律Q∝Δ(Tm)对内可逆和不可逆卡诺热机[32-37]、制冷机和热泵生态学性能的影响[38-41],文献[42]研究了复杂传热规律下内可逆正反向两热源循环的生态学最优性能,本文将进一步研究线性唯象传热时不可逆卡诺制冷机生态学最优性能,研究结果对实际制冷机的设计工作具有理论指导意义。
1 制冷机模型
如图1所示的制冷机满足以下四个条件:
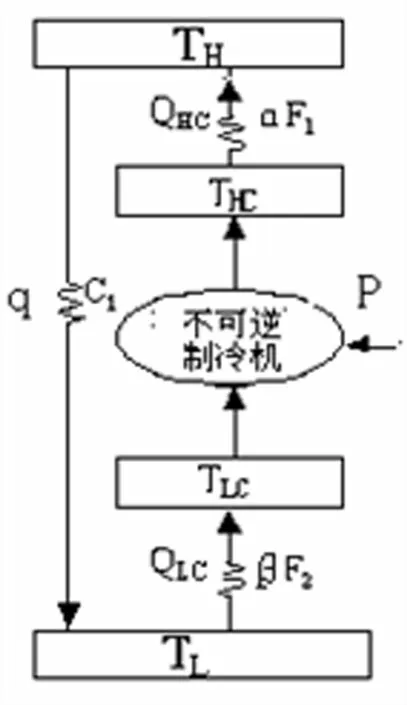
图1 不可逆制冷机模型
(1)制冷机中工质作定常态连续流动,循环由两个等温和两个绝热过程组成。
(2)由于热阻的存在,工质的吸、放热温度TLC,THC,不同于低,高温热源温度TL,TH且有

传热规律满足线性唯象传热规律Q∝Δ(1/T)。
换热器换热面积有限,高、低温侧换热器面积F1与F2之和为常数F,即有

(3)两热源间存在常数为q=Ci(1/TL-1/TH)的热漏流率(Ci为热漏系数)。设工质通过高、低温侧换热器交换吸放热流率为QHC、QLC,则实际高温热源的供热率QH和低温热源的吸热率QL分别为

(4)除热阻、热漏外,制冷机中还存在其它的不可逆性。因此,在相同的制冷率R下,进行这样的循环时,不可逆制冷机要比仅有热阻时的制冷机多输入一部分功率,所以在相同的R下,高温侧换热器中工质的放热率QHC就大于仅存在热阻损失时的放热率QHC,引进不可逆因子Φ

表示制冷机中除热阻和热漏外的其它不可逆性,如摩擦、涡流和非平衡等各种不可逆效应,显然,在以上模型中,若q=0且Φ=1,即为内可逆模型;若q>0但Φ=1,即为热阻加热漏模型;若q=0但Φ>1即为热阻加内不可逆模型。
2 最优特性关系
根据以上模型,由热力学第二定律,当循环中仅有热阻时,有

由(9)和(10)式有

由热力学第一定律,
制冷系数

制冷率

设传热服从线性唯象定律:

α、β分别为工质与热源间的传热系数(α、β均小于零),F1、F2为高、低侧换热器的传热面积,定义面积比f和工质温比x,

由(7)~(17)知
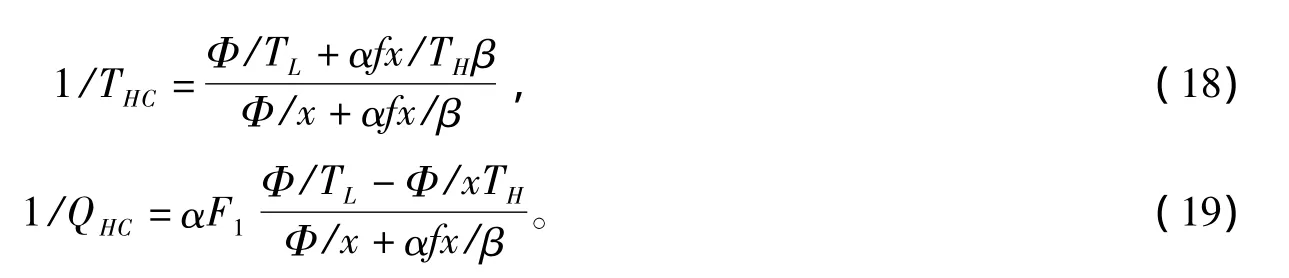
由(12)~(19)式可得

式中 aL=2T0/TL-1,aH=2T0/TH-1。
可见E、σ、R、ε均为面积比f和温比x的函数,由dE/df=0、dη/df=0或dR/df=0均可得当f=f0=(Φβ/α)0.5/x时,有一定温比x下制冷机的最佳制冷率、最佳制冷系数、最佳熵产率和最佳E目标值:

式中,B= βF/[1+(βΦ)0.5/xα0.5]2。
3 讨论
(1)若q=0且Φ=1,即为内可逆模型;则(24)~(27)式变为

式中 B1= βF/[1+(β/α)0.5/x]2。
(2)若q=0但Φ>1,即为热阻加内不可逆模型,则(24)~(27)式变为:


(3)若q>0但Φ=1,即为热阻加热漏模型,则(24)~(27)式变为:
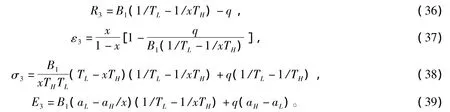
(4)由(27)式可知,最佳E目标值与x之间有极值关系,由dE/dx=0知,当x=xE,
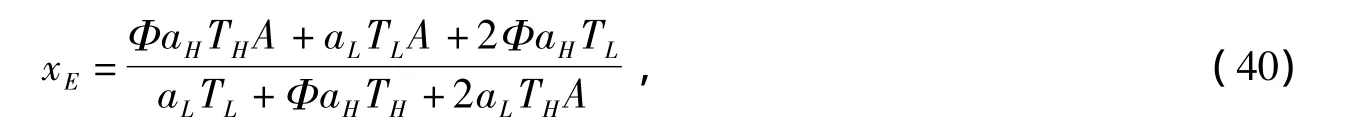
(A=(βΦ/α)0.5)时,E 有最大值 Emax,

将此xE代入(23)-(25)式可得对应于最大E目标值时的制冷率RE、制冷系数εE和熵产率σE。由dσ/dx=0 可知,当 x=xσ,
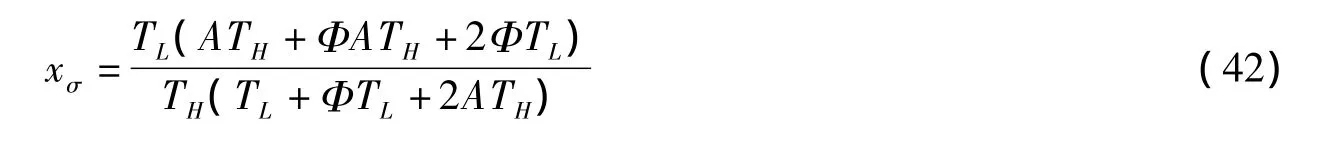
时σ取最小值σmax,

将此xσ代入(23)、(24)及(26)式可得对应于最小熵产率时的制冷率Rσ、制冷系数εσE目标值Eσ。
同理可求得 xE及相应的 εmax、Rε、σε和Eε,这里不作赘述。

图2 不同参数下E与ε的关系

图3 不同参数下E与R的关系
取 α=β,αF=400 000kW/K,TH=300K,TL=260K,T0=290K,Φ =1.0~1.2,Ci=0~400kW/K 进行计算。图2、图3分别给出了不同Φ及Ci下制冷机生态学E目标值与制冷系数、制冷率的关系曲线。图2表明:内可逆制冷机生态学E目标值随制冷系数的变化呈抛物线型,随着不可逆因子的增加,E目标值明显下降,但曲线的抛物线形状不变,除了最大目标点之外,对应于某一E目标值,有两个制冷系数ε值,但热漏对生态学E目标值的影响则从根本上把曲线的抛物线形状改变为扭叶型,可见热漏q与不可逆因子Φ对制冷机生态学E目标值的影响效果截然不同。由图3可知,生态学E目标值随制冷率的变化呈抛物线型,除了最大E目标点之外,对应于某一E目标值,制冷率R有两个值,我们应使制冷机工作于R较大的状态点,E目标值随着不可逆因子的增加而下降,热漏对制冷机的影响也呈类似变化。

图4 生态学目标、熵产率输出及制冷率与制冷系数的关系
4 结论
本文用生态学优化方法,综合考虑热阻、热漏及其它内不可逆性对线性唯象传热规律下不可逆卡诺制冷机性能的影响,导出了Q∝Δ(1/T)时不可逆卡诺制冷机机的生态学最优性能,并由数值算例对不同损失情况下的制冷机性能变化规律进行了比较,得到的一系列关系曲线有助于更深入了解热阻、热漏、内不可逆性对制冷机性能的影响规律,本文结果给制冷机设计提供了一个最优的折衷备选方案。
[1]Bejan A.Entropy generationminimization:The new thermodynamics of finite - size device and finite - time processes[J].J.Appl.Phys.,1996,79(3):1 191 -1 218.
[2]Chen L,Wu C,Sun F.Finite time thermodynamic optimization or entropy generationminimization of energy systems[J].J.Non - Equilib.,Thermodyn.,1999,24(4):327 -359.
[3]Wu C,Chen L,Chen J.Recent Advances in Finite - Time Thermodynamics[M].New York:Nova Science Publishers,1999.
[4]陈林根,孙丰瑞,Wu Chih.有限时间热力学理论和应用的发展现状[J].物理学进展,1998,18(4):395-422.
[5]Angulo - Brown F.An ecological optimization criterion for finite - time heat engines[J].J.Appl.Phys.,1991,69(11):7465-7469.
[6]陈林根,孙丰瑞,陈文振.传热时有限时间热机的生态学最优性能[J],燃气轮机技术,1995,8(1):16-18.
[7]Cheng C Y,Chen C K.The ecological optimization of an irreversible Carnot heat engine[J].J.Phys.D:Appl.Phys.,1997,30(11):1 602-1 609.
[8]Cheng C Y,Chen C K.Ecological optimization of an endoreversible Brayton cycle[J].Energy Convers.Mgm t.,1998,39(1/2):33-44.
[9]Yan Z.Comment on“ecological optimization criterion for finite - time heat engines”[J].J.Appl.Phys.,1993,73(7):3 583.
[10]陈林根,孙丰瑞,陈文振.热力循环的生态学品质因素[J].热能动力工程,2002,17(2):172-175.
[11]Cheng C,Chen C.The ecological optimization of an irreversible Carnot heat- engine[J].JPhys D:Appl Phys,1997,30(11):1 602-1 609.
[12]Chen L,Zhou J,Sun F,et a1.Ecological optimization for generalized irreversible Carnot.Engines[J].Appl Energy,2004,77(3):327-338.
[13]Xia D,Chen L,Sun F,et a1.Universal ecological performance for end0reversible heat engine cycles[J].Int JAmbient Energy,2006,27(1):15 -20.
[14]Zhang W,Chen L,Sun F,eta1.Exergybased ecological optimal performance for a universalendoreversible thermodynamic cycle[J].Int.J.Ambient Energy,2007,28(1):51 -56.
[15]Chen L,Zhang W,Syb F.Power,efficiency,entropy generation rate and ecologicaloptimization for a class of generalized irreversible universal heat engine cycles[J].Appl Energy,2007,84(5):512 -525.
[16]UST Y,SAHIN B,KODAL A.Ecological coefficient of performance(EC0P)optimization for generalized irreversible Carnot heat engines[J].JEnergy Inst,2005,78(3):145 -151.
[17]朱小芹,陈林根,孙丰瑞,广义不可逆制冷机的生态学最优性能[J].低温与超导,2004,32(3):61-64.
[18]Chen L,Zhu X,Sun F,et a1.Exergy - based ecological optimization for a generalized irreversible Carnot heat pump[J].Appl.Energy,2007,84(1):78 -88.
[19]Cheng C,Chen C.Ecological optimization of an endoreversible Brayton cycle[J].Energy Convers.Mgmt,1998,39(1/2):33-44.
[20]TYAGIS,KAUSHIK S.Ecological optimization of an irreversible regenerative intercooled Brayton heat engine with direct heat loss[J].Int.J.Ambient Energy,2005,26(2):81 -92.
[21]UST Y,SAFA A,SAHIN B.Ecological performance analysis of an endoreversible regenerative Brayton heat—engine[J].Appl.Energy,2005,80(3):247 -260.
[22]TYAGIS,KAUSHIK S,SALHOTRA R.Ecologica1 optimization and performance study of irreversible Stirling and Ericsson heat engines[J],Phys.D:Appl.Phys.,2002,35(20):2 668 -2 675.
[23]Tu Y,Chen L,Sun F,eta1.Exergy - based ecologicaloptimization for an endoreversible Brayton refrigeration cycle[J].Int JExergy,2006,3(2):191 -201.
[24]屠友明,陈林根,孙丰瑞.内可逆空气制冷机的生态学优化性能[J].热科学与技术,2005,4(3):199-204.
[25]TYAGIS,CHEN J,LIN G,et a1.Ecological optimization of an irreversible Ericsson cryogenic refrigerator cycle[J].Int J Energy Res,2005,29(13):1 191 -1 204.
[26]BIY ,Chen L,Sun F.Comparative performance analysis for endoreversible simple air heatpump cycles considering ecological,exergetic efficiency and heating load objectives[J].Int JExergy,2009,6(4):550 -566.
[27]BIY ,Chen L,Sun F.Ecological,exergetic efficiency and heating load optimizations for endoreversible variable - temperature heat reservoir simple air heat pump cycles[J].Int JLow - Carbon Tech,2010,5(1):7 -17.
[28]BIY,Chen L,Sun F.Ecological,exergetic efficiency and heating load optimizations for irreversible variable - temperature heat reservoir simple air heat pump cycles[J].Indian Jof Pure and Appl.Phys,2009,47:852 -862.
[29]BIY,Chen L,Sun F.Exergy based ecological optimization for an endoreversib1e variable - temperature heat reservoir air heat pump cycle[J].Revista Mexicana de Fisica,2009,55(2):l12 -119.
[30]BIY,Chen L,Sun F,et a1.Exergy - based ecological optimization for an endoreversible air heat pump cycle[J].Int.J.Ambient Energy,2009,30(1):45 -52.
[31]贺 星,陈林根,孙丰瑞.具有热阻、热漏的不可逆布雷森循环生态学性能新析[J].热科学与技术,2009,8(2):140-145.
[32]杨博,陈林根,孙丰瑞.线性唯象传热规律下广义不可逆卡诺热机生态学性能系数优化[J].热科学与技术,2010,9(1):43-50.
[33]朱小芹,陈林根,孙丰瑞.Q∝(ΔT-1)时不可逆卡诺热机的生态学性能优化[J].扬州大学学报:自然科学版,2004,7(1):13-16.
[34]李俊,陈林根,戈延林,等.内可逆正反向两热源循环复杂传热规律下生态学最优性能[J].热科学与技术,2013,12(3):228-235.
[35]朱小芹,陈林根,孙丰瑞.Q∝(ΔT)n时广义不可逆卡诺热机的生态学性能优化[J].东南大学学报:自然科学版,2004,34(3):414 -417.
[36]Zhu X,Chen L,Sun F,et a1.Effect of heat transfer law on the ecological optimization of a generalized irreversible Carnot engine[J].Open Sys.& Inform.Dyn.,2005,12(3):249 -260.
[37]沈大华.Q∝(ΔTn)时不可逆卡诺制冷机的生态学性能优化[J].武汉科技大学学报:自然科学版,2004,27(4):434-436.
[38]朱小芹,陈林根,孙丰瑞.Q∝(ΔT)n时广义不可逆卡诺制冷机的生态学最优性能[J].低温与特气,2006,24(2):10-13.
[39]屠友明,陈林根,孙丰瑞,内可逆空气制冷机性能的生态学优化[J].热科学与技术,2005,4(3):199-204.
[40]Zhu X,Chen L,Sun F ,et a1.Effect of heat transfer law on the ecological optimization of a generalized irreversible Carnot heat pump[J].Int.J.Exergy,2005,2(4):423 - 436.
[41]Zhu X,Chen L,Sun F,et a1.The ecological optimization of a generalized irreversible Carnot heat pump for a generalized heat transfer law[J].JEnergy Inst.,2005,78(1):5 -10.
[42]李俊,陈林根,戈延林,等.内可逆正反向两热源循环复杂传热规律下生态学最优性能[J].热科学与技术,2013,12(3):228-235.

