关于二维连续型随机变量函数分布的推广和运算

刘 淼

(伊犁师范学院数学与统计学院，新疆伊宁 835000)

关于二维连续型随机变量函数分布的推广和运算

刘 淼

(伊犁师范学院数学与统计学院，新疆伊宁 835000)

本文从二维连续型随机变量的联合分布函数与联合概率密度函数的关系入手，讨论了二维连续型随机变量四则运算的分布，并给出了求解函数分布的简便方法。

连续型随机变量；分布函数；密度函数

1 预备知识

定义1 对于二维随机变量(ξ，η)，对任意实数x,y，称函数F(x,y)=P{ξ≤x,η≤y}称为(ξ,η)的分布函数，或称为随机变量(ξ,η)的联合分布函数[1-2].

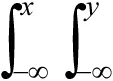
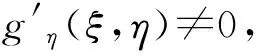
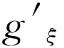
2 主要结果

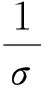
定理2 设F1(x),F2(x),…,Fn(x)分别是n个分布函数，则存在不全为零的ai≥0,(i=1,…,n)，且当a1+a2+…+an=1时，F(x)=a1F1(x)+a2F2(x)+…+anFn(x)为某一连续型随机变量分布函数．

证明 先任取一组不全为零的ai≥0,(i=1,…,n)，且有a1+a2+…+an=1.

根据条件F1(x),F2(x),…,Fn(x)均是分布函数，故F1(x),F2(x),…,Fn(x)都满足非递减、右连续等性质，且有F1(+∞)=F2(+∞)=…=Fn(+∞)=1，F1(-∞)=F2(-∞)=…=Fn(-∞)=0，

从而F(x)=a1F1(x)+a2F2(x)+…+anFn(x)非递减且右连续，

又由于F(+∞)=a1F1(+∞)+a2F2(+∞)+…+anFn(+∞)=1，

F(-∞)=a1F1(-∞)+a2F2(-∞)+…+anFn(-∞)=0，

则由连续型随机变量的分布函数定义的性质可得，一定存在不全为零的非负实数a1,a2,…,an且a1+a2+…+an=1，使得F(x)=a1F1(x)+a2F2(x)+…+anFn(x)为某一随机变量的分布函数．

定理3 设F1(x),F2(x),…,Fn(x)是分布函数，则存在不全为零的非负连续函数a1(x),a2(x),…,an(x),…,x∈(-∞,+∞)，则a1(+∞)+a2(+∞)+…+an(+∞)=1，且a1(+∞)+a2(+∞)+…+an(+∞)=1，使得F(x)=a1(x)F1(x)+a2(x)F2(x)+…+an(x)Fn(x)为分布函数．

此定理的证明由定理2可直接推出.

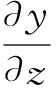
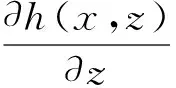
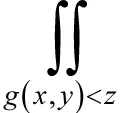
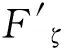
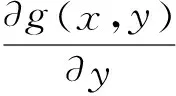
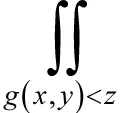
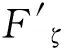
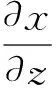
根据定理4和定理5可知，对于x或y的单调函数可通过利用其中一个变量来替换另一个变量，进而将多重积分转化成只对x或y的积分，使得整个积分过程变得简单.根据上述定理，显然有二维连续型随机变量的和、差、积、商的分布分别为:

3 应用举例

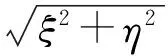
解 当ζ<0时，fζ(z)=0显然成立.

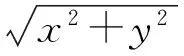
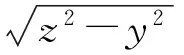
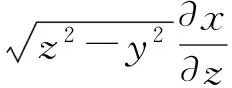
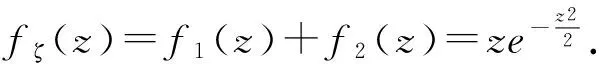
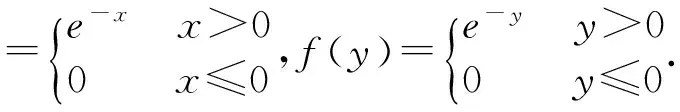
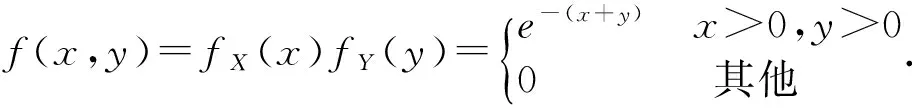
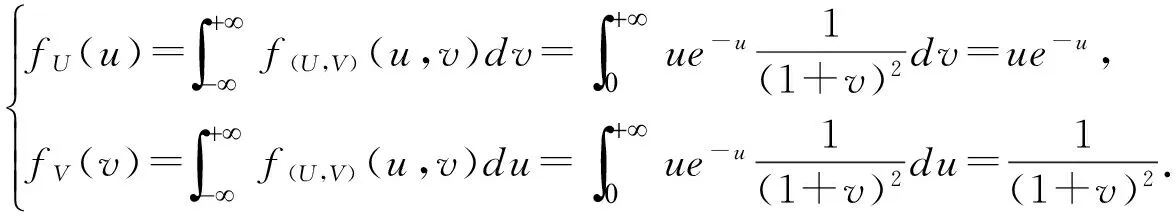
所以f(U,V)(u,v)=fU(u)fV(v)，从而U,V相互独立.

例3 设f(x,y)为二维连续型随机变量(ξ,η)的联合概率密度函数，且(ξ,η)相互独立，令U=ξ-η，试求连续型随机变量U的概率密度函数fU(u).

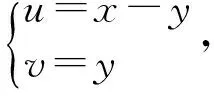
则根据定理1，有f(U,V)(u,v)=f(ξ,η)[x(u,v),y(u,v)]|J|=f(u+v,v)，又由于U=ξ-η，

[1]魏宗舒.概率论与数理统计[M].北京:高等教育出版社,2003.

[2]李贤平.概率论基础[M].北京:高等教育出版社,2006.

[3]唐小峰.连续型随机变量独立性的几个充要条件[J].阜阳师范学院学报:自然科学版,2010(2):24-27.

[4]吕洪升,张千祥.二维连续型随机变量相关计算的积分限确定问题[J].大学数学,2012(3):194-199.

[5]Barr,D.R.and Darling,D.A.,A.Kolmogorov-Smirnov Test for Gensored samples[J].Techn-ometrics,1999(15):739-757.

[6]Finklestein,J,M.and Schafer,R.E.Improved goodness of Fit Tests[J].Biometrika,2007(58):641-645.

The Promotion and Operation of the Function Distribution of the Two-dimensional Continuous Random Variable

LIU Miao

(School of Mathematics and Statistics，Yili Normal University, Yining Xinjiang 835000,China)

In this paper, we mainly discussed the distribution of two-dimensional continuous random variable four operation through the relation between distribution function and probability density function, and then researched the method of finding the function distribution of common two-dimensional continuous random variables.

continuous random variable; distribution function; density function

2013-12-07

国家自然科学基金项目(11161050)；新疆维吾尔自治区重点学科(基础数学)开放课题(2012ZDXK09)；伊犁师范学院2012年一般科研项目(2012YB015)。

刘 淼(1976- )，男，山东郓城人，伊犁师范学院数学与统计学院副教授，硕士生导师，从事概率论与数理统计研究。

O211

A

1008-178X(2014)01-0001-03