纵向磁化铁氧体基片上微带线的特性分析

杨林颖，刘建美

（1.山东科技大学 电子通信与物理学院，山东 青岛266590；2.莱州过西中学，山东 莱州261400）

0 Introduction

Devices and systems of microwave and millimeterwave are becoming increasingly important for both defense and commercial applications.For example，devices of reciprocal and nonreciprocal ferrite，such as circulators，isolators and phase shifters，are building blocks of high－performance phased－array radars and communication systems. Currently，these ferrite devices are used as discrete components in transmit／receive （T／R）modules and front－ends of phased－array radar are bulky and costly.The development of monolithic planar ferrite circuits are in great demand.It will considerably simplify the production process and reduce the component cost.Analysis of single－microstrip line on ferrite substrates provides guidance for the integrated assembly design of components on ferrite substrates.

The feature of ferrite material is that its permeability is a tensor，which always depends on the operating frequency and applies dc magnetic field.The result is achieved in great complexity of analysis and calculation.A number of papers have described the characteristics of microstrip on ferrite substrates.An approximate analysis was presented together with a physical description of the modes of propagation in stripline and microstrip devices of significant width，using ferrite slabs as dielectric material，magnetized perpendicular to the ground plane［1］.The dispersion characteristics of shielded microstrip lines on biased ferrite substrate were calculated in the quasi－isotropic approximation by a mode－matching procedure［2］.The analysis of microstrip lines on ferromagnetic and uniaxial anisotropic dielectric substrates was performed by using the Hertz vector potentials in conjunction with Galerkin’s procedure［3］.The normalized longitudinal and transverse current distributions of microstrip lines on ferrite substrates were obtained by using spectral－domain approach for vertical magnetization［4］.The spectral domain approach was used for full－wave determination of propagation constant and characteristic impedance of microstrip lines fabricated on ferrite substrates with arbitrarily oriented bias magnetic field［5］.Microstrip structures of dispersion diagrams，surface current，magnetic－field and electric－field distributions and Poynting－vector distributions were found containing a multilayered medium with a ferrite material layer using an anisotropic dyadic Green’s function［6］.

In this paper，characteristic impedance，the propagation and phase shift characteristics of microstrip lines fabricated on axially－magnetized ferrite substrates are compared by using analytic formulas that adequately describe the microwave properties of microstrip lines on ferrite substrates proposed in Ref.［7］.

1 Formulas of ferrite single－microstrip line（FSL）

The structure of FSL is illustrated in Fig.1，where a dc magnetic field H0is applied to parallel to the direction of propagation in the z－axis.In the biased configuration the tensor permeability of ferrite is expressed as

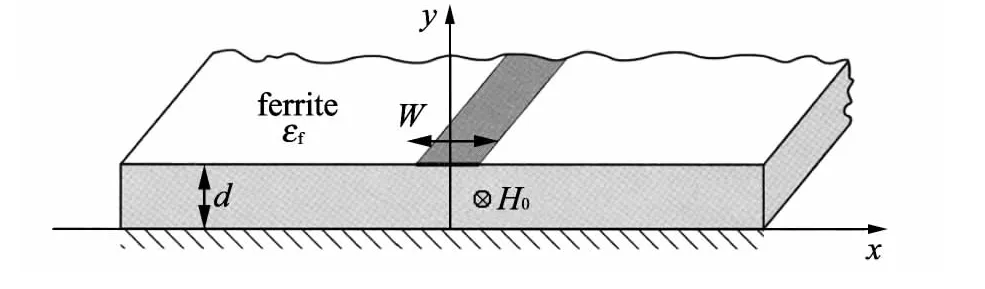
Fig.1 Single－microstrip line on ferrite substrates

For demagnetized substrates，the off－diagonal tensor elements vanish，i.e.，κ＝0.Schlomann has shown that the permeability tensor elementμ ＝μd can be approximated by the simple expression for the demagnetized state，that is

For a TEM approximation mode，the characteristic impedance Z0can be written as simple formula by considering the duality ofεandin Maxwell’s equations.It can be shown as［9］

where Z0（1）is the characteristic impedance of microstrip with air as the substrates.εeff（εf）andμeff（μ）are effective permeability and permittivity，respectively.They can be written as［7］

Phase shift per unit length is given asφ／L，and there is H0＞0for dc bias field.It is taken with respect to ferrite which is“just saturated”（H0＝0），i.e.［10］

2 Numerical results

Figs.2－3 illustrate the dispersion behaviours of the characteristic impedance Z0and the normalized propagation constant.It can be seen，for a given thickness of ferrite substrate，that the characteristic impedance Z0and the effective dielectric constant are larger if the strip width of micrstrip lines is widened.

Fig.2 Curves of characteristic impedance Z0of FSL

Fig.3 Curves of normalized propagation constant of FSL

For the sake of brevity，solutions for frequencies below resonance are not discussed here.The variations of propagation constantβ with H0in Fig.4 allow for the implementation of phase shifters with FSL structures.Due to axial magnetization，the phase shifter would have the same amount of phase shift in both forward and reverse directions.It can be seen that the dispersion curve undergoes a drastic change when its substrate changes from the isotropic（4πMs＝0）to the gyrotropic.It can also be shown that the cut－off frequencies are mainly a function of ferrite parameters rather than structures.

Fig.4 Normalized dispersion diagram of effects of H0

From Fig.5，it can be calculated that a line length of 58.5 mm would be required to achieve a phase shift up to 180°at 8 GHz on a microstrip of aspect ratio w／d＝2 with a maximum applied bias field H0of 800 Oe.It can be seen that the phase shift per unit length increase with widening strip width of the FSL structures because of increasing concentration of the RF magnetic field on ferrite substrates.

Fig.5 Phase shift per unit length for different w／d

Fig.6 Phase shift per unit length for different H0

Fig.6 shows that the phase shift per unit length has a wider bandwidth at higher frequencies，though the value of phase shift also falls as the frequency increases.Fig.7 shows that a better linearity of phase shift as a function of H0is also achieved at higher frequencies of FSL structure.A sufficient linear phase shifter may also be used as a phase modulator.

Fig.7 Phase shift per unit length at different f

3 Conclusion

The comparative study of microstrip on longitudinally－magnetized ferrite substrates has revealed that the characteristic impedance，propagation constant and phase shift per unit length increase with widening strip width of the microstrip structure.Greater bandwidth and better linearity are obtained at higher frequencies.The results can be used as the main references for most ferrite microstirp devices.

［1］Hines M E.Reciprocal and nonreciprocal modes of propagation in ferrite stripline and microstrip devices.IEEE Transactions on Microwave Theory and Techniques，1971，19（5）：442－451.

［2］Hofmann H.Dispersion of the ferrite－filled microstripline.Arch.Elektron.Uebertragungstech.，1974，28：223－227.

［3］Albuquerque M R M L，D’Assungao A G，Mais M R G.Full－wave anlysis of microstrip lines on ferrite and anisotropic dielectric substrates.IEEE Transactions on.Microwave Theory Techniques，1989，25（4）：2944－2946.

［4］Hindy M A，Mitkees A A，Elsohly A A.Application of convolution approach for microstrip lines on ferrite substrate.Microwave and Optical Tachnology Letters，1992，5（14）：742－745.

［5］Leon G，Boix R R，Medina F.Efficient full－wave characterization of microstrip lines fabricated on magnetized ferrites with arbitrarily oriented bias field.Journal of Electromagn Waves and Application，2001，15（2）：223－252.

［6］Krowne C M.Electromagnetic distributions demonstrating asymmetry using a spectral－domain dyadic green＇s function for ferrite microstrip guided－wave structures.IEEE Transactions on Microwave Theory Techniques，2005，53（4）：1345－1361.

［7］Yeo K S K，Lancaster M J.New model for the effective permeability of ferrite microstrip.High Frequency Postgraduate Student Colloquium，1999：105－110.

［8］Lax B，Button K J.Microwave ferrites and ferrimagnetics.New York：McGraw－Hill Book Company，1962.

［9］Pucel R A，Masse D J.Microstrip propagation on magnetic substrates－Part I：Design theory.IEEE Transactions on Microwave Theory and Techiques，1972，20（5）：304－308.

［10］Teoh C S，Davis L E.A comparison of the phase shift characteristics of axially magnetized microstrip and slotline on ferrite.IEEE？Transactions on Magnetics，1995，31（6）：3464－3466.