附等式约束线性模型的验后单位权中误差最小值的估算及其应用

谢波

(重庆水利电力职业技术学院，重庆 402160)

1 引言

在测量数据处理过程中，往往对待估的参数给予一定的先验约束条件，如果约束条件为等式约束，则称之为附等式约束线性模型。合理选择或增加先验约束能够改善解的质量［1，2］和使验后单位权中误差产生增益［3～5］。姚宜斌［3］从随机模型误差和函数模型误差两个方面，推导附加约束条件对平差结果的影响，并以平差后的验后单位权中误差减小为条件，分析附加额外约束产生精度增益的条件。刘根友等［4］将附有参数先验精度信息的平差问题扩展为参数约束平差，在数值上统一为自由网平差和附合网平差，得出一旦观测网形和观测方案确定，验后单位权方差是唯一的结论。邓兴升等［5］采用顾及先验信息的贝叶斯估计方法，通过设计虚拟观测值，推导顾及先验信息的平差函数模型和最优参数估计公式，得到先验精度和虚拟观测值的质量与平差精度之间的关系及单位权方差的计算式。

本文根据附等式约束线性模型参数估计的平差过程，利用正定二次型矩阵极值的方法，推导出附加等式约束平差系统的验后单位权中误差最小值，并用于平差系统的起算点兼容性检核，数据验算例子验证了作者结论的正确性。

2 附等式约束线性模型的验后单位权中误差最小值的估算

测量平差概括模型可以描述为［6］:

其中式(1)为误差方程，式(2)为等式约束方程，L为n×1观测向量，n为观测向量的个数，B为n×u系数矩阵，X为u×1未知参数向量，u为未知参数向量的个数，C为s×u系数矩阵，W为s×1约束向量，s为等式约束个数，V为n×1改正数向量，具有0均值与方差－协方差阵D(△)=σ2Q，Q=P－1是协因数矩阵，P是权矩阵。

当无等式约束时，参数估计:

单位权方差估值:

当附加等式约束时，参数估计:

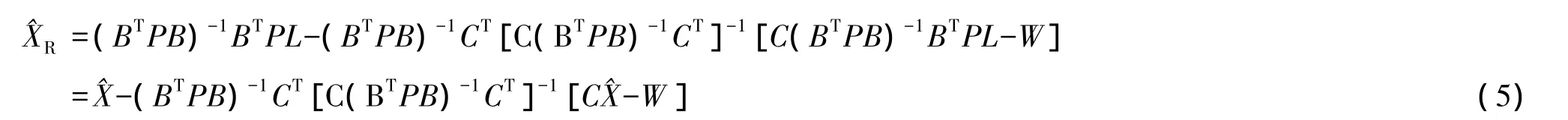
残差的二次型:

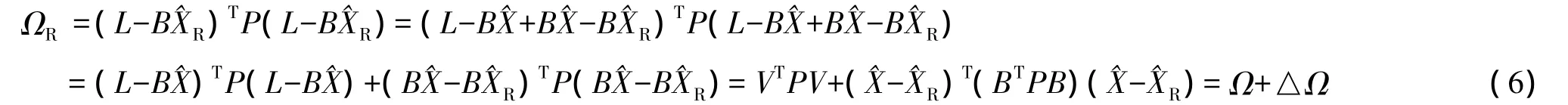
分析ΩR，其由两项组成，第一项是不受等式约束影响的，仅考虑第二项△Ω。

根据二次型矩阵的性质［7］:对 X∈Cn，A∈Hn×n，λu≤…≤λ2≤λ1是矩阵A的特征根，则λu|X|2≤XTAX≤λ1|X|2。

由于权阵P为对称正定矩阵，所以BTPB也是正定矩阵。根据正定矩阵的所有特征根都是正数的性质［8］，矩阵BTPB的特征根λmin＞0。所以，当且仅当或无等式约束的观测方程的参数估计满足等式约束方程，即 W=C(BTPB)－1BTPL 时，附等式约束线性模型的验后单位权中误差可以取得最小值:

上式和一般的测量平差概括模型的单位权中误差计算公式的区别在于V为无附加等式约束时的残差，u为无附加等式约束时未知参数的个数。

3 在起算点兼容性检验中的应用

如图1所示，A、B、C、D为已知点的测角网，观测值的个数为20，待定点为E、F点2个点。表1为原始观测值和对D点Y坐标添加 100 mm粗差的单位权中误差的计算结果。

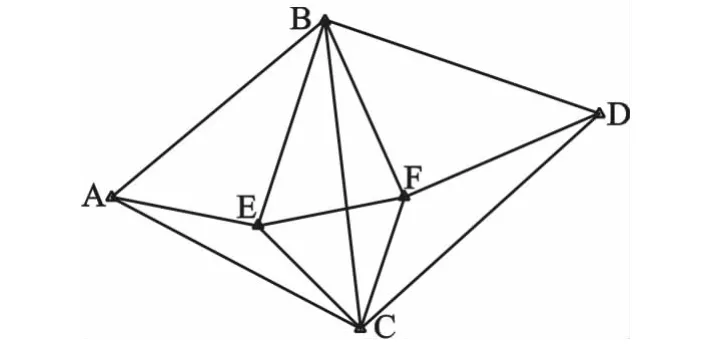
图1 测角网

数据分析表 表1

分析:

(1)当起算数据为2个点的坐标时，不论A、B、C、D是何种两点的组合，也无论D点Y坐标是否存在粗差，测角网的单位权中误差均为0.82 mm，VTPV=(n－u)=0.822×(20－8)=8.07。这是因为测角网的必要起算数据为2个点的坐标，当测角网仅有必要起算点时，该2点坐标为平差系统提供位置基准、方位基准和尺度基准，单位权中误差仅由观测值来确定。

(2)当已知点为3个起算点时，验后单位权中误差可以取得最小值

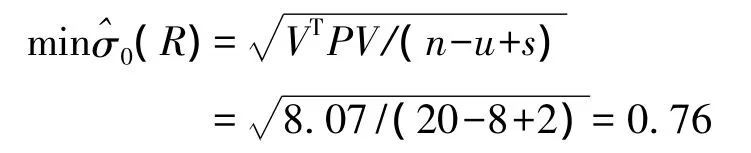
(3)当已知点为4个点时，验后单位权中误差可以取得最小值

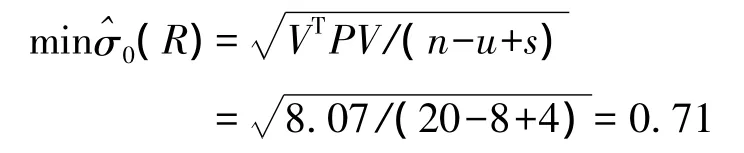
通过上述分析可以总结，判断起算点中不兼容点的步骤:

②起算点间兼容性好与差的判断。计算包含所有起算点的验后单位权中误差最小值，超出限差，则起算点间的兼容性较差。

③不兼容点的判断。在必要起算数据(点)个数基础上逐个增加起算点，计算增加起算点后的验后单位权中误差最小值，超出限差)的组合点中包括不兼容点，超限的组合点的共同点为不兼容点。

4 结论

(1)无等式约束的观测方程的参数估计满足等式约束方程时，可以使得等式附约束线性模型的验后单位权中误差的估值取得最小值，该最小值由无等式附加约束条件的观测方程、观测值的个数和约束条件的个数确定。

(2)附等式约束线性模型的验后单位权中误差最小值是测量系统的验后单位权中误差的“先验值”，在没有验前统计信息时，可以将其作为限差的基准值，在起算点兼容性检验中的应用之，该方法比应用方差检验的方法简单且可靠。

［1］欧吉坤.测量平差中不适定问题解的统一表达与选权拟合法［J］.测绘学报，2004，33(4):283～288.

［2］欧吉坤，王振杰.单频GPS快速定位中模糊度解算的一种新方法［J］.科学通报，2003，48(24):2572～2575.

［3］姚宜斌.GPS精密定位定轨后处理算法与实现［M］.武汉:武汉大学，2004.

［4］刘根友，郝晓光，柳林涛.参数约束平差法［J］.大地测量与地球动力学，2006，26(4):5 ～9.

［5］邓兴升，陈石桥，丁美青.顾及先验信息的变形监测网平差［J］.大地测量与地球动力学，2013，33(2):45～48.

［6］於宗俦，于正林.测量平差原理［M］.武汉:武汉测绘科技大学出版社，1990:127～130.

［7］王松桂，吴密霞，贾忠贞.矩阵不等式［M］.北京:科学出版社，2006:121～128.

［8］方保镕，周继东，李医民.矩阵论基础(第二版)［M］.南京:河海大学出版社，2003:108～111.