基于UMAC 的超精密研磨抛光机工件坐标系的建立

陈 琦

(中国科学院 长春光学精密机械与物理研究所，长春 130033)

0 引言

由于研制超精密陶瓷导轨的需要，本文用自主研发的超精密导轨研磨抛光机来实现对其加工。在陶瓷导轨后续超精密加工过程中需要频繁检测和研抛，由于陶瓷导轨工件的质量较大，在研磨抛光机和平面干涉仪之间来回搬动工件的过程中，陶瓷导轨在研磨抛光机上的每次定位很难保证完全一致。如果研磨抛光机基于机床坐标系来加工陶瓷工件的话，其定位精度不高。

现在对于开放式数控系统的研究越来越多［1-4］，加工的对象也是多种多样，对于某些特定的加工对象，基于机床坐标系的加工方式不能够完全满足要求，因此对于工件坐标系的研究与设计很有必要［5-10］。超精密导轨研磨抛光机数控系统基于UMAC 控制器，针对陶瓷导轨这种加工对象，采用基于机床坐标系与工件坐标系相结合的办法来实现运动控制。UMAC 控制器对于机床坐标系的建立相对容易，本文主要探讨UMAC控制器中工件坐标系的建立［11］。

1 UMAC 坐标系统

UMAC 中的坐标系统是一组(一个或更多)电机之间的同步运动。轴是坐标系统中的一个元素，通过使用比例因子和偏移量把它指派到一个电机上来实现。可命名的轴名称有直角坐标轴［X，Y，Z］、［U，V，W］和旋转轴［A，B，C］。一个坐标系统通过使用轴定义指令来建立，一个轴通过指派一个或多个电机来定义，电机映射到轴可以有比例因子也可以有原点偏移，比例因子代表每个单元多少编码器计数值。例如:#1→1000X +500 ，其中#1 代表1 号电机，1000 是比例因子，单位是counts/user unit，500 是偏移量，单位是counts。

在实际应用中，通过这种方法可以建立研磨抛光机的机床坐标系，由下式表示:

其中A1到A3是比例因子，B1到B3是偏移，#1 到#3 分别代表1～3 号电机。

2 坐标系转换

不同空间直角坐标系之间进行转换时，如图1 所示，当两个空间直角坐标系转换既有旋转又有平移时，则存在三个平移参数和三个旋转参数，再加上两个坐标系尺度变化参数m，总共有七个参数。相应的坐标变换公式为:

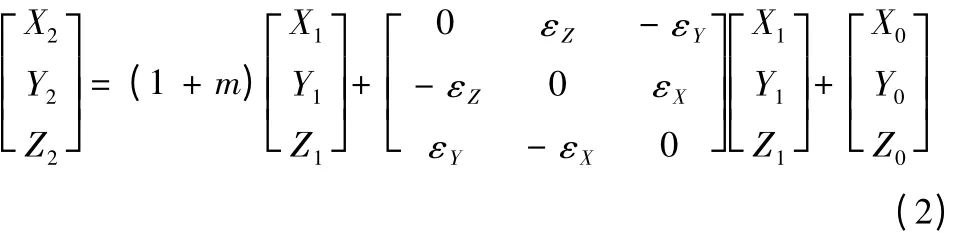
式(2)为两个不同空间直角坐标系之间的转换模型，其中含有7 个转换参数，为了求得7 个转换参数，至少需要3 个公共点，当多于3 个公共点时，可按最小二乘法求得各参数的最合适值。

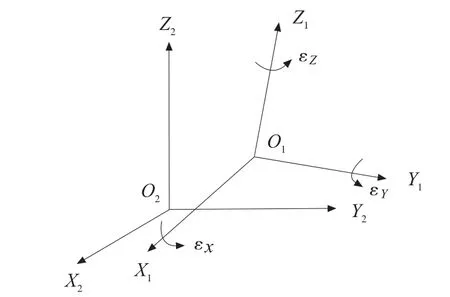
图1 不同空间直角坐标系之间转换

3 工件坐标系的建立

对于电机与直角坐标轴不完全一一对应的话，在UMAC 控制器中建立坐标系时，直角坐标轴可以是电机的线性组合，由下式表示:

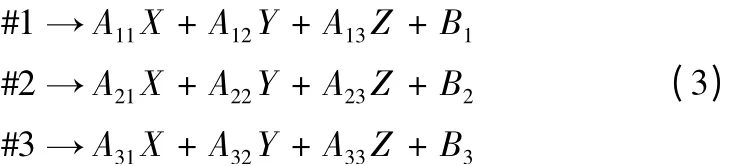
其中A11到A33是比例因子，B1到B3是偏移，#1 到#3 分别代表1～3 号电机。

研磨抛光机在实际应用过程中，首先采集工件坐标系中的三个特定点:原点O、X轴正向一点和XOY平面第一象限任意一点，通过原点O和X轴正向一点来确定X向的单位向量，然后结合XOY 平面第一象限任意一点来确定Y向的单位向量，最后通过X向、Y向和Z向三个单位向量的正交性来确定Z向的单位向量。

设采集的原点O为P1(x1，y1，z1)，采集的X轴正向一点为P2(x2，y2，z2)，采集的XOY 平面第一象限任意 一 点 为P3(x3，y3，z3)，设 点P1(x1，y1，z1)和 点P2(x2，y2，z2) 的 距 离 为OX， 得OX=设点P1(x1，y1，z1)和 点P3(x3，y3，z3)的 距 离 为OY，得OY =

由原点P1(x1，y1，z1)和X轴正向一点P2(x2，y2，z2)来确定X向的单位向量i=(ix，iy，iz)，得:

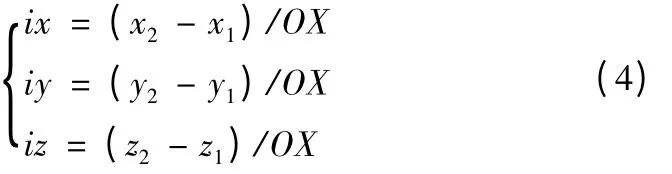
设P1P2和P1P3的夹角∠P2P1P3为∠XOY，结合XOY平面第一象限任意一点P3(x3，y3，z3)来确定Y向的单位向量j=(jx，jy，jz)，得:

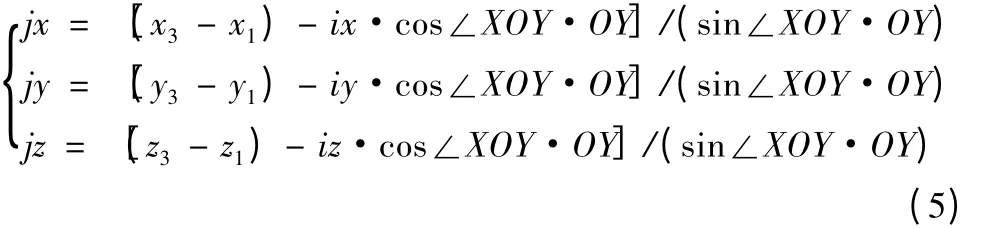
其中，

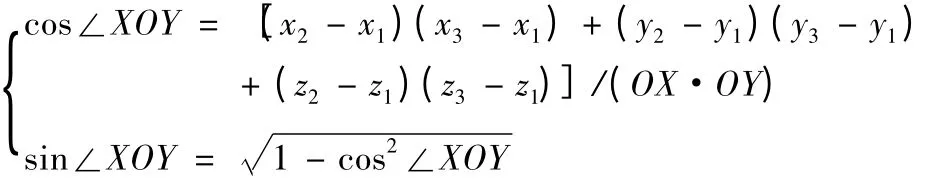
通过三个单位向量的正交性k=i·j 来确定Z向的单位向量k=(kx，ky，kz)，得

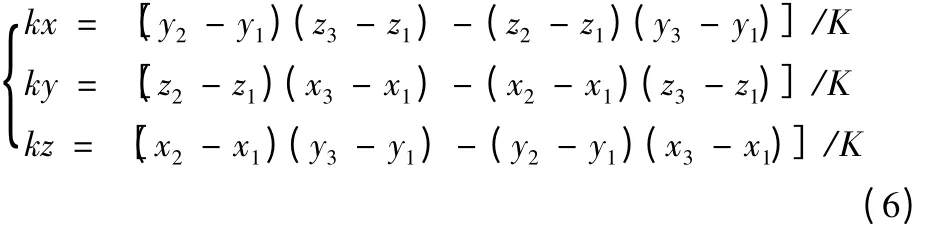
其中，

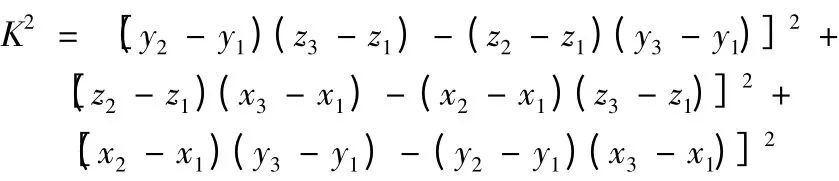
设陶瓷导轨上基于工件坐标系的某一点Pn的坐标为Pn(xn，yn，zn)，其在机床坐标系上的坐标为P'n(x'n，y'n，z'n)，两者之间关系如下:

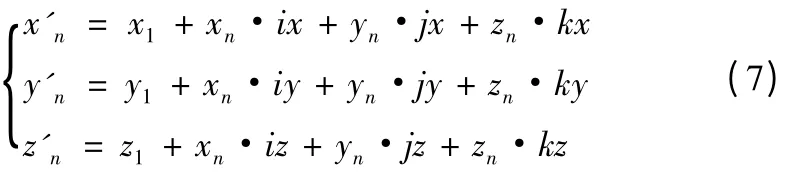
由此实现了陶瓷导轨上某点从工件坐标系到机床坐标系的转换。

研磨抛光机软件坐标转换模块如图2 所示，移动相关的轴使抛光头到达指定位置，分别点击软件界面中［取原点］、［X正向一点］和［XY面一点］，其三点的坐标值显示在左侧“工件坐标系”对应的数据框中，点击［计算单位向量］，计算出工件坐标系的单位向量，并显示在左侧“工件坐标系”对应的数据框中，在左侧“坐标系转换”中可以实现工件坐标系和机床坐标系的相互转换，输入工件坐标系各个坐标值，点击［工件→机床］，则机床坐标系显示出其对应的坐标值，输入机床坐标系各个坐标值，点击［机床→工件］，则工件坐标系显示出其对应的坐标值。

在实际应用过程中，当点击完界面中［取原点］、［X正向一点］和［XY面一点］确定好对应的三点后，点击［解坐标系］进行单位向量的计算，然后点击［打开数据］，该原始数据是基于工件坐标系的坐标值，直接把原始数据进行坐标转换，转换完后直接点击［下载运行］即可。

4 结束语

本文研制的研磨抛光机在实际应用过程中，首先采集陶瓷导轨在工件坐标系中的三个特定点:原点O、X轴正向一点和XOY 平面第一象限任意一点，通过这三个特定点正确的解算出工件坐标系与机床坐标系之间的转换关系。与公式(2)相比较，只需要采集三个点就能把机床坐标系转换成工件直角坐标系，非常实用和方便;而且不需要用最小二乘法求得各参数的最合适值，该方法计算值准确。若安装误差等原因导致研磨抛光机坐标轴的正交性不准确，采用该方法建立的工件坐标系不受其影响。该方法也适合应用在其他相关场合。

［1］彭玉海，白海清，何宁. 基于PMAC 运动控制卡的多轴开放式数控系统开发［J］. 机床与液压，2008，36(8):255 -257，251.

［2］尚纯，崔宝磊，杨光，等. 基于PMAC 的激光加工机床开放式数控系统开发［J］. 机床与液压，2013，41(19):83-85，124.

［3］李淑萍，张筱云. 基于PMAC 的开放式数控系统研究与应用［J］. 微电机，2009，42(7):65 -68，90.

［4］邴龙健，雷玉勇，蔡黎明，等. 基于PMAC 控制器的开放式数控系统研究［J］. 制造技术与机床，2009 (6):20-23.

［5］熊显文，明兴祖. 数控加工中心工件坐标系的建立［J］.组合机床与自动化加工技术，2003(12):69 -72.

［6］陈银清. 数控加工中工件坐标系的建立及其对刀技巧［J］. 煤矿机械，2004(4):78 -80.

［7］杨静云，李良仁. 数控加工中对刀设定工件坐标系的控制方法［J］. 组合机床与自动化加工技术，2009(5):72-74.

［8］祁型虹，熊显文，黄浙英. 建立数控工件坐标系的方法综述［J］. 机械设计与研究，2006，22(2):75 -78.

［9］张亚萍，曹燕. 三点圆法实现工件坐标系的自动设定［J］. 组合机床与自动化加工技术，2009(6):91 -92.

［10］刘源，韩振宇，王永章，等. 可配置型五坐标B 样条插补控制器的研制［J］. 光学精密工程，2010，18(7):1577-1585.

［11］刘恒丽，王太勇，王冬，等. 基于PMAC 的数控系统工件坐标系的设定方法分析［J］. 制造业自动化，2013，35(6):138 -140.