箱形钢梁双销轴连接承载性能分析
季 跃
(同济大学建筑设计研究院(集团)有限公司,上海200092)
1 引言
随着钢结构的推广应用,大型箱形钢梁越来越多地应用在实际工程中,特别是应用在大型结构安装施工的临时结构中。工程中的大型钢箱梁常采用工厂分段制作、施工现场拼装的施工方法[1,2]。目前,钢箱梁现场拼装的传统方法主要有高强螺栓连接、焊接连接和栓焊混合连接。若采用焊接拼接,在长期动荷载作用下焊接处易产生疲劳裂纹;若采用高强度螺栓拼接,当梁截面较大时,螺栓数量多,连接件净截面削弱较大,且螺栓受力不均,造价也高,同时制孔精度难以保证。此外,这两种传统连接方法均不能重复拆装,不适于施工用结构[3,4]。
针对钢梁拼接节点可拆装的要求以及目前拼接方式不足的问题,并结合施工企业的需要,本文参照国内外桥梁及机械结构构件连接中采用的销轴拼接方法,将双销轴连接应用于建筑钢结构特别是施工用可拆卸钢梁的拼接节点,形成一种新的建筑结构钢梁连接方式[5]。目前,这种销轴拼接的方法,除桥梁结构和机械工程外,国内建筑结构中尚未对此进行深入的理论分析与应用研究[6,7]。
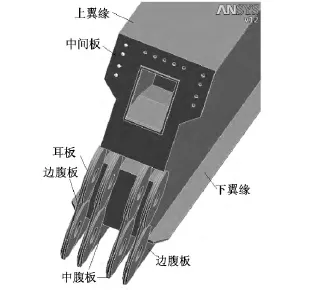
图1 梁段1示意图Fig.1 Schematic diagram of beam section 1
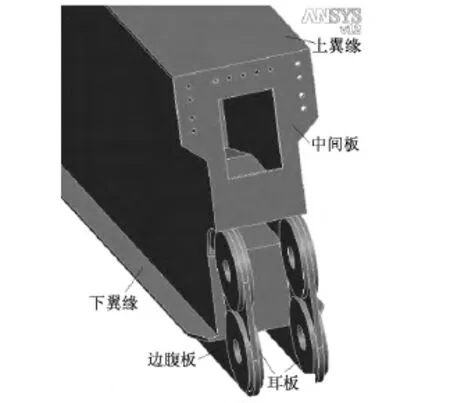
图2 梁段2示意图Fig.2 Schematic diagram of beam section 2
本文根据合作企业实际工程需要,参照国外相关资料及桥梁结构,构造出了一种新型箱形钢梁双销轴拼接节点形式,该拼接节点具体构造为:截面为3 200 mm ×1 500 mm×30 mm×40 mm的钢梁上部通过厚30 mm的封头端板顶紧并采用10.9级M48高强螺栓连接;截面下部通过两根销轴插入梁段交界处的耳板连接,其中梁段1的四块耳板厚度为80 mm,梁段2的两块耳板厚度为160 mm。销轴为上下布置,两根销轴自上而下的直径分别为230 mm、260 mm,销轴间距为900 mm,上销轴中心距梁中心650 mm,销轴材料为40Cr,其他钢板均为Q345。该拼接节点的具体构造如图1、图2所示,钢梁拼接节点区域如图3所示。
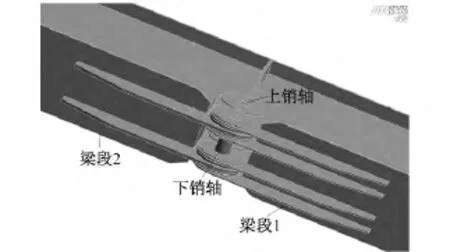
图3 箱形梁拼接节点图Fig.3 Diagram of pin connection of steel-box girders
2 双销轴节点受弯极限承载力理论分析
本文理论分析假设梁截面符合以下假定:梁截面材料受力性能各向同性;材料为理想弹塑性,不考虑应变硬化;变形前后符合平截面假定;不发生局部屈曲。
2.1 销轴连接的极限状态
钢梁在弯矩作用下,拼接节点截面常见的失效现象有:截面下部受拉,达到极限荷载时,耳板销轴孔壁塑性变形常较小,此处易造成突然破坏或脆性破坏;而截面上部受压,由于常设有加劲肋,不易局部失稳,节点破坏前常表现为较大的塑性变形;节点耳板两侧有加强贴板,耳板的净截面破坏和平面外失稳发生概率较小,而孔壁承压破坏和销轴的弯曲剪切破坏易先出现。在以上失效现象中,最易出现的是耳板孔壁塑性变形[8,9]。
基于以上现象,本文采用图4所示销轴孔壁压应力分布模式即孔壁压应力沿孔壁圆弧变化模式,分析节点耳板承载性能。假设半径为R的圆弧上任一点与销轴圆心连线L1和变形后销轴圆心与耳板孔圆心连线L2的夹角为θ,则在该圆弧点上的孔壁压应力为式中,R0为孔壁初始半径;R为变形后孔壁半径;q为孔壁承压极限应力。
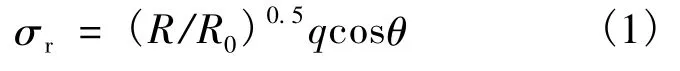
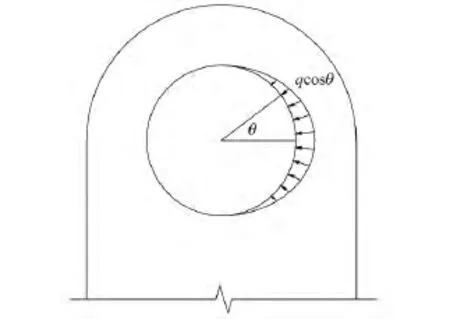
图4 本文孔壁承压应力图Fig.4 Bearing strength stress in this paper
假定R0=R,由此,可得出孔壁承压极限状态时的销轴剪力F为
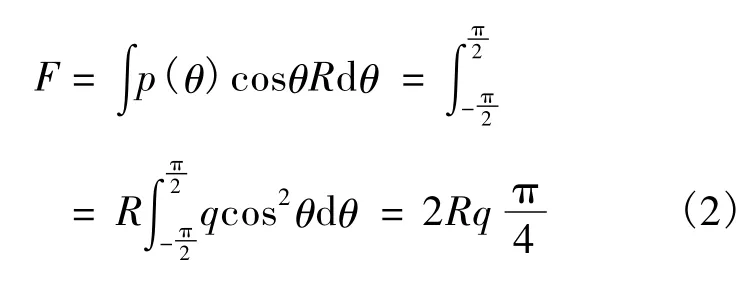
2.2 双销轴应力关系
当拼接节点采用上下双销轴时,上下销轴不会同时进入极限状态。由于梁截面刚度较大,根据平截面假定,若梁受弯后截面转角为θ,则上、下销轴的应变关系为
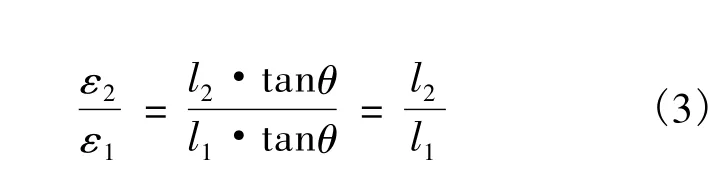
式中,l1和l2分别为下销轴和上销轴到中和轴的距离。
2.3 双销轴节点的极限承载力公式
由于假定钢梁材料为理想弹塑性,所以,截面受压部分达到极限荷载时,可认为截面该部分压应力为均匀分布。对于销轴连接的梁,假定当销轴孔壁进入极限状态时,腹板上部同时达到屈服状态,则销轴拼接节点的梁截面可能出现的极限状态如图5所示,分别对应于中和轴未上移时受压破坏、中和轴上移后销轴破坏、中和轴上移后受压破坏。
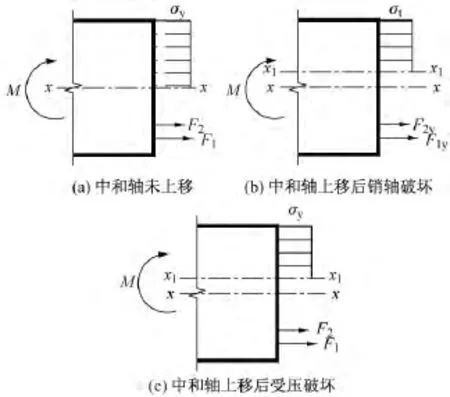
图5 销轴节点极限状态Fig.5 The limit state of pin connection
根据图5所示的简化计算简图,分别考虑轴向力平衡和力矩平衡条件,可得到钢箱梁销轴连接受弯极限承载力的简化计算基本公式为
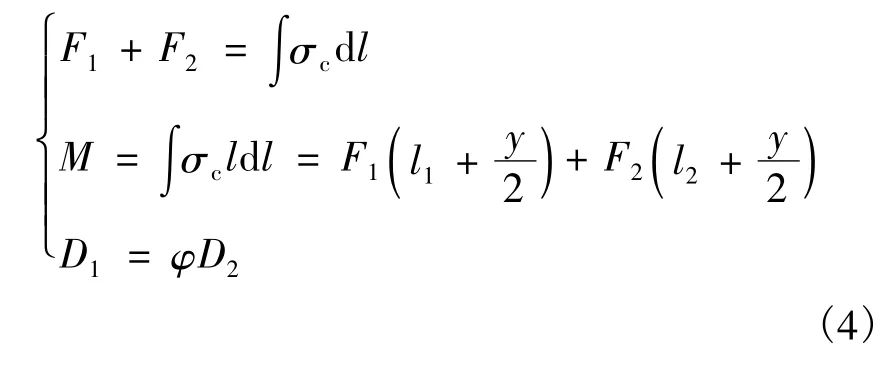
式中,F1和F2分别为下销轴和上销轴的抗剪承载力;l1和l2分别为下、上销轴等效集中荷载到截面中和轴的距离;σc为截面受压区平均压应力;φ为下、上销轴直径比;y为受压区等效集中力作用点距中和轴距离。
设施辣椒栽培,生产周期长,后期生长较旺盛,进行打杈疏果主要是去弱小及密生枝,同时打顶摘心,达到通风的目的,以提高品质、增加产量。
根据式(3),可计算得到本文构造节点的极限弯矩为93 982 kN·m,节点极限状态为销轴孔壁破坏,且截面受压区也部分进入塑性,较充分地利用了材料。
3 双销轴节点受弯极限承载力有限元分析
3.1 节点有限元模型
本文应用ANSYS有限元软件对销轴节点进行有限元数值分析。由于钢箱梁受弯时,上部截面受压,高强螺栓无作用,所以,有限元计算模型忽略高强螺栓。节点钢板材料为Q345钢,屈服强度为 345 MPa,弹性模量为 2.06 ×105MPa,采用理想弹塑性本构关系。
考虑节点的实际受力状态,有限元模型的荷载和约束如图6所示,具体约束条件如表1所示。钢箱梁两端为铰接,荷载为均布荷载(1.2 kN/m)施加于梁上翼缘。
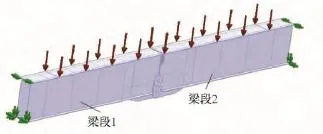
图6 有限元模型的荷载和约束示意图Fig.6 Schematic diagram of load and constraint of finite element model
节点板件采用ANSYS中Solid186单元模拟,耳板与销轴之间的相互作用采用接触单元模拟,其中销轴接触面采用Conta174单元模拟,耳板接触面采用Targe170单元模拟。
3.2 节点有限元数值分析结果
数值分析结果如图7—图9所示。当荷载达16倍设计荷载(1.2 kN/m)时,节点的应力状态如图7所示。梁段1、2截面的受压边缘仍然处于弹性,最大应力接近屈服应力。下销轴节点出现局部应力集中,最大应力达屈服应力,上销轴节点由于受力较小处于弹性,最大应力为240.6 MPa。此时销轴节点部分进入塑性,截面受压翼缘接近屈服。
荷载达19.5倍设计荷载时节点的应力状态如图8所示。此时下销轴节点较大区域屈服,塑性变形增大,截面有微小的转角,使得原先贴合的部分受压区板件脱开,受压区减少,中和轴明显上移。
荷载达22.5倍设计荷载时节点的应力状态如图9所示。上销轴节点有较少部分进入塑性,而下销轴节点大部分进入塑性,截面受压板件也部分进入了塑性,所以,认为销轴节点进入极限状态,即整个拼接节点达到极限受力状态。
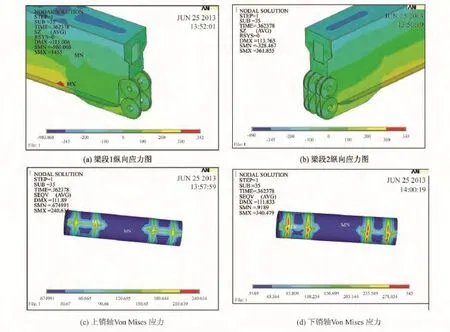
图7 16倍设计荷载时钢箱梁节点各构件应力图Fig.7 Stress figure of each connection component when 16 times design load
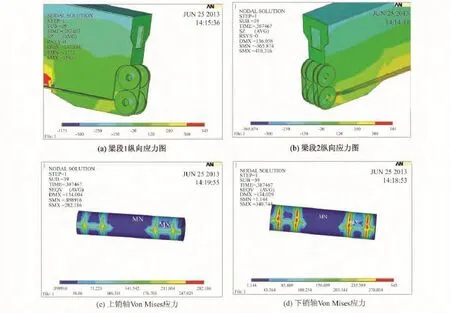
图8 19.5倍设计荷载时钢箱梁节点各构件应力图Fig.8 Stress figure of each connection component when 19.5 times design load
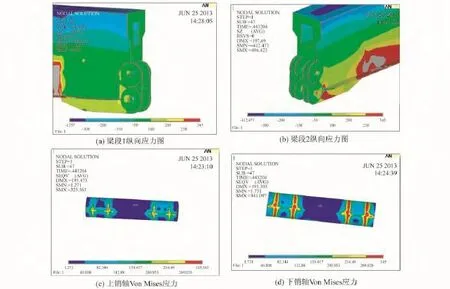
图9 22.5倍设计荷载时钢箱梁节点各构件应力图Fig.9 Stress figure of each connection component when 22.5 times design load
从上述分析结果可看出,该节点在销轴节点整体进入塑性时,截面受压区也部分达到塑性,因此,节点设计安全合理。
有限元数值计算得到的节点极限承载力为22.5倍的设计荷载,而设计荷载下节点处弯矩M0=4 320 kN·m,所以,数值计算得到的节点极限弯矩Mu=95 040 kN·m。通过本文简化计算公式求得的节点极限弯矩Mu=93 982 kN·m。两者之间的误差3.3%,且简化计算公式较为保守。计算结果比较说明,本文简化计算公式较为准确可行。
4 结论
本文根据合作企业需要,参照桥梁及机械结构的连接方式,构造出了用于建筑结构钢梁拼接的双销轴节点,进而提出了双销轴节点极限承载力简化计算公式,通过理论分析和数值计算比较研究,得到的结论如下:
(1)本文构造的双销轴节点,适用于钢梁特别是可拆卸钢梁的拼接。
(2)针对销轴节点,本文提出的双销轴节点承载力简化计算公式正确有效。
(3)采用简化公式计算本文构造的双销轴节点的弯矩极限承载力为93 982 kN·m,通过ANSYS有限元模拟,得到节点的极限承载力为95 040 kN·m,与简化计算误差为3.3%。
[1] 孙从永,郝建鸿,许锋.超大箱形钢梁施工技术的开发和应用[J].钢结构,2007,22(2):85-88.Sun Congyong,Hao Jianhong,Xu Feng.Development and application of construction technique for super box steel girder[J].Steel Construction,2007,22(2):85-88.(in Chinese)
[2] 叶康,李国强,张彬.钢框架半刚性连接研究综述[J].结构工程师,2005,21(8):66-69.Ye Kang,Li Guoqiang,Zhang Bin.Summarizing in research for semi-rigid connections for steel frame structures[J].Structural Engineers,2005,21(8):66-69.(in Chinese)
[3] 张梁,陈以一.方钢管柱与H型钢梁连接形式评述[J].结构工程师,2009,25(8):129-137.Zhang Liang,Chen Yiyi.Overview of connection types between rectangular tubular columns and H-shaped beams[J].Structural Engineers,2009,25(8):129-137.(in Chinese)
[4] 张立君,张俊宝.提高钢结构梁柱焊接节点抗震性能的探讨[J].结构工程师,2003,19(4):43-47.Zhang Lijun,Zhang Junbao.Discussion for the improvement of seismic performance of beam-column welded connection in steel structures[J].Structural Engineers,2003,19(4):43-47.(in Chinese)
[5] 韦艳娜.钢箱梁新型拼接节点承载性能研究[D].上海:同济大学,2011.Wei Yanna.Loading behavior of the split-joint used in steel-box girders[D].Shanghai:Tongji University,2011.(in Chinese)
[6] 罗永赤.钢结构工程中的销铰连接研究综述[J].武汉:长江大学学报,2009,6(3):292-295.Luo Yongchi.Research summary on pin connection in steel structure[J].Wuhan:Journal of Yangtze University,2009,6(3):292-295.(in Chinese)
[7] 常鸿飞,夏军武,孙东明.钢框架带悬臂梁段拼接节点非线性分析[J].结构工程师,2011,27(4):57-62.Chang Hongfei,Xia Junwu,Sun Dongming.Nonlinear analysis on the steel frame joint with cantilever beam splicing[J].Structural Engineers,2011,27(4):57-62.(in Chinese)
[8] 朱浩.大型钢结构节点销轴连接接触力分布研究[D].武汉:武汉理工大学,2011.Zhu Hao.The research of contact force distribution of pin connection for large steel structure joint[D].Wuhan University of Technology,2011.(in Chinese)
[9] 徐晗.铝合金连接节点性能研究[D].上海:同济大学,2012.Xu Han.The loading behavior of aluminum alloy bolted connections and joints[D].Shanghai:Tongji U-niversity,2012.(in Chinese)

