热传导方程的一个三层差分格式

陈国玉，谢英超，程燕

(陆军军官学院a.数学教研室;b.研究生管理大队，合肥230031)

热传导方程的一个三层差分格式

陈国玉a，谢英超b，程燕a

(陆军军官学院a.数学教研室;b.研究生管理大队，合肥230031)

有限差分方法是求解偏微分方程的重要的数值方法之一。利用有限差分方法构造了一个三层差分格式，当θ=1－时截断误差达到了O(τ2+h4)，并将精确解和数值解进行了对比，数值结果显示，该格式是求解热传导方程的高精度格式。

有限差分法;热传导方程;差分格式;截断误差;matlab

本文考虑一维热传导方程的定解问题

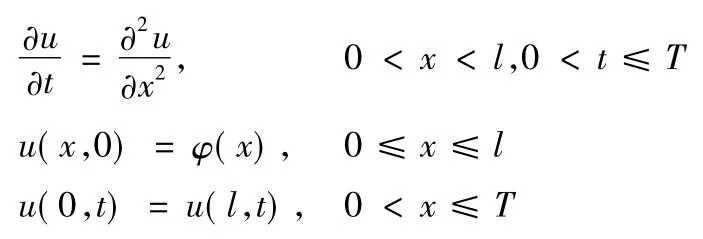
其中:a为常数，φ(x)为连续函数。

目前常用的差分格式有向前Euler格式、向后Euler格式、Crank－Nicolson格式、Richardson格式，这些格式的精度都不高，本文将给出一个新的三层差分格式，精度将达到O(τ2+h4)，并通过数值例子进行验证。

1 差分格式的建立

为了使精度达到O(τ2+h4)，用关于t的向后二步差商近似，即

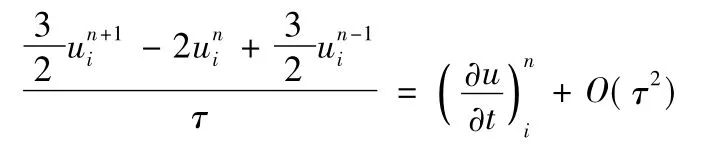
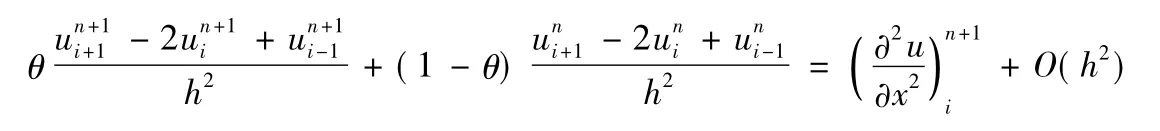
得到下面的差分格式:

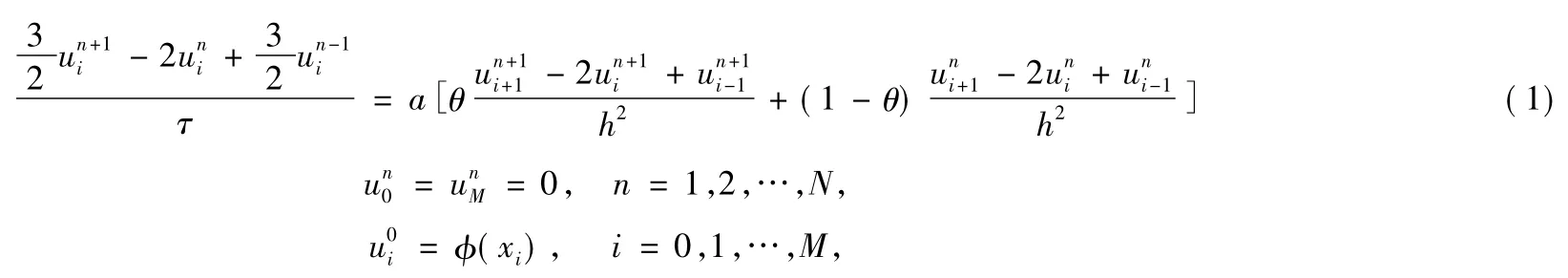
2 格式的截断误差

式(1)的截断误差为

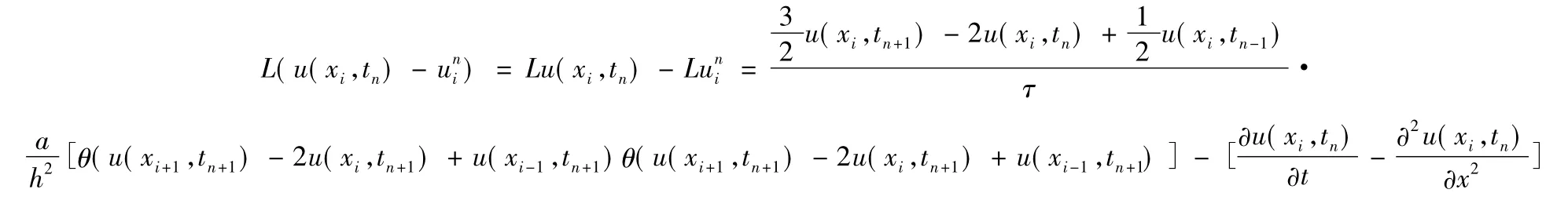
由泰勒公式得

故有

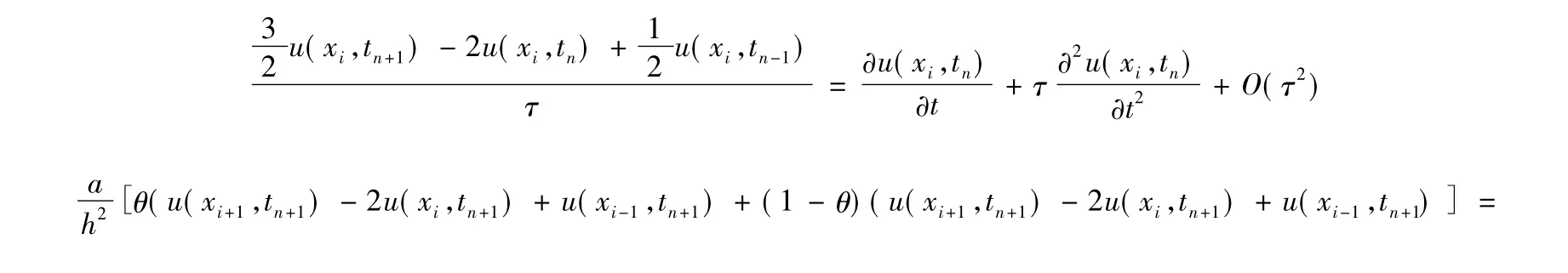
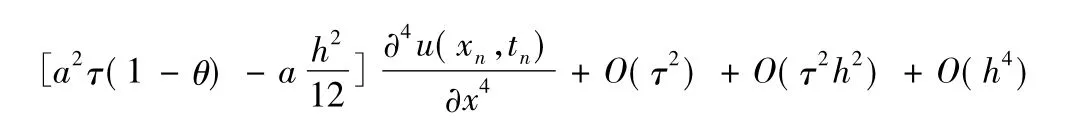
3 差分格式的先验估计式

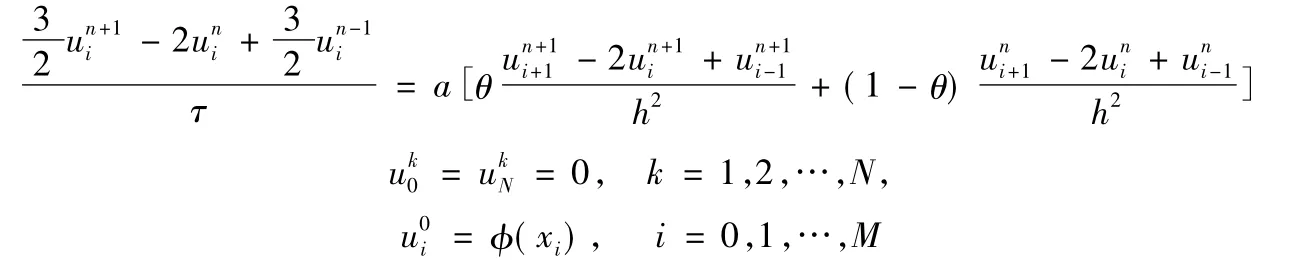
4 数值例子

考虑一维热传导方程的定解问题

编写Matlab程序，给出精确解，数值解及误差的图形(图1为精确解的图形，图2精确解的图形，图3为误差的图形，图4为当θ=1－112r ≈0.1975时的误差图)。

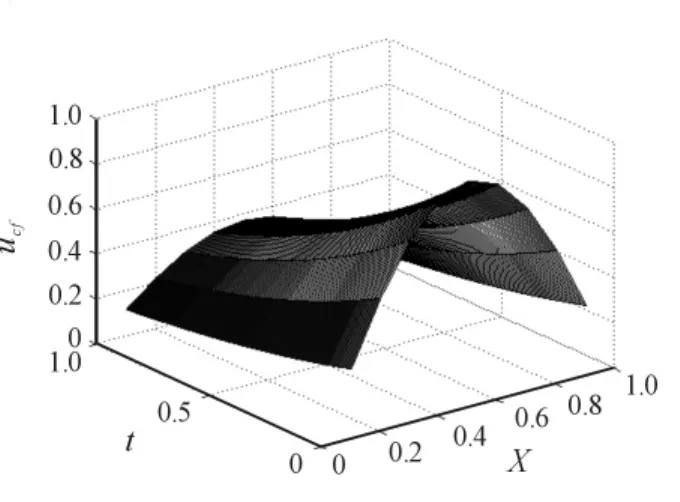
图1 精确解的图形(Ucf)

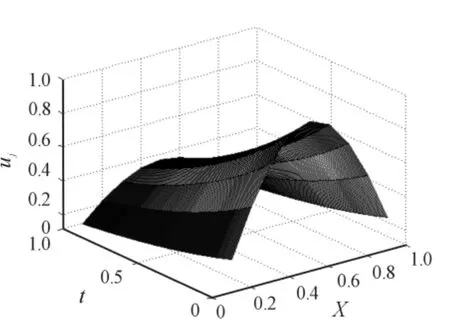
图2 精确解的图形(Uj)

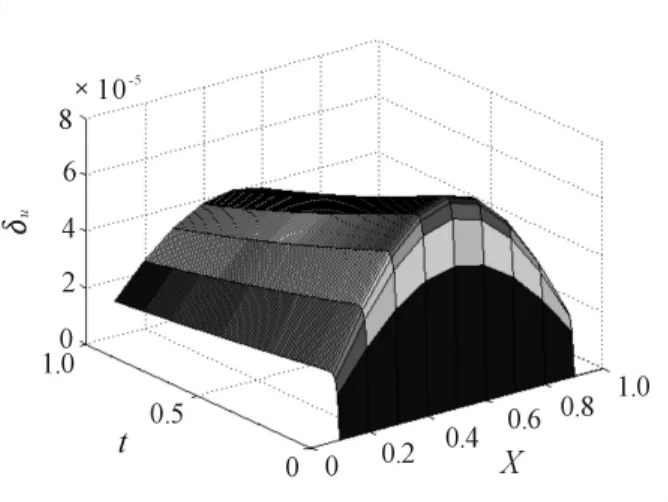
图3 误差的图形

图4 当θ=1－≈0.1975时的误差

差分格式和精确解的绝对误差如表1所示。

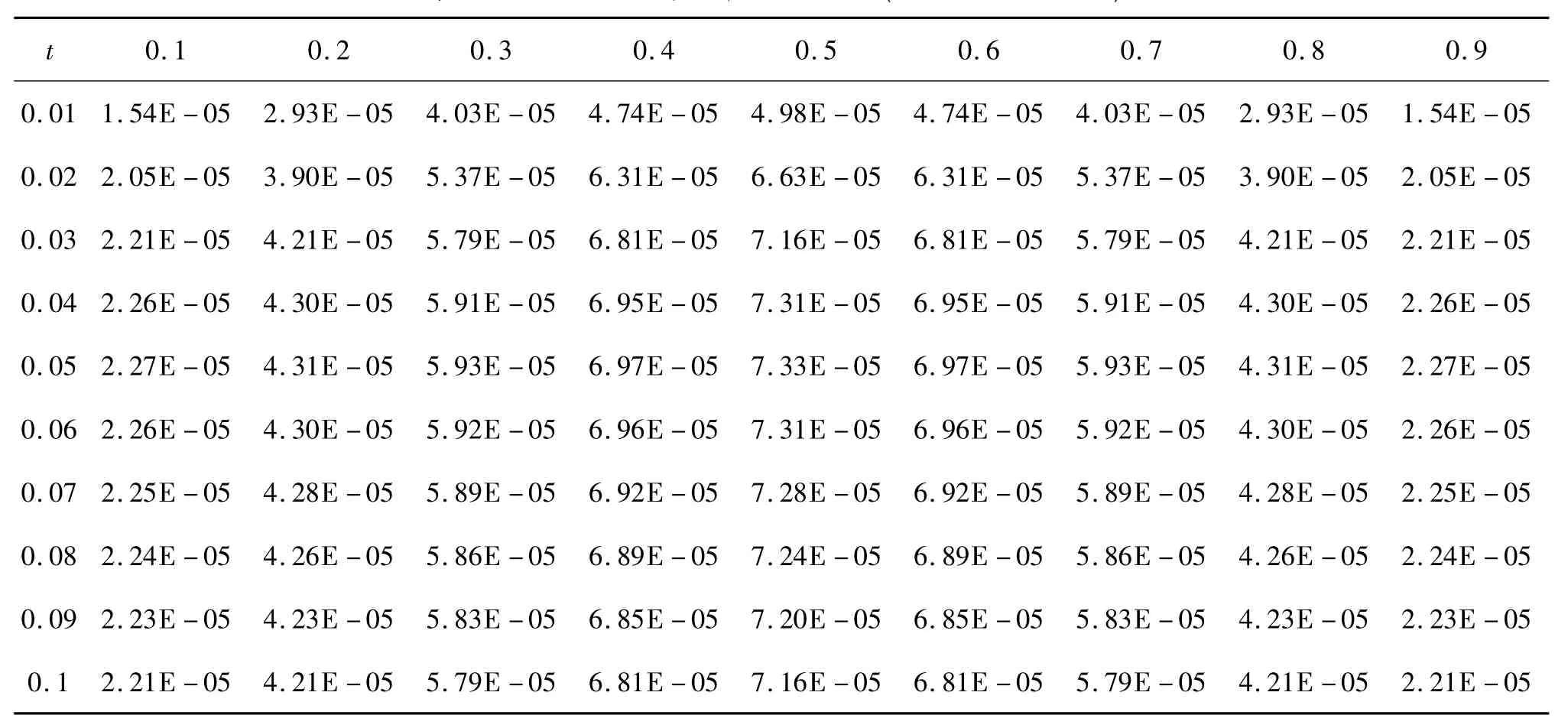
表1 差分格式和精确解的绝对误差(纵向为x横向为t)

由图形及表格可以看出所构造的格式是有效的。

［1］陈国玉.邱国新.拟线性双曲－抛物奇异摄动问题的O(ε3)阶渐近展开［J］.甘肃科学学报，2008(1):20－23.

［2］陈国玉.拟线性双曲－抛物奇异摄动问题的变步长差分格式［J］.甘肃科学学报，2012，24(2):17－19.

［3］郭明普，吕保献.Schrödinger方程的一个新显格［J］.郑州航空工业管理学院学报，2003，21(2):17－18.

［4］孙志忠.偏微分方程数值解法［M］.北京:科学出版社，2005.

［5］戴嘉尊.邱建贤.微分方程数值解法［M］.南京:东南大学出版社，2004.

(责任编辑杨继森)

Three-leval Scheme for Solving Heat Conduction Equation

CHEN Guo－yua，XIE Ying－chaob，CHENG Yana
(a.Department of Basic Courses;b.Graduate Management Unit，Army Officer Academy of PLA，Hefei230031，China)

Finite difference method is one of the numericalmethods for solving partial differential equations.In this paper，a three－level schemewas builtby using themethod.Its truncation error is O(τ2+h4) whenθ=1－.The exact solution and the numerical solution obitained by this schemewere compared.The comparison shows that this scheme provides highly numerical solution for heat conduction equation.

:finite differencemethod;heat condition equations;difference scheme;truncation error;matlab Citation form at:CHEN Guo－yu，XIE Ying－chao，CHENG Yan.Three－leval Scheme for Solving Heat Conduction Equation［J］.Journal of Sichuan Ordnance，2014(7):143－146.

O241.82Key words:A

1006－0707(2014)07－0143－04

本文引用格式:陈国玉，谢英超，程燕.热传导方程的一个三层差分格式［J］.四川兵工学报，2014(7):143－146.

10.11809/scbgxb2014.07.040

2014－03－10

解放军陆军军官学院基金(2013xyjj－023)。

陈国玉(1974—)，女，硕士，讲师，主要从事偏微分方程研究。