基于光度立体法的织物三维数字化研究
李 健, 马泳潮, 马 文
(陕西科技大学 电气与信息工程学院, 陕西 西安 710021)
0 引言
随着多媒体技术的发展,三维重建技术被广泛应用于电影特效、数字城市、三维游戏、人机交互、非物质文化遗产保护等领域,其研究意义与商业价值越来越凸显出来[1-3].
由于计算机视觉理论的逐渐成熟,从图像中获取物体表面的三维信息的算法己经达到了实际应用的阶段.立体视觉技术[4,5]、Shape From X技术、光度立体技术[6-8]等一系列图形算法可以自动的从单幅或多幅真实物体照片中提取出其三维结构的信息,而这些技术实施简便,设备易于获取,核心部件仅需几台数码相机即可.所以,通过应用计算机视觉理论,从真实物体的照片中重建物体的三维结构的技术是目前得到真实物体3D模型的比较廉价的手段[9-12].
织物的三维仿真技术在服装设计、电脑游戏、影视制作等方面的应用前景非常广阔.由于这项研究有着非常实际的应用背景,世界各国的服装研究机构和企业对这一问题的研究开始高度重视.但是因织物本身的物理特性非常复杂,而且容易高度变形,因此要对织物进行逼真的模拟是非常困难的,这也是计算机图像处理领域内极具挑战性的一个课题,因此对织物的三维重建有着非常重要的意义[13,14].
在计算机视觉领域中对于织物的三维重建通常采用基于双目视觉的立体匹配算法,但是立体匹配一直是双目视觉的难点问题,通过这种方法实现重建是一个比较繁琐的过程.为了简单起见,我们在光度立体法的基础上采用同材质的采样球,近似的求解出同样环境下亮度与法向的关系,然后把这种关系运用到被测的织物上来,以求出相对应的三维信息.该方法不仅具有系统成本低廉、原理简单的优点,且三维数字化的效果较好.
1 理论基础与算法设计
1.1 光度立体法
从明暗恢复形状(Shape From Shading,简称SFS)是计算机视觉中三维形状恢复问题的关键技术之一,其任务是利用图像中物体表面的明暗变化来恢复其表面各点的相对高度或表面法向等参数值,为进一步对物体进行三维重构奠定基础.光度立体法就是在传统SFS方法存在病态解的基础上演变过来的.
光度立体法的实现就是在多个光源的分别作用下对物体拍摄一组照片,然后通过这组照片去求解物体表面的法向量,进而求出深度.
在朗伯体表面反射模型下,物体表面一点的亮度只与其表面反射系数和表面法方向有关,而且这个关系是线性的.这就给其向量场的计算带了很大的方便,三幅不同光源的光度立体图像中是可以唯一的决定物体表面向量方向的.设图像一点的亮度为I0,其表面的单位法向量为N0,光源方向为S0,反射率为η.则根据朗伯体表面反射模型有:
I0=ηN0·S0
(1)
由于具有三个不同方向的光源分别照射同一点,所以通过公式(1)可以建立如下方程组.
(2)
将公式(2)写成矩阵形式:
I=ηN·S
(3)


图1 光度立体法
1.2 基于采样球实例驱动下的法向量求解
从公式(3)可见,如果已知η、S以及每点的亮度I就可以求出该点相对应的法向量N.然而很遗憾,对一般物体,我们不能保证η是已知的,并且S的求解也需要一定的开销.为了简单起见,我们采用同材质采样球去近似的求解矩阵M=η*S的值.公式(3)可以改写成:
I=M·N
(4)
所以只需要知道M的值,而不需要分别去求解出η与S的值,这样就大大简化了计算的过程.又因为采样球和目标物体的材质是一样的,所处的环境也是一样的,所以它们表面亮度与法向量对应的关系也是近似一样的,即M是一样的.
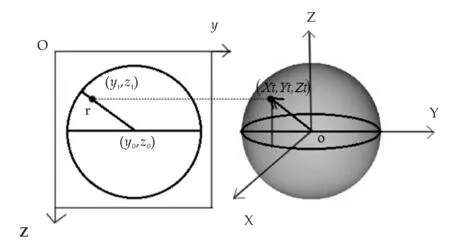
图2 采样球的二维到三维转化
如图2所示,右边为空间坐标系中的采样球,左边为正交投影后采样球在图像平面坐标系中所对应的像,并且图像平面坐标系与空间坐标系中的YOZ平面重合.对于采样球映射到图片上的圆,可以先求出圆心坐标(y0,z0),以及半径r,再通过公式(5)求出圆上任何一点t(yt,zt)所对应的采样球上的点T(Xt,Yt,Zt),由于原点在球心上,坐标值也为该点所在切面的单位法向量.
(5)
球上任一点T都有对应的I向量(I1,I2,I3),因此由公式(4)可得:
(6)
把圆上每个像素点所对应的值带入公式(6)通过最小二乘法求解出矩阵M.然后通过公式(4)就可以直接求出被测物体图片上任何一点的法向量N.这种方法比kd搜索最接近法向量要快的多,而且不会因为被测物体图片像素的增大而影响运算速度.
1.3 从法向量求解深度值
通过上节可以求出被测物体表面上点的切面法向量,再运用法向量就可以求解出物体表面上点的相对深度值.由切平面理论,方向与切平面方向两个主轴垂直,所以对每个像素点的深度都可以列两个约束方程,如图3所示.
图3 像素三角化
如图3所示,对于m×n的图像,每个像素点(x,y)都有其对应的深度值z.物体的表面切向可以用高度值来表示,即:
V1=(x+1,y,zx+1,y)-(x,y,zx,y)
=(1,0,zx+1,y-zx,y)
(7)
物体每一点的法向和表面切向相垂直,则:
N·V1=0
(8)
同理可得:
V1=(x,y+1,zx,y+1)-(x,y,zx,y)
=(0,1,zx,y+1-zx,y)
(9)
N·V1=0
(10)
展开,得:
nx+nz(zx+1,y-zx,y)=0
(11)
由此,对于m×n个像素的图像,可以获得2×m×n个如上的约束.每点的N是已知的,z是标量.所有像素点的约束组成了一组方程,用矩阵表示的话,则可以得到稀疏矩阵A,A为2m×n.通过求解矩阵方程就可以得到被测物体投影到图片上点的相对深度值z,它的大小是以图像平面两像素点的距离为单位长度的.从而确定了物体表面相对的三维坐标(x,y,z).
1.4 算法设计
在以上的理论基础上,我们设计的算法如下所示.
输入:采样球与被测物体在三个不同方向光照射下各采集到的三张同样大小的jpg格式照片.这些照片中被测物体位置始终不变,被测物体是在黑色背景前拍摄的,便于有效区域分离.
输出:被测物体的三维点云数据.
过程如下:
(1)对图片做预处理,使图片变成灰度图像,根据灰度阈值(I1>20或I2>20或I3>20)区分有效区域和背景区域,对于处于背景区域的点的灰度值设置成(I1=0,I2=0,I3=0).
(2)对采样球图片运用公式(5)与(6)求解出矩阵M.
(3)对被测物体图片上的每一有效点通过公式(4)求解出对应的法向量N.
(4)通过公式(7)~(11)求解出每一点所对应的深度值,即可以得到这些点的相对三维坐标.
2 实验设计与结果分析
2.1 实验方案
实验的算法设计如1.4所示.直接输入在实验环境中所采集到的图片,就可以求解出被测物体表面上点的三维坐标,即实现了对被测物体表面的三维数字化.如何搭建实验环境以采集到较好的图片是我们研究的另一个重要内容.
为了快速得到理想的实验环境,我们采用“虚实结合”的方法.“虚”是指在仿真软件中操作实验,目的是为了避免由于前期经验不足造成实验器材的浪费,并且可以大大提高实验速度.“实”是指在一定经验参数的指导下搭建真实的实验环境,把理论付之实践,对于现实中存在的问题再进行修改.
通过反复实验,我们最终确定的实验环境如图4所示.

图4 实验环境
搭建实验环境注意以下几点:
(1)三个平行光源与物体之间形成一个正三棱锥型,物体所在位置为顶点,三个面光源都朝向被测物体,照相机放在中轴线上,距被测物体远一些,用黑布作为背景.
(2)三光源与中心轴的角度保持在20 °~40 °之间,光源距被测物体的距离越远越好,但是要保证有足够的光线照到物体上.
(3)照相机用中长焦、小光圈、慢快门,保证在不曝光的前提下使图像尽量亮一点.
(4)标定球和被测物体具有相同的材质,先对标定球进行拍照,然后移开标定球,把被测物放在标定球的位置进行拍照.
通过上面的实验可以得到标定球和被测物体在三种不同光照下的图片,把这些图片输入到1.4所示的算法里就可以得到被测物体的三维信息.
2.2 仿真实验设计与结果分析
仿真实验是在3DS max 软件平台上搭建的,并配备最流行的光路计算插件vray渲染器,这样可以计算出比较真实的光线效果.在实验中,为了得到平行光源,三盏灯均使用vray自带的vray平面光源. 模拟环境下实验的过程和结果如图5所示,第一列为原物,把原物和采样球放在实验环境中分时开启不同方向的光源就可以采集到六幅图片(如图5第二列所示).把这六幅图片输入到1.4的算法中就可以得到如图5第三列的重建效果.

图5 仿真实验结果
从结果看,建模的效果非常理想.不足之处就是对于遮挡部分同样没法重建出三维结构.
2.3 真实实验设计与结果分析
真实实验环境下,为了使点光源接近于互不干扰的平行光源,我们采用如图6所示的灯头装置.为了满足被测物体与采样球材质一样,我们把和被测物体相同的材质直接包裹在一个球体模型上,如图6所示.

图6 光源与采样球
实验结果如图7所示:

图7 真实环境实验结果
从实验结果看,重建的三维结构与真实结构较为接近,但是没有仿真环境下的效果好.主要是因为仿真环境下物体与采样球都是标准的朗伯体,这在真实环境下难以实现.从图7可以看到下一行中物体的垂直效果要比上一行的好一些,这跟被测物体与环境的相对大小有关.如果环境大小一定的话,被测物体越小,物体表面到光源的距离对物体表面亮度的影响就越小,重建出的效果自然也就越好.所以该实验适合在比较大的空间中操作,将光源放置在距物体比较远的位置.
3 结论
本文通过采样球去近似的求解被测物体在相同环境下亮度与法向的关系,然后把这种关系运用到被测物体上以求出相对应的法向.这样就可以避开求解光源方向、反射率以及立体匹配等一些比较麻烦的步骤,并且可以取得令人满意的重建效果.
本文考虑的是在织物不动的情况下进行的三维重建,如果织物发生形变,这种方法就不太适合.然而动态变化的织物才具有更大的价值和研究意义,所以接下来的任务就是要结合其他三维重建的方法,寻找出一种能够重建出动态织物三维结构的方法.
[1]王宇宙.计算机视觉三维重建理论与应用[D].西安:西北大学,2004.
[2]张广军.机器视觉[M].北京:科学出版社,2005:3-10.
[3]蔡钦涛.基于图像的三维重建技术研究[D].杭州:浙江大学,2004.
[4]杨 明.基于双目立体视觉的三维重建研究[D].武汉:武汉工程大学,2012.
[5]钱曾波,邱振戈,张永强.计算机立体视觉研究的进展[J].测绘学院学报,2001,18(4):267-272.
[6]Daniel Vlasic,Pieter Peers, I Iya Baran,et al.Dynamic shape capture using multi-view photomeric stereo[J].ACM Transactions on Graphics (TOG),2009,28(5):174.
[7]张屹凌.基于光度立体算法的图像建模系统的设计及实现[D].杭州:浙江大学,2006.
[8]李德仁,王新华,黄培之.基于光度立体的物体三维表面重建[J].测绘学报,1995,24(3):197-203.
[9]佟 帅,徐晓刚,易成涛,等.基于视觉的三维重建技术综述[J].计算机应用研究,2011(7):2 411-2 417.
[10]陈 坤.多视图三维立体重建方法[D].杭州:浙江大学,2013.
[11]冯树彪.基于图像的三维重建[D].苏州:江南大学,2012.
[12]林慕清.基于光度立体法的三维重建技术的研究与实现[D].沈阳:东北大学,2010.
[13]倪晓庆.织物的三维动态仿真研究[D].杭州:浙江理工大学,2012.
[14]贾 玥.三维布料动态仿真[D].大连:辽宁师范大学,2013.

