纸张匀度模型的分析与评价

李 健， 徐建荣，2 , 俞宏明, 徐永建

(1.陕西科技大学 电气与信息工程学院， 陕西 西安 710021； 2.陕西科技大学 职业教育师范学院， 陕西 西安 710021； 3.广东冠豪高新技术有限公司， 广东 湛江 524022； 4.陕西科技大学 轻工与能源学院, 陕西 西安 710021)

0 引言

纸张的匀度是纸张在三维方向上的质量分布，表示其结构的均一性.通常是用来描述纸张中纤维及其他固体物质(如填料等)分布相对均匀程度的情况，即在一定面积上纤维和结构组成的分布情况[1].造成纸张不均匀性的实质有两点：纸张从一点到另一点的质量或者定量的变化以及纸张单位面积密度的变化.纸张匀度质量是其取得优美外观和良好强度的必要条件，是评价纸张结构和性能的重要指标之一.纸张匀度几乎影响了纸张所有物理和光学性能，是提高纸张印刷适性、浸渍和涂布适应性、机械强度的重要因素[2].在造纸行业中，以较少的原料生产出较高质量的产品，控制匀度的检测是关键.

匀度的检测一般是在均匀的光线照射下，用眼睛观测纸张的透光情况，需要和一定匀度的标准纸样进行对比来判断匀度的好坏，或者依靠观察者的经验来判断[2,3].这种评价方法是非常主观的，在很大程度上取决于观测者的技术和经验，因此误差大.现有的检测方法主要是根据Kubelka-Munk理论，通过测量纸张对光线或β射线的吸收程度来测量纸张的局部定量，计算求出纸张的匀度指数.匀度测量仪器分为三大类：β-射线透射式、β-射线照相法和光透射式[1].仪器测量纸张匀度精度高，但价格昂贵，尚未普及.利用计算机图像分析技术的纸张匀度表征，由于其思路简洁，实现方便，在纸张匀度表征方法中，已经得到国内外研究者的认可[4].其核心思想是采用数学的方法分析数字图像，避免了对经验丰富观察者的需要以及人眼主观评价误差等缺点.但是，由于“纸张匀度”这一物理量本身的特殊性，到目前为止，尚未找到一种公认的表征算法.基于上述原因，本文对三种基于计算机图像处理技术得到的纸张匀度模型(标准匀度指数表征[5]、梯度法表征[6]以及Jordan比周长法表征[7,8])进行分析与评价，对比三种模型的优缺点，从而为造纸企业在分析纸张匀度时提供理论指导.

1 不同匀度模型的理论分析

在过去几年里，国内外研究者已经利用计算机视觉系统及图像处理技术[9-15]进行了纸张匀度分析，构建了多种纸张匀度分析系统，下面我们就标准匀度指数、梯度法以及Jordan比周长算法表征纸张匀度进行理论分析与评价.

1.1 标准匀度指数表征

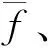
(1)

(2)

(3)

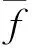
同均方差的纸张，用肉眼观测时却发现纸张的匀度不同，发现平均定量小的纸张匀度较差，平均定量大的纸张匀度较好.统计学中，如果度量单位与平均数相同，则直接利用标准差来比较；但是如果衡量单位和/或平均数不同时，就不能采用标准差，而需要采用标准差与平均数的比值来比较，即变异系数.这种匀度的表征方法，既考虑了纸张平均定量对匀度的影响，又考虑了局部定量的偏离程度，较为全面的反映了纸张的匀度信息.该匀度表征方法计算简单，运算速度较快，能够在一定程度上表征纸张的匀度指数，反映纸张的匀度信息，但是，文献记载[6]，对于纹理不同的两幅图像，表征匀度指数相同，但是匀度却有明显差别，见图1所示.

图1 数字特征相同的两幅纹理图

1.2 梯度法表征

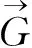
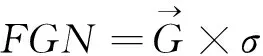
(4)

(5)

(6)

(7)

G[f(x,y)]=

(8)

G[f(x,y)]=

(9)

从上面的分析可知，梯度指数既反映了纸张局部定量的微弱变化，又反映了整体定量的变化情况，较全面的反映了纸张的匀度信息，是一种理想的匀度计算模型.但是在纸张匀度在线检测时，由于机械震动等干扰因素，导致CCD采集的图像中存在噪声，该算法在处理过程中增大了噪音对图像灰度变化的幅度，从而对计算结果的准确度有一定的影响.

1.3 Jordan比周长表征

根据纸页的三维结构以及光透射法分析可以得到纤维絮聚团在二维空间中的投影信息，有研究者对这些投影信息进行处理，可以间接反映纸张定量分布，从而提出了Jordan比周长纸张匀度的表征，这种模型是对纸张三维结构运用二阶统计学的方法得到的.它将纸页中的纤维絮团看作是局部定量比纸样平均定量高的区域.在二维投影中，絮聚团轮廓面积越小，纸张的匀度越好.为了有效提取纤维絮聚团的轮廓信息，需要对图像进行滤波和二值化处理，使图像变得简单，数据量减少，凸显出感兴趣的目标轮廓，但是在进行二值化处理和分析之前，需要先将其转化为灰度图像，在图像进行二值化处理时，处理的阈值应为平均定量对应的灰度值，为了分析图像方便，取图像灰度级的50%作为阈值，得到纤维絮聚团的特征轮廓线，如图2所示.将这些轮廓线的边界长度迭加后除以采样区域的面积，就得到了Jordan比周长匀度指数，见公式(10)所示[4].

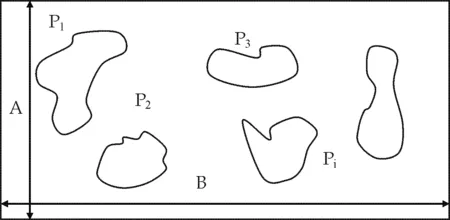
图2 纸张纤维絮聚团轮廓图

(10)

其中，N为所得轮廓边界总数；Pi为第i个纤维絮聚团的轮廓线的边界长度；B和A分别为采样区域的长和宽；SP为Jordan比周长匀度指数.

Jordan比周长算法在进行匀度表征时，对纤维的絮聚团的不均匀性特别敏感，可是采用数字图像分析时，因为没有足够的灰度级分辨率将纸张絮聚团的轮廓特征区分出来，常采用高斯插值法在一个灰度级内增加灰度级数，可这样又会给算法带来复杂性.

2 三种匀度模型计算结果评价

本次实验采用自制纸张作为分析纸样，来评价上述三种匀度模型.取等量的纸浆数份(选取APMP浆)，以不同的搅拌次数在疏解机中分别搅拌，抄造匀度不同的纸张，定量为60 g/m2.在相同的条件下对这些纸样进行图像采集，其灰度图像如图3～图6所示.采用上述三种匀度指数模型分别计算各样张的匀度，在数字图像处理过程中采用均一化处理匀度图像，同时，选定18个对纸张匀度检测有经验的人员进行视觉评价，最终将数字图像处理的结果与视觉评价结果相对比，结果如表1所示.

表1 三种匀度模型及视觉评级的匀度指数

图 5 C试样的 图 6 D试样的 灰度图像 灰度图像

从图3～图6及表1结果可以看出，标准匀度指数、梯度法(典型差分法和Roberts算子)均与人眼视觉评价体系有很好的相关性，其中Rorberts算子求取的平均梯度比典型差分算子求取的平均梯度要大，说明该算法对纸张局部定量变化率越敏感，因此采用Rorberts算子处理纸张得到的匀度效果好，然而Jordan比周长算法计算得到的纸样B、C的值小于纸样A的值，与视觉评价的结果有差异，这主要是因为Jordan比周长算法在进行数字图像处理时没有足够的灰度级分辨率区分纤维絮聚团的轮廓特征，影响了结果的准确度.

3 结论

通过分析由标准匀度指数、梯度法以及Jordan比周长算法构建的纸张匀度指数模型的性能及优缺点，结合三种模型处理的纸样结果与视觉评价结果对比分析可知，标准匀度指数和梯度法计算结果均与人眼视觉评价结果相一致，Roberts算子比典型差分法的计算结果精度高，而Jordan比周

长算法的计算结果与人眼视觉评价结果有差异，需要采用插值法增加灰度等级，提高处理结果的精度，但算法比较复杂，有待进一步研究.

[1] 卢谦和.造纸原理与工程[M].北京:中国轻工业出版社,2008：398-400.

[2] 张立九,陈延庆.纸张匀度测试的理论与方法[J].上海造纸,1984(Z1):52-64,68.

[3] 张立九.测试纸张匀度的实用仪器方法[J].上海造纸，1987(Z1):204-210.

[4] 邱书波.基于图像分析技术的纸浆纤维与纸张质量检测方法研究[D].天津：天津大学,2006.

[5] 阎东波,刘焕彬.纸页匀度的一种表征方法[J].中国造纸，1997,16(6):6-11.

[6] 季鸿雁，王永秀，范秋华.一种计算机视觉纸张匀度检测方法[J].青岛大学学报,2003,18(1):35-39.

[7] B D Jordan,N G Nguyen.Specific perimeter:a graininess parameter for formation of print mottle textures[J].Pappuu,1986,6(7):476-482.

[8] B.D Jordan,N G Nguyen.Specific perimeter:a statistic for assessing, formation and print quality by image analysis[J].Tappi Journal,1998,81(10):191-196.

[9] 倪 洁.基于机器视觉的纸病图像处理算法研究与应用[D].南京：南京林业大学,2010.

[10] 周露露.基于机器视觉的纸张缺陷检测算法的研究[D].济南：山东轻工业学院,2012.

[11] 施 祥,胡开堂.基于MATLAB软件的纸张匀度分析方法[J].轻工机械，2010,28(3):82-85.

[12] 陈韦华，胡开堂.利用计算机视觉系统对纸页匀度的研究[J].国际造纸，2000,19(3):48-50.

[13] 常发亮,王 平,乔谊正,等.基于机器视觉的纸张匀度金字塔结构分析方法[J].山东大学学报，2004,34(2):67-70.

[14] 谭尚辉,曾林清，陈巧媚.借助数码摄像技术实现匀度量化分析[J].造纸科学与技术，2007,26(4):62-64.

[15] 姚 敏.数字图像处理[M].北京：机械工业出版社,2006:7-87.

[16] 孙静娟.统计学[M].北京：清华大学出版社,2006:64-90.