基于M-Copula-GJRSK-M模型的沪深两市的相依性分析*

申建平，孙菲，黄敏

(重庆大学数学与统计学院，重庆401331)

基于M-Copula-GJRSK-M模型的沪深两市的相依性分析*

申建平，孙菲，黄敏

(重庆大学数学与统计学院，重庆401331)

金融资产不但存在方差风险，还存在时变偏度风险和时变峰度风险，这使得仅从金融资产的前两阶矩出发来研究风险变化显得十分局限。GJRSK-M模型是描述金融资产的高阶矩风险的有效工具，可对单个金融资产的分布进行拟合，而M-Copula函数能连接组合金融资产的边缘分布，因此本文建立了M-Copula-GJRSK-M模型来研究沪深两股票市场的相依性。实证表明，上证综指和深圳成指对数收益率存在高阶矩风险和风险的非对称性，即指数下跌时，条件方差风险和条件高阶矩风险会增大，且在极端情况下，两市上涨的概率要大于下跌的概率。

M-Copula函数;GJRSK-M模型;高阶矩风险

一、引言

Samuelson［1］在1970年指出:不但可能而且应该在更高阶矩意义下去探讨组合投资及风险规避问题。Lim(1989)［2］讨论三阶矩资产的定价问题;Jondeau(2003)［3］利用基于非中心t分布提出了广义自回归条件偏度、峰度模型(GARCHSK); Davies等(2004)［4］利用多项式目标规划的方法确定均值-方差-偏度-峰度有效前沿;Leon (2005)［5］等给出了基于正态密度的Gram-Charlier展开的GARCHSK模型;2006、2007［6，7］年许启发和张世英给出了一元GARCHSK模型的整套建模方法，提出了一个新的高阶矩波动模型——NAGARCHSK-M，并用此模型度量了高阶矩风险的动态特征、考察了时变高阶矩风险对金融投资决策的影响;蒋翠侠(2007)［8］利用高阶矩风险测度给出了高阶矩风险的动态组合投资策略;张世英和蒋翠侠(2008)［9］将Copula函数和GARCHSK模型相结合解决了高阶矩建模中出现的“维数灾难”问题;王鹏等(2009)［10］提出了一种新的自回归条件异方差-偏度-峰度模型(GJRSK-M)模型，并验证了它的预测能力优于其他高阶矩模型。而以上文献多数文献仅对单一金融资产建模，并对单一资产的高阶矩风险进行评估预测，没有涉及资产间的相关性风险问题;虽有少量的文献对金融资产的多维高阶矩建模，但是没有能够克服由此带来的“维数灾难”问题，而采用Copula技术能够将不同类型分布的边缘连接成一个新的多元分布，并且能够将多元分布的建模分解成边缘分布的建模和相关结构建模两部分，从而解决上述问题;又因部分文献中Copula-NAGARCHSK-M模型体系的NAGARCHSK-M模型不能很直观、明确地对经济含义进行解释，而GJRSK-M模型能很好克服这一毛病，并且GJRSK-M可以很方便地将一些可能的波动解释变量纳入分析框架内。因此，本文选用GJRSK-M模型刻画资产组合的边缘分布，以反映单个资产价格波动的高阶矩风险的时变性和非对称性，再结合混合Copula函数建立M-Copula-GJRSK-M模型来研究组合资产的相依结构并展开实证研究。实证表明，该建模方法效果良好，能有效地解决组合资产的相依性问题。

二、Copula函数的相关理论知识

Sklar定理［11］:令H(，)为具有边缘分布函数F(．)和G(．)的联合边缘分布函数，那么存在一个Copula函数C(·，·)，满足:

H(x，y)=C(F(x)，G(y))(1)

若F(．)和G(．)连续，则C(·，·)唯一确定;反之，若F(．)和G(．)为一元分布函数，C(·，·)为相应的Copula函数，那么由式(1)定义的函数H(·，·)是具有边缘分布F(．)和G(．)的联合分布函数。Gunble Copula函数［12］的分布函数和密度函数分别为:

Gumble Copula函数的密度函数具有非对称性，其密度分布呈“J”字形，即上尾高下尾低。分布函数对分布变量在分布上尾部的变化十分敏感，能够快速地捕捉到上尾相关的变化，但难以捕捉到下尾的相关的变化。Clayton Copula函数［12］的分布函数和密度函数分布为:

Clayton Copula的密度函数具有非对称性，其分布呈“L”字形，即上尾低下尾高。故函数对变量在分布下尾的变化十分敏感，能够快速捕捉到下尾相关的变化，但却对上尾的变化不敏感。Frank Copula函数［12］的分布函数和密度函数分布为:

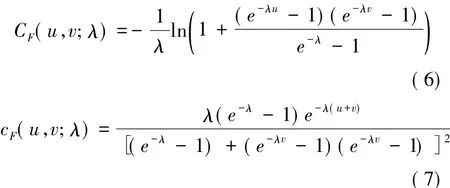
其中λ为相关系数，λ≠0。λ＞0表示随机变量u与v正相关，λ→0表示随机变量趋向于独立，λ＜0表示随机变量u与v负相关。Frank Copula的密度分布呈“U”字形，具有对称性，因此无法捕捉到随机变量间非对称的相关关系。

以上三种阿基米德Copula函数，涵盖了相关结构变化的各种情况，但由于金融市场之间的相关关系是变化的，不会拘泥于某种特定的模式，因此很难用一个简单的Copula函数，如Gumble、Clayton和Frank Copula函数来全面地刻画金融市场之间的相关模式。因此本文选用三者的线性组合来构造混合Copula函数，记作M-Copula函数［12］，其表达式为

其中wG、wCl、wF均大于等于0，wG+wCl+wF= 1;MC3表示由三个Copula函数的线性组合组成的混合Copula函数，CG、CCl和CF分别表示Gumble、Clayton和Frank Copula函数，wG、wCl和wF为相应的Copula函数的权重系数。

三、GJRSK-M模型

王鹏(2009)［10］等人提出了一个新的自回归条件方差模型GJRSK-M模型，并通过样本外预测方法研究表明此模型比现有的高阶矩波动模型有更强的预测能力。模型的形式如下:

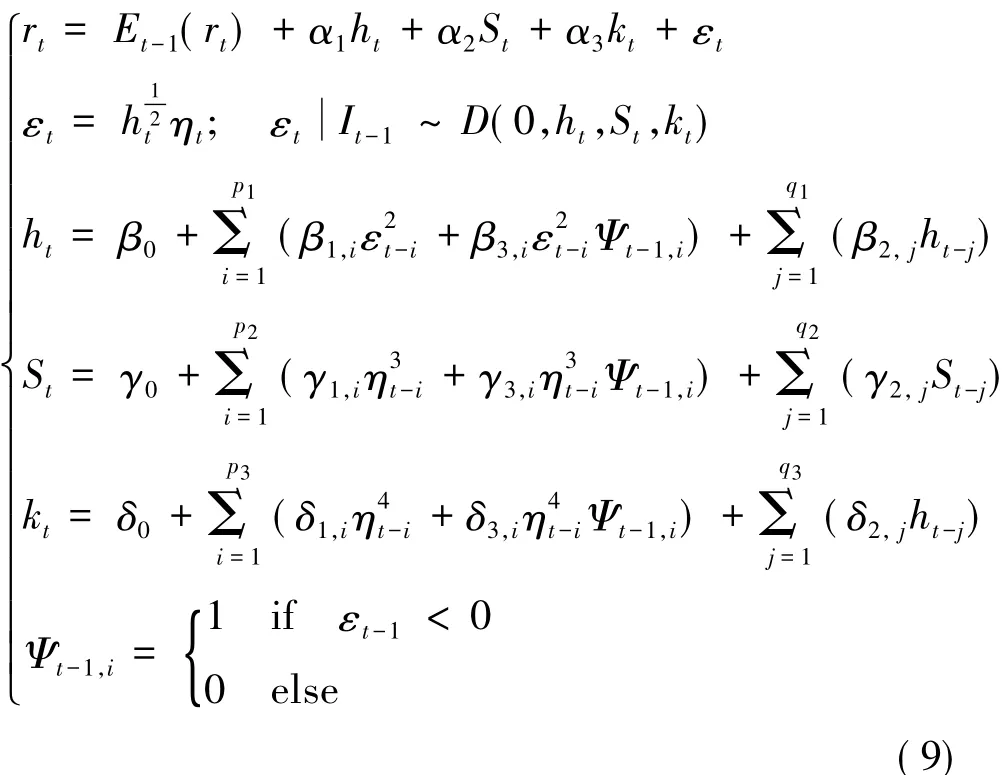
式(9)中Et－1(rt)为基于t－1时刻的条件期望收益;D(0，ht，St，kt)为包含均值、方差、偏度、峰度的任一分布;{ηt}为经过条件标准差调整的残差序列，它是一个独立同分布(i．i．d)的随机变量序列;It－1为t－1时刻的信息集;α1、α2、α3分别为条件方差方程、条件偏度方程、条件峰度方程中的杠杆效应系数;Ψt－1，i为引入的哑变量;p1、q1、p2、q2、p3、q3分别为滞后的阶。在(9)式中，GJRSK-M模型中四个方程都为线性形式，而条件方差、条件偏度和条件峰度的杠杆效应是通过各自的方程中增加符号哑变量进行刻画的，并且在各个方程中以线性形式增加其他可能的解释变量，使得其能更加全面地考察收益率高阶矩序列的时变特征。

四、M-Copula-GJRSK-M模型的建立

为了捕捉资产价格或收益的高阶矩风险以及波动的非对称性，许启发(2006)［6］在GARCH-M模型的基础上，建立了NAGARCHSK-M模型。王鹏等(2009)［10］提出了自回归条件异方差-偏度-峰度模型(GJRSK-M)，并研究了中国股市的条件方差、条件偏度和条件峰度的波动效应持续性和杠杆效应。当方差和峰度增加时，收益波动和极端值出现的概率增大，投资者应该为承担的这部分风险而要求获得更高的利益，因此应该有α1≥0和α3≥0;而在其他条件不变的情况下，投资者喜欢收益偏度为正的投资组合，而讨厌收益偏度为负的投资组合，因此应该有α2≤0。对于方差的杠杆效应，我们用β3，i来刻画，若β3，i＞0，则存在方差杠杆效应。由于金融出现负收益的频率和幅度常常大于正收益，会使收益负偏度的绝对值增大，这一偏度杠杆效应，可以用γ3，i来刻画，若这一效应存在，则γ3，i＞0。绝对值较大的负收益经常出现，会使得收益极值出现的概率大于正态分布下极端值出现的概率，使得收益分布的峰度增加，即为峰度杠杆效应。故本文研究资产组合之间相依结构特征时，利用GJRSK-M模型刻画组合资产的边缘分布，以反映单个资产价格波动的高阶矩风险的时变性和非对称性，再结合M-Copula函数理论建立M-Copula-GJRSK-M模型对动态高阶矩风险进行计量，讨论高阶矩之间的相互关系。以下为N个资产的M-Copula-GJRSK-M模型表达:

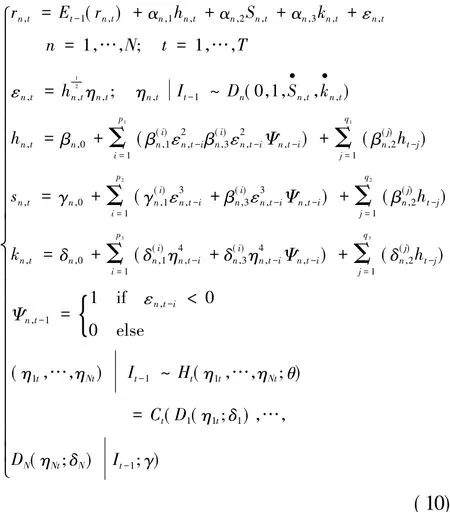
式(10)中对各个资产的边缘分布的建模采用了(9)式，用M-Copula函数将各个边缘分布进行连接，得到(10)式。其中Et－1(rt)为t－1直到时刻的信息集It－1上条件期望价格或收益，是金融资产不受风险影响的基本回报，αn，1、αn，2和αn，3分别为各资产的方差、偏度和峰度的风险溢价;Dn(0，1，sn，t，kn，t)是第n个边缘分布的任意分布，因此可和的分布对应的偏度和峰度分别为各资产方差方程、偏度方程和峰度方程中的杠杆效应参数，p1、q1、p2、q2、p3、q3分别为滞后的阶数。

模型由五组方程组成:均值方程、方差方程、偏度方程、峰度方程和相依结构方程，在波动方程中引入度量各资产价格波动过程中出现的杠杆效应;在均值方程中引入高阶矩的风险项之后，能够衡量各资产单位风险变化对资产价格和收益的影响;通过M-Copula函数来捕捉各资产间的相依结构，因为所以rn，t是ηn，t的单调增函数，根据Copula函数理论，(η1，t，…，ηN，t)和(r1，t，…，rN，t)有相同的Copula函数C。因此(η1，t，…，ηN，t)的相依结构即是(r1，t，…，rN，t)的相依结构。

(一)模型参数估计

模型(10)的参数估计分为两部分，第一部分为对GJRSK-M模型的估计，本文应用文献［10］的方法，即运用正态分布的Gram-Charlier展开并在四阶矩处截断，可以获得:

其中，φ(·)为标准正态分布的密度函数，θ(·)为(11)式中的多项式部分。对残差分布的偏度和峰度的估计等价于对上式条件密度函数的两个参数的估计。但是，由于多项式中的φ(·)可能取值为负，导致会取得负值;另外，g(·)在定义域上的积分可能不等于1，因此Leon对的定义式做了一定的修正，得到条件密度函数:

(二)模型检验

对M-Copula函数对模型拟合度的检验，参考Hu(2002)［13］提出的利用一个服从χ2分布的M经验统计量来评价Copula函数的拟合度，具体实施步骤如下:令{ui}和{vi}(i=1，…，T)都服从i．i．d．(0，1)均匀分布序列，它们是根据估计得到的边缘分布，对观测序列{xi}和{vi}进行概率积分变换之后得到。构造一个包含k×k个单元格的表格G，表格中处于第i行、第j列的单元格记作G(i，j)，表示一个下界为［(i－1)/k，(j－1)/k］、上界为(i/k，j/k)的概率组合，其中k的选取根据样本总体和观测点的总数来确定，既保证有足够多的单元格用于模型拟合度的评价，又要保证每个单元格中有足够多的观测点。对于任何一点(ui，vi)，若(i－1)/k≤ui＜i/k且(j－1)/k≤vi＜j/k，则点(ui，vi)∈G(i，j);若用Ai，j表示落在单元格G(i，j)内的实际观测点个数，用Bi，j表示由模型预测得到的落在单元格G(i，j)的点的个数(即预测频数)，其中i，j=1，2，…，k，则评价Copula函数对模型拟合度的χ2检验统计量M表示为:

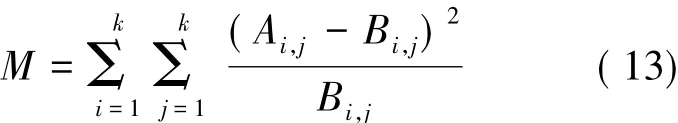
统计量M服从自由度为(k－1)2的χ2分布。

五、实证研究

(一)数据选取与基本特征

本文选取上证综指和深证成指的收盘价为研究对象，将它们分别记为SH和SZ。日收盘价的对数收益率{RLt}定义公式为:RLn，t=ln Pn，tln Pn，t－1，其中为收盘价序列，n代表沪市和深市，t=1，2，…，T，选取的样本时间段是19980928—20120323，本文使用Eviews6．0和Matlab R22010a进行计算。

表1 SH和SZ的对数收益率序列的基本统计量

由表1可以看出上证综指与深圳成指对数收益率序列具有以下特征:(1)样本峰度都远大于3，表明上证综指与深圳成指对数收益率呈现明显的尖峰厚尾性;(2)Jarque－Bera正态统计量的值远大于临界值5．99，表明序列的分布不是正态分布;(3)波动具有聚集性和左偏性。

(二)模型估计及检验

应用Gram-Charlier展开的准极大似然估计方法对GJRSK-M模型进行参数估计:(1)均值方程SH和ZH的估计结果中系数α1分别为－1．423 5 (－1．423 6)和0．294 6(0．294 6)统计不显著，说明在沪深两市中，不存在明显的方差风险溢价现象;而系数α2为0．000 9(4．273 6)和－0．000 4 (－4．873)，α3为0．000 6(12．748)和0．000 6 (13．259)是显著的，说明两市存在明显的偏度和峰度风险溢价现象，且偏度的风险溢价要大于峰度的风险溢价。可以看到α1＞α2＞α3，如果α1是显著的，则意味着投资者要将方差风险视为是最重要的，承担方差风险理应获得的较高的回报，但也不能忽略偏度和峰度风险。(2)方差方程中系数都是显著的，SH和ZH估计方程中的β2为0．948 7和0．955 6比β1(0．086 5和0．075 8)大得多，说明波动主要由前一天的波动决定，有明显的波动连续性;β3为0．086 4(13．456 9)和0．043 6 (28．339 6)显著大于0，说明沪深两市之间方差存在波动的杠杆效应，负的冲击将比相同程度的正的冲击导致更大程度的波动或者导致更多极值事件的出现。(3)偏度和偏度方程中，系数都是显著的，与方差方程的结果类似，都存在偏度和峰度的波动持续性以及杠杆效应。

利用上面GJRSK-M模型得到的条件高阶矩波动率估计序列，结合遗传算法对M-Copula函数进行极大似然估计，参数估计结果为:α=34．871 2，β=32．823 5，λ=18．493 1，wG=0．662 9，wCl= 0．330 1，wF=0．00 7，似然估计值为3 008．7，而统计量M为1 987．5。

从两市指数对数收益率序列相依结构模型参数的估计值来看，估计的参数都是非常显著的，Gumble函数占主要的权重，说明两市场的指数收益之间表现为上尾高、下尾低的较强的正相依结构。也就是说两市场同涨同跌;同时对于极端的波动又表现为非对称的上尾高、下尾低的特征，即两市大涨的概率要大于大跌的概率。Clayton函数的权重为0．330 1，说明两市的下尾变化的相关性不容忽视，即两个市场在处于熊市时期时，会有同步增强的相依性;而由Frank函数的权重系数可知，M-Copula-GJRSK-M对刻画两市对称的正相依或对称的负相依不显著。

(三)实证结果分析

本文基于资产的高阶矩风险的非对称性，将GJRSK-M模型与M-Copula函数相结合，建立了基于边缘分布的高阶矩非对称风险的相依结构模型，研究沪深股市的指数对数收益率之间的相依关系。研究发现:上证综指和深圳成指对数收益率存在高阶矩风险，虽然条件方差风险溢价显著性不强，但如果其溢价现象存在，则风险的由高到低顺序是:条件方差风险、条件偏度风险、条件峰度风险;沪深两市还存在风险的非对称性，即指数下跌时，条件方差风险和条件高阶矩风险会增大。在相依结构方面，上证综指和深圳成指的指数对数收益率之间表现出上尾高、下尾低的非对称的正相依的特征，说明在极端情况下，两市暴涨的概率要大于暴跌的概率，这可能与我国股市正在处于一个发展的上升过程有关。

六、结束语

金融市场风险因素相依结构的研究是金融市场风险分析的重要内容之一，现有很多研究也对股市之间的相依性关系进行了探讨，但是在结合Copula函数考虑边缘分布时，很少考虑金融资产的高阶矩波动对资产价格的影响，对高阶矩风险的研究还没有做够给予足够的关注和重视，对资产高阶矩风险的相依关系研究的相关论文更是很少。下一步可将二维的M-Copula-GJRSK-M模型向多维扩展，并且将此模型应用于投资组合领域。

［1］Samuelson P．The fundamental approximation of theorem of protfolio analysis in terms of means，variance and highermoments［J］．Review of Economic Studyies，1970，37(4):537-542．

［2］Lim K G．A new test of the three-moment capital assetpricingmodel［J］．Journal of Financial and Quantitative Analysis，1989，24(2):205-216．

［3］Jondeau E，RockingerM．Conditional volatility，skewness，and kurtosis:existence，persistence，and Comovements．Journal of Economic Dynamics and Control，2003，27 (10):1699-1737．

［4］Davies RJ，WKat HM，Lu S．Fund of Hedge Funds protfolio selection:a multiple-objective Approach［J］．Journal of Derivatives＆Hedge Funds，2004，15:91-115．

［5］Leno A，Rubio G，Serna G．Autoregresive conditional volatility，skewness and kurtosis．The Quarterly Review of Economics and Finance，2005，45(4-5):599-618．

［6］许启发．高阶矩波动建模及应用［J］．数量经济技术经济研究，2006(12):135-145．

［7］许启发，张世英．多元条件高阶矩波动模型研究［J］．系统工程学报，2007(1):38-52．

［8］蒋翠侠，许启发，张世英．金融市场条件高阶矩风险与动态组合投资．中国管理科学［J］．2007(1):67-93．

［9］蒋翠侠，张世英．基于条件Copula的高阶矩波动性建模及应用［J］．财政金融研究，2008，22(3):53-60．

［10］王鹏，王建琼，魏宇．自回归条件发方差-偏度-峰度:一个新的模型［J］．管理工程学报，2009，12(5): 121-129．

［11］Sklar，A．Functions de repartition an dimensions et leurs marges［J］．Publ．Inst．Statist，Univ，Paris，1959，33 (8):229-231．

［12］韦艳华，张世英．Copula理论及其在金融分析上的应用［M］．北京:清华大学出版社，2008．

［13］Hu L．Essays in Economics with applications in macroeconomic and financialmodelling［D］．Yale University，2002:634-656．

(责任编校:朱德东，夏东)

Analysis of the Interdependence between Shanghai and Shenzhen Stock Market Based on M-Copula-GJRSK-M Model

SHEN Jian-ping，SUN Fei，HUANG Min
(School of Mathematics and Statistics，Chongqing University，Chongqing 401331，China)

Financial assets notonly have variance risk，butalso have time-varying skewness risk and kurtosis risk，whichmakes risk change study very limited if only based on the firstor the secondmomentof the financialassets．GJRSK-M model is an effective tool for highermoments risk description of the financial assets and can fit for the distribution of individual financial assets，however，M-Copula function can connectmarginal distribution of portfolio financial assets，thus，this paper establishesM-Copula-GJRSK-M model to study the interdependence between Shanghaiand Shenzhen stockmarket．The empirical results show that there are highermoment risk and risk asymmetry of the logarithm earnings rate of Shanghai composite index and Shenzhen component index，i．e，conditional variance risk and conditional highermoment risk increasewhen the index falls，furthermore，the probability for the index rise of the two stock markets is bigger than that of the index fall under the extreme condition．

M-Copula function;GJRSK-M model;highermoments risk

F224．0;F830．91

A

1672-0598(2014)01-0016-06

12．3969/j．issn．1672-0598．2014．01．003

2013-10-29

申建平(1989—)，男，云南人;重庆大学数学与统计学院硕士研究生，主要从事金融工程研究。