一类双层规划问题的遗传算法求解

于建平，杜纲

(天津大学管理与经济学部，天津 300072)

一类双层规划问题的遗传算法求解

于建平，杜纲

(天津大学管理与经济学部，天津 300072)

研究了一类值型双层规划问题，即下层规划将其目标函数最优值返回给上层规划。在双层规划的解的基本概念的基础上，给出了一种双层的遗传算法求解方法。该方法是在上层问题的遗传算法中嵌套一个求解下层问题的遗传算法。用实际的算例来验证算法设计的可行性，同时通过与传统算法结果的对比来表明该算法的计算效果。最后，指出了该算法的一些不足。

双层规划;解型;值型;遗传算法;可行性

随着工程设计的发展，很多重要的设计呈现出复杂的主从结构，难以用单层优化模型来描述，因而双层规划显得不可替代。近年来，已有一些研究探讨了双层规划在工程设计中的应用，如Shabde和Hoo［1］基于双层规划的框架建立了化工产品设计与过程控制协同优化的模型。作为双层规划中的一种重要情形，主从对策方法也得到了一些应用，如Hernandez等［2］在一个设计与维护的关联优化问题上应用了主从对策方法。

双层规划(bilevel programming)也称双层优化，是指模型的约束中包含子优化问题的数学规划，最早由Bracken和McGill［3］提出，由于它抽象了包括主从对策在内的一类重要的递阶决策问题而具有广泛的实际背景。双层规划理论取得了较快的发展并成为数学规划领域中的重要分支。双层规划虽然可以作为数学规划的一种推广形式，但它与普通数学规划有着很大的不同。由于模型的上层中含有下层的最优解或最优值函数，使得模型易成为非光滑的优化问题，即使是线性的双层规划也是NP－难的［4］，并且当上层的约束中含有下层的最优解时，其可行域可能是不连通的。目前，双层规划的求解方法主要有针对特殊线性情形的K次最好法［5］，可采用K－T条件代替下层问题而转化为单层规划的方法［6］，利用对偶间隙构造罚函数而转化为单层问题的方法［7］以及智能算法［8］等。由于一般双层规划求解的复杂性，Lai［9］等提出的满意解法受到关注，该方法最初主要针对线性问题，后来被推广到非线性的情形［10］。

虽然对于双层规划求解的研究很多，但常规的数学求解还仅限于一些特殊的问题。因本文提出的模型较复杂，故拟采用遗传算法进行求解。遗传算法是模拟生物进化中的选择、交叉、变异过程来求解复杂优化问题的一种有效的方法，具有全局收敛性、鲁棒性，且简单通用［11］，但是针对不同的问题往往需要自身设定相应的遗传算子。遗传算法求解双层规划分为2方面:一是若模型属于线性或非线性凸等特殊的双层规划，可根据情况采用K次最好法或由K－T条件转化为单层规划求解［12－14］;二是直接求解。这其中包括只用遗传算法求解［15］和混合遗传算法求解［16］。尽管国内外已有很多关于用遗传算法求解双层规划的文献，但其研究结果并不具有普适性。正如Coello［17］在其文章中所提到的:对于任何有约束的优化问题，没有任何一个约束控制的方法可以使遗传算法应用一切问题，每一个约束控制方法都有一定的适用范围。

因此，本文只针对一类双层规划问题设计了相应的遗传算法。写作结构如下:第2部分是对问题背景的描述;第3部分提出了基于遗传算法的求解方法;第4部分进行算例验证，并与之前的研究做了效果比较;第5部分对文章进行简要总结，阐述了结论和未来研究的方向。

1 问题描述

1.1 双层规划的一般模型和基本概念

王广民等［18］根据国内外有关双层规划的文献，给出了其数学模型和基本概念。双层规划的一般模型如下:

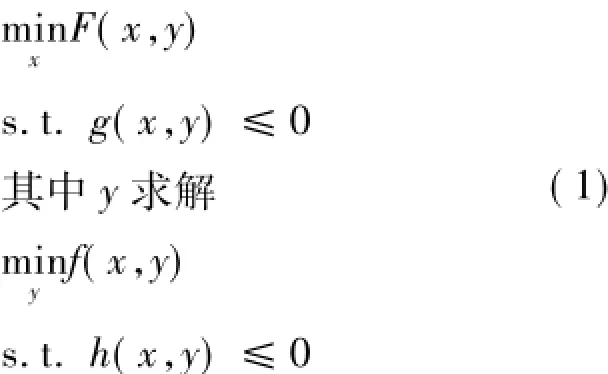
其中:x∈Rn，y∈Rm分别为上层和下层规划问题的决策变量;F，f:Rn×Rm→R分别为上层和下层规划问题的目标函数;g( h):Rn×Rm→Rp(Rq)分别为上层和下层规划问题的约束条件。

上述的数学模型是解型双层规划的一般形式，即上层规划问题的目标函数和约束条件不仅与上层规划的决策变量有关，还依赖于下层规划问题的最优解，而下层规划的最优解又受上层决策变量的影响。

一些基本概念的定义如下:

1)双层规划问题的约束域:Ω={(x，y)| ( x，y)≤0，h( x，y)≤0}。

2)对于任意给定的x，下层规划问题的可行域:Ω(x)={y|h( x，y)≤0}。

3)对于任意给定的x，下层规划问题的合理反应集即下层问题的最优解集:M(x)={y|y∈rg min{ f( x，y)}，y∈Ω(x)}。

4)双层规划的诱导域即上层规划的可行域: R={(x，y)|(x，y)∈Ω，y∈M(x)}。

5)双层规划问题的最优解(x*，y*)满足∀(x，y)∈IR有F( x*，y*)≤F( x，y)。

整个双层规划问题的复杂性取决于上下层规划的特性，线性双层规划问题(即上下层规划问题的目标函数和约束条件都是线性的)最为简单，且易求解;相反，非线性双层规划不易求解，而且目标函数往往不可微、不连续、多峰，诱导域非凸、不连通，合理反应集M(x)为非单点集，这些都进一步增加了求解的难度。

1.2 问题的提出

本文根据处理工程设计问题中的实际需求，提出了一种值型双层规划问题，即上层规划问题做出决策并反应给下层，下层规划问题根据上层规划的决策得出自身目标函数的最优值，然后将最优值反应给上层规划。它的一般形式如下:

其中:lbx∈Rn(lby∈Rm)和ubx∈Rn(uby∈Rm)分别为决策变量x(y)的下界和上界;v(x):Rn×Rm→R为上层规划问题的决策x固定时下层规划问题的目标函数最优值。

上述双层规划的上层规划问题的目标函数不仅与上层规划的决策变量有关，而且依赖于下层规划问题的目标函数的最优值，而下层规划的最优值又受上层决策变量的影响;上层问题的约束条件不含有下层问题的决策变量;x和y都有上下界约束;x和y既可以是连续变量，也可以是离散变量。此类问题的基本概念与1.1节中双层规划的基本概念是一致的，但它可避免当下层规划为多峰问题时无法找到双层规划问题的全局最优解的情况。

2 算法设计

遗传算法是求解复杂优化问题的一种新型有效的方法。已有学者将其应用到求解双层规划的问题上。本文依据双层规划的解的概念和遗传算法的一般流程设计了一种求解1.2中问题的方法。

2.1 遗传算法设计流程

为了有效地求解模型(2)，本文设计了一个嵌套的遗传算法。该方法先产生上层规划的初始种群，验证其可行性，然后将每一个可行的上层决策x代入下层规划，下层规划利用遗传算法求解出最优决策y*(x)和最优值v(x)，同时下层把最优值v(x)返回给上层来求解上层决策的适应度值，随后将上层决策种群进行选择、交叉、变异，按照此步骤循环一定的次数后，得到上层规划的最优解x*和相应的下层问题的最优解()。上述方法的流程如图1所示。

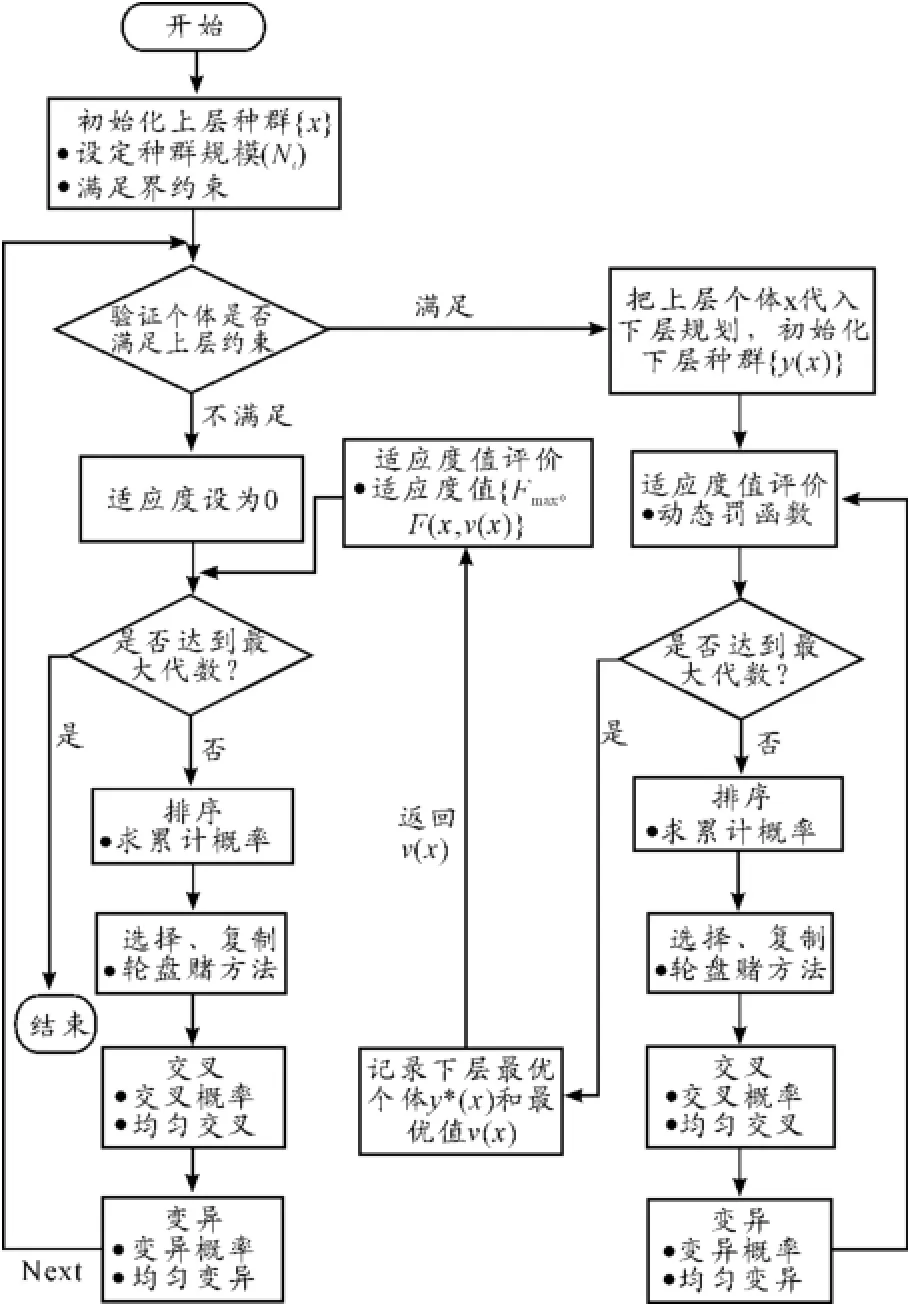
图1 遗传算法求解流程

2.2 遗传算法的具体步骤

步骤1(初始化和编码)在上层规划的界约束上随机生成Nl个初始解。对于连续型变量，本文采用二进制编码，每个变量的编码长度根据求解精度和其上下界来确定;对于离散型的变量，本文采用有序数组的标记方法，即实数编码。例如，如果变量x1为一离散变量，其取值为数列{x11，x12，…，x1n1}中的数，n1为数列中的元素个数，具体编码策略如图2所示。

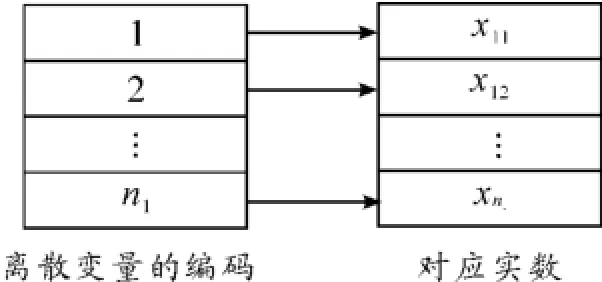
图2 离散型变量的编码策略

步骤2(嵌套遗传算法)针对上层规划种群的每个可行个体x，利用遗传算法求解下层规划问题:首先设定遗传代数为当前外层循环次数，同时设定下层遗传算法的个体数量Nf;然后对下层规划进行初始化(编码方式同步骤1)，基于下层优化目标函数进行个体评价(评价采用动态罚函数方法［19］)，再进行选择操作、交叉操作以及变异操作;最后求得上层种群可行个体所对应的下层规划的最优解y*(x)和最优值v(x)，记录最优解并将最优值返回上层。

步骤3(上层规划的适应度值)对于上层规划的可行个体x，通过嵌套的遗传算法得到对应的下层问题的最优值v(x);然后代入上层问题的目标函数F( x，v(x ));最后比较所有可行个体对应的目标函数值，得出最大的一个，并记为Fmax，用当前代的Fmax与上一代的Fmax做比较。如果当前代的Fmax大，就保留;如果上一代的Fmax大，就用其替代。利用式子Fmax－F( x，v(x ))计算每一个可行个体的适应度值，对于不可行个体，则设其适应度值为零。

步骤4(终止条件)如果当前代达到最大迭代次数，则停止，并将当前的最优个体和其对应的下层问题的最优解作为双层规划的最优解记录下来;如果未达到最大迭代次数，则继续步骤5。

步骤5(选择、交叉、变异)设定交叉概率和变异概率，针对上层问题的种群分别采用轮盘赌方法、均匀交叉、均匀变异的方法进行选择、交叉、变异，记录变异后的种群为新一代的种群，然后重复步骤2。

3 数值实验

为了验证嵌套遗传算法的计算性能以及鲁棒性，本文将其与传统的双层规划求解方法进行比较。为了更好地显示算法的可行性和效果，本文选取了3种不同的算例进行测试。第1个为线性双层规划问题(上下层规划都为线性规划);第2个是下层为非线性双层规划问题;第3个为混合型的双层规划问题。上下层遗传算法的参数设置如下:种群规模为50，迭代次数为200，二进制编码的精度为0.01，交叉概率为0.8，变异概率为0.01。

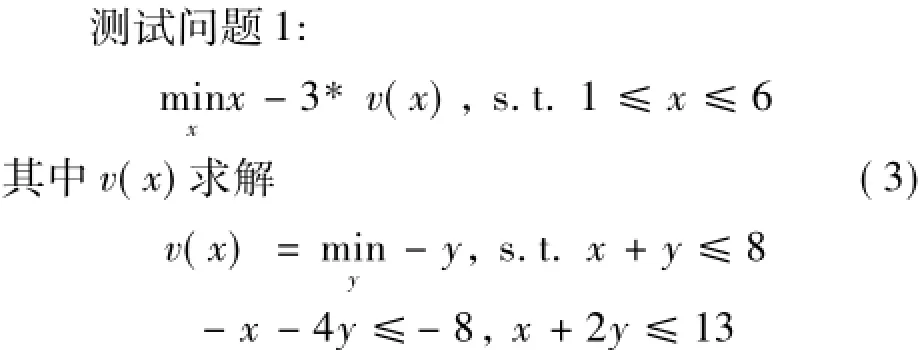
图3 测试问题1的遗传算法迭代图像

测试问题2:

测试问题2是一个非线性双层规划问题，已有方法求解的最优值和最优解为［21］:

本文最优计算结果为(遗传算法迭代图像如图4所示):

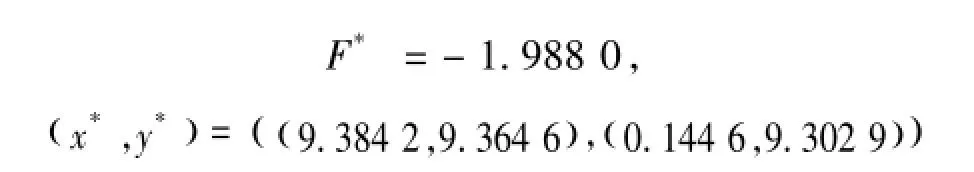
从两种结果来看:最优解的差别比较大，而最优值的差距仍然在0.01左右。这一方面说明了此问题有可能是一个多峰问题，另一方面也说明了本文算法的可行性和有效性。

图4 测试问题2的遗传算法迭代图像

测试问题3:

测试问题3是一个混合型双层规划问题，已有方法求解的最优值和最优解为［22］:

本文最优计算结果为(遗传算法迭代图像如图5所示):

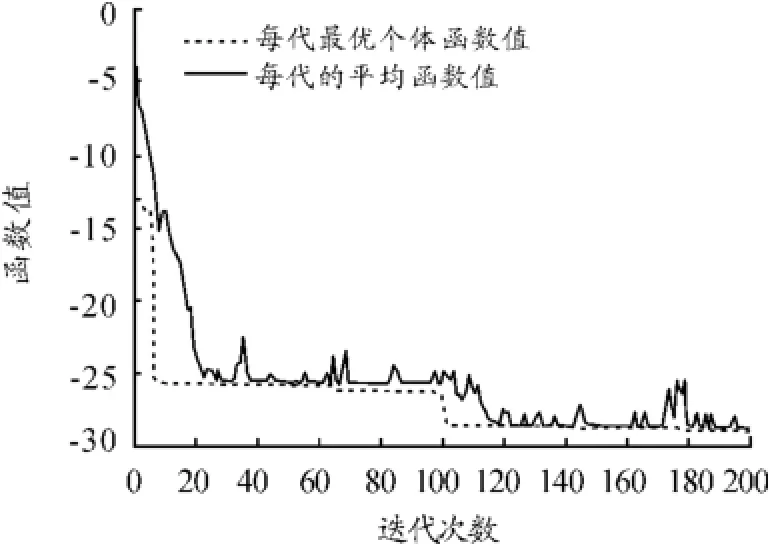
图5 测试问题3的遗传算法迭代图像

由两种结果可以看出:最优值的差距不足0.01。这也进一步说明了本文遗传算法的有效性，它不仅可以求解连续型的双层规划问题，也能求解混合型的双层规划问题。

4 结束语

本文根据值型双层规划的特点——可以避免下层规划为多峰问题时双层规划无解的情况，提出了一种嵌套的遗传算法，并通过算例验证了算法的效果及其可行性，给解决实际问题提供了一个有效的计算方法。虽然本文的算法在求解值型双层规划时具有一定的适用性，但是当上下层规划问题非常复杂、可行域比较小，而搜索范围过大时，往往不易找到可行解。这也是本文没有在模型(2)中加入等式约束的原因。在今后的研究中可尝试加入一种使初始化种群在可行域中产生的方法［20］，即确定可行域的方法，使交叉、变异算子都为可行算子［21］，即交叉、变异后的个体都为可行个体，或是采用某种修复策略将不可行的个体变为可行个体。

［1］Vikram，Shabde，Hoo.Optimum controller design for a spray drying process［J］.Control Engineering Practice，2008，16(5):541－552.

［2］Hernandez，Seepersad，Mistree.Designing for maintenance:a game theoretic approach［J］.Eng.Opt.，2002，34 (6):561－577.

［3］Bracken J，JTMcGill.Mathematical programs with optimization problems in the constraints［J］.Operations Research，1973，21(1):37－44.

［4］Jeroslow R G.The polynomial hierarchy and a simple model for competitive analysis［J］.Mathematical programming，1985，32(2):146－164.

［5］Bialas W F，Karwan M H.Two－level Linear Programming［J］.Management Science，1984，30(8):1004－1021.

［6］Fortuny－Amat J，McCarl B.A representation and economic interpretation of a two－level programming problem［J］.Journal of the Operational Research Society，1981，32 (9):783－792.

［7］Anandalingam G，White D J.A solution method for the linear static Stackelberg problem using penalty functions［J］.IEEE Transactions on Automatic Control，1990，35 (10):1170－1173.

［8］Mathieu R，Pittard L，Anandalingam G.Genetic algorithm based approach to bi－level linear programming［J］.RAIRO Rechercheoperationnelle，1994，28(1):1－21.

［9］Lai Y J.Hierarchical optimization:A satisfactory solution［J］.Fuzzy sets and systems，1996，77(3):321－335.

［10］OE Emam.A fuzzy approach for bi－level integer non－linear programming problem［J］.Applied mathematics and computation，2006，172(1):62－71.

［11］席裕庚，柴天佑.遗传算法综述［J］.控制理论与应用，1996(6):697－708.

［12］Hejazi S R，AMemariani G Jahanshahloo.Linear bilevel programming solution by genetic algorithm［J］.Computers＆Operations Research，2002，29(13):1913－1925.

［13］常永明，王宇平.求解一类特殊的双层规划问题的遗传算法［J］.计算机工程与应用，2009，45(3):45－47.

［14］王越，许全文，黄丽丰.基于改进遗传算法的连续函数优化［J］.重庆理工大学学报:自然科学版，2011，25 (2):62－67.

［15］Oduguwa V，Roy R.Bi－level Optimisation using Genetic Algorithm［C］//Proceedings of the 2002 IEEE International Conference on Artificial Intelligence Systems.［S.l.］:［s.n.］，2002:322－327.

［16］李和成，王宇平.几类非线性双层规划问题的混合遗传算法［J］.系统工程与电子技术，2008，30(6):1168－1172.

［17］Coello.Theoretical and numerical constraint－handling techniques used with evolutionary algorithms:a survey of the state of the art［J］.Computer methods in applied mechanics and engineering，2002，191(11):1245－1287.

［18］王广民，万仲平，王先甲.二(双)层规划综述［J］.数学进展，2007，36(5):513－529.

［19］Kramer O.A review of constraint－handling techniques for evolution strategies［J］.Applied Computational Intelligence and Soft Computing，2010:1－11.

［20］Li X，Du G.Inequality constraint handling in genetic algorithms using a boundary simulation method［J］.Computers＆Operations Research，2012，39(3):521－540.

［21］Liu B.Stackelberg－Nash equilibrium for multilevel programming with multiple followers using genetic algorithms［J］.Computers＆Mathematics with Applications，1998，36(7):79－89.

［22］宿洁，马建华.两类线性双层规划的算法［J］.经济数学，2002，19(1):68－76.

(责任编辑 刘舸)

Genetic Algorithm for Solving a Class of Bi-level Programming Problems

YU Jian－ping，DU Gang
(College of Management and Economics，Tianjin University，Tianjin 300072，China)

This paper studies a kind of value－type bi－level programming，namely the lower programming returns its optimal value of the objective function to upper level.Based on the basic concept of solution of the bi－level programming，we propose a method of two－level genetic algorithm.This method nests a genetic algorithm in genetic algorithm of the upper problem to solve a problem in the lower.Then，this paper uses practical examples to verify the feasibility of algorithm design，while the computation result of algorithm design is compared with the traditional algorithm to illustrate the calculating effectiveness.In the end，this paper puts forward some disadvantages of the algorithm.

bi－level programming;solution－type;value－type;genetic algorithm;feasibility

TP 18;O221

A

1674－8425(2014)04－0093－06

10.3969/j.issn.1674－8425(z).2014.04.020

2013－12－15

国家自然科学基金资助项目(71071104)

于建平(1987—)，男，硕士研究生，主要从事工业工程方面的研究。

于建平，杜纲.一类双层规划问题的遗传算法求解［J］.重庆理工大学学报:自然科学版，2014(4):93－98.Citation format:YU Jian－ping，DU Gang.Genetic Algorithm for Solving a Class of Bi－level Programming Problems［J］.Journal of Chongqing University of Technology:Natural Science，2014(4):93－98.