分布式检测融合系统的空间优化问题

彭会萍，曹晓军

(兰州商学院商务信息技术实验教学中心，兰州 730020)

分布式检测融合系统的空间优化问题

彭会萍，曹晓军

(兰州商学院商务信息技术实验教学中心，兰州 730020)

提出了一种分布式检测融合系统的空间优化方法。将局部检测器决策空间进行再划分并建立可信度，由局部检测器将决策结果与可信度同时送达融合中心进行融合。仿真结果表明:采用该方法的检测性能得到了较好的改善，且改善效果与再划分的水平数有关。同时仿真了各局部检测器在不同的相关系数下的融合结果。

分布式检测系统;空间再划分;可信度;相关系数

分布式目标检测系统由于具有通讯带宽窄、决策可靠性高、系统成本低且易实现等优点，在无线传感器网络、声纳、雷达、敌我识别等众多领域有着广泛应用，是现代测量技术研究的热点领域。

分布式检测系统中的传感器判决门限和融合中心的决策算法可以直接影响决策结果，因此传感器判决门限的确定算法是一个研究热点。文献［1］采用穷举算法确定判决门限，并将其用于解决图像和语音识别问题，但效率不高;文献［2－3］使用退火算法、遗传算法解决了MAP算法在先验信息未知条件下的应用问题;文献［3－4］给出了一种最优检测时的融合规则和各传感器的量化规则;文献［3，5］提出了一些对传感器观测空间进行最优再划分的方法，虽然性能较好，但是计算量很大。本文提出一种新的对各传感器的观测空间进行再划分的方法，仿真结果表明该方法计算过程简单，且能较好地提高融合中心的检测性能。

1 问题描述

考虑一个具有H1(目标存在)和H0(目标不存在)的二元假设检验问题，2个假设的先验概率分别是P1和P0，并令第i个局部检测器的检测统计量为ri，其相应的判决结果为ui，如图1所示，其局部决策空间为Ωi={所有可能的ri}。假设各局部检测器的决策门限已确定，即将局部决策空间划分为Ωi0和Ωi1，且满足Ωi=Ωi0∪Ωi1及Ωi0∩Ωi1= ø。因此，局部检测器的判决规则为:

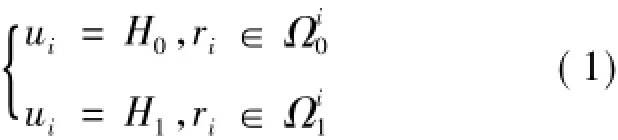
其中，ui为局部检测器的判决结果。在此决策规则下，第i个局部检测器的虚警概率、检测概率和漏警概率分别为:

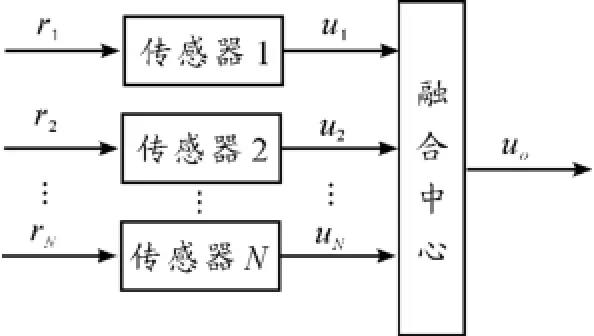
图1 分布式并行检测系统结构

2 局部检测器决策空间的再划分

令各局部检测器的判决规则已定，且是最优的。记各局部检测器的检测统计量为ri，其判决门限值为Ti，且ri的条件概率密度函数为p(ri|H0)和p(ri|H1)，如图2所示。

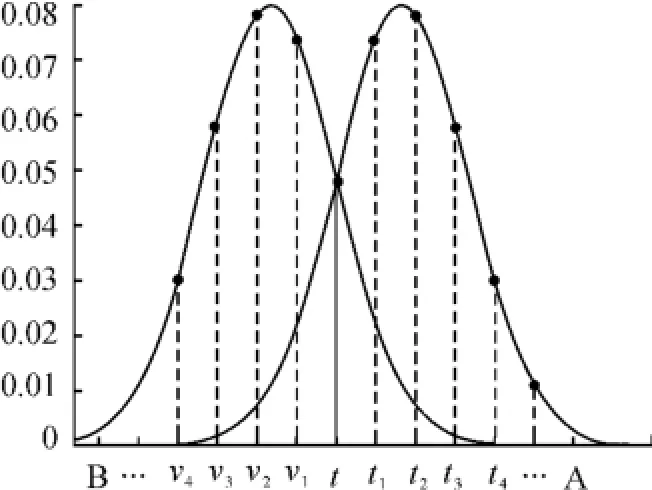
图2 局部检测器统计量的条件概率密度函数

局部检测器的判决过程实质上就是将其检测统计量ri与门限Ti进行比较，当ri≥Ti时，判决目标存在;当ri＜Ti时，判决目标不存在。

检测统计量ri超过或低于判决阈值Ti的程度反映了该传感器判决的可信度。因此，为了进一步提高系统的性能，各局部检测器融合中心在传送决策结果ui的同时，还传送了该传感器的决策可信度Ci，k。

2.1 判决可信度

对于单个传感器判决的可信度，可以通过ri相对于Ti的偏差，对观测空间Ωi0和Ωi1进行有限位的量化来获得，量化位数由系统的通信能力决定。当ri≥Tk时，为了反映ri超过Tk的程度，仅需对［Tk，∞)进行量化。显然，若存在一个数值Ak，使得P(ri≥Ak|H1)≈0，则为了充分反映判决结果ui=1的可信度，仅需对［Tk，Ak］进行量化。同理，当ri＜Tk时，如果存在一个数Bk，使得P(ri＜Bk|H0)≈0，则为了充分反映ui=0的可信度，仅需对区间［Bk，Tk］进行量化。

设单个传感器的判决可信度Ci，k用M位二进制数表示。将［Tk，Ak］分成M份，记为Tk，1，Tk，2，…，Tk，M，并将对应的空间记为H11，H12，…H1M;将［Bk，Tk］也分成M份，记为Tk，－1，Tk，－2，…，Tk，－M，并将对应的空间记为H01，H02，…H0M。则判决ui=1的可信度为:

判决ui=－1的可信度为:

2.2 单个传感器接收信息及其判决阈值的界定

考虑融合系统由N部传感器组成，对于单部传感器，其接收机输出服从高斯分布:

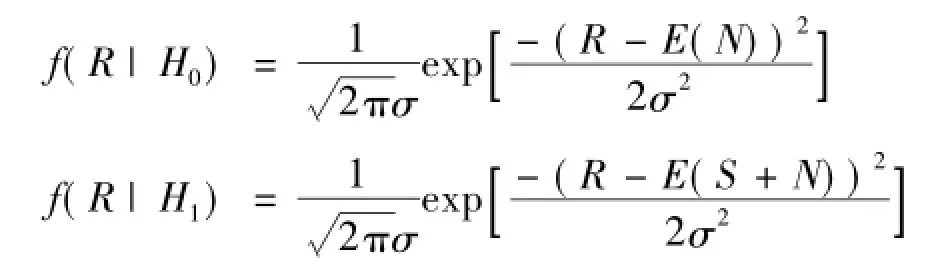
式中:E(S+N)为接收信号加噪声的均值;E(N)为噪声的均值;σ为噪声均方差。

设第i部接收机输出端检测门限为Ti，要使传感器报警的误码率最小，必须满足f(R|H0)= f(R|H1)，根据此式可以求解出判决阈值Ti。

2.3 融合算法

考虑到每个传感器决策的可信度Ci，k，则融合中心的观测向量可表示为在各局部检测器的观测和决策都是统计独立的条件下，融合中心的似然比为C至融合中心，系统融合中心根据判决向量U=

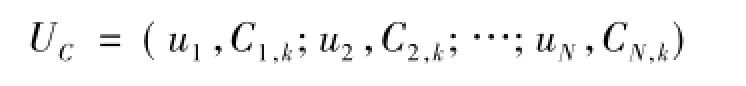
3 系统融合及仿真

3.1 案例

令传感器的个数N=3，并设各传感器的输出信噪比分别为SNR1=2.6 dB，SNR2=3.0 dB，SNR3=3.5 dB。各传感器的虚警概率相同为PF= 10－4，且各传感器相互独立，即相关系数ρ=0。

3.2 仿真结果分析

在空间划分阶数为1，各个传感器相互独立的情况下，仿真结果如图3所示。对于各传感器检测性能相差不大的情况，融合系统的检测性能优于任一单一传感器。

图4表示在不同空间阶数划分情况下的仿真结果。对观测空间再划分后，融合中心的检测性能有所变化。例如M=1和M=7比较，当M较大时，检测性能有较大的改善;当M过大时，检测性能改善不明显，且M越大，计算复杂性随N(M－1)呈指数增加。

为了探讨融合系统的检测性能与各传感器输出相关性之间的关系，设ρ1，2=ρ1，3=ρ2，3=ρ，并分别令ρ=0，ρ=0.5，ρ=0.8，在M=1和M=3， SNR1=SNR2=SNR3=5 dB时，仿真结果如图5、图6所示。

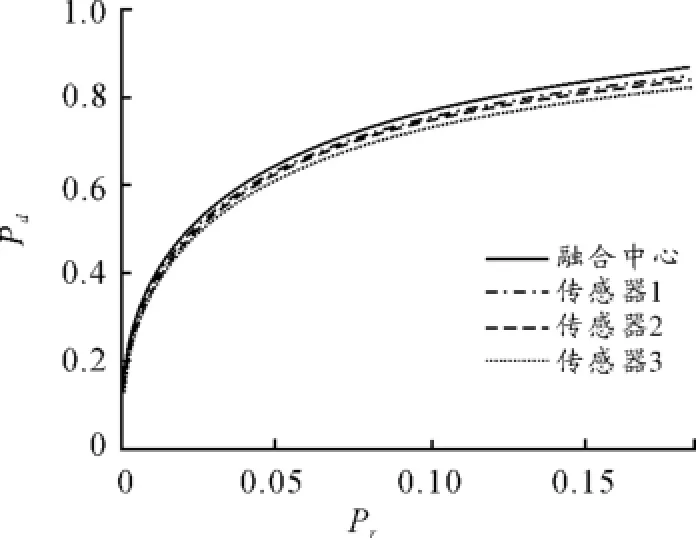
图3 M=1，ρ=0时融合中心的ROC

图4 M=1，3，5，7时的融合中心的ROC

图5 M=1时融合中心ROC

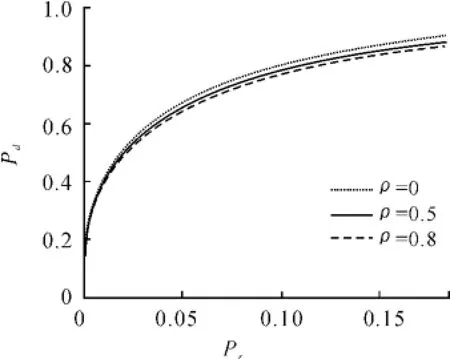
图6 M=3时融合中心ROC

4 结束语

本文通过对分布式检测融合系统的空间优化来确定传感器判决门限值。较之现有的方法，本方法对融合中心检测性能有较大的改善。

仿真结果表明:融合系统空间划分的阶数M对融合中心检测性能的改善有不同程度的影响。随着M的增大，其改善效果越来越不明显，而且会使得计算量有较大幅度的增长，因此M的取值应以大于1且小于7为比较合理。

［1］张磊，杨建峰，薛彬，等.改进的最大后验概率估计法实现单幅图像超分辨率重建［J］.激光与光电子学进展，2011，48(1):0110003.

［2］刘明辉，王磊，党林阁，等.非确定先验信息的贝叶斯网构学习方法［J］.计算机工程，2010，36(5):165－167.

［3］金俊丽，赵川，杨洁.基于EM－GA改进贝叶斯网络的研究及应用［J］.计算机应用研究，2010，27(4):1360－1362.

［4］相明.分布式多传感器检测数据融合算法及其应用研究［D］.西安:西北工业大学，1999.

［5］Lee C C.Optimum Local Decision Space Partitioning for Distributed Detection［J］.IEEE Trans.On AES，1989，25 (4).

［6］Warren Douglas，Willett Peter.Optimum Quantization for Detector Fusion:Some Proofs，Examples，and Pathology［M］.USA:The Franklin Institute，1998.

［7］南利平.通信原理简明教程［M］.北京:清华大学出版社，2007(8):240－243.

［8］王宏飞.被动传感器信息融合［D］.南京:南京理工大学，2003.

［9］李良群.信息融合系统中的目标跟踪及数据关联技术研究［D］.西安:西安电子科技大学，2007.

［10］胡学海，王厚军.分布式目标检测融合决策优化算法［J］.电子科技大学学报，2013，42(3):375－379.

(责任编辑 杨黎丽)

Space Optimization Problem of Distributed Detection Fusion System

PENG Hui－ping，CAO Xiao－jun
(Experimental Teaching Center of Business Information Technology，Lanzhou University of Finance and Economics，Lanzhou 730020，China)

This paper proposed a kind of distributed detection fusion system of space optimization method，and simulated this method.The local detector decision space was re－divided，and the credibility was established.The decision results and credibility were conveyed to fusion center for fusion.The simulation results show that this detection performance will be better improved，and the effect depends on the re－divided level number.This paper also simulates the fusion results in different correlation coefficient.

distributed detection system;space re－divide;credibility;correlation coefficient

TN911.72

A

1674－8425(2014)04－0089－04

10.3969/j.issn.1674－8425(z).2014.04.019

2014－01－16

甘肃省科技计划资助项目(1208RJZA105);甘肃省教育厅项目(1005B－12)

彭会萍(1971—)，女，甘肃正宁人，硕士，教授，主要从事信息融合与数据挖掘方面研究。

彭会萍，曹晓军.分布式检测融合系统的空间优化问题［J］.重庆理工大学学报:自然科学版，2014(4):89－92.

format:PENG Hui－ping，CAO Xiao－jun.Space Optimization Problem of Distributed Detection Fusion System［J］.Journal of Chongqing University of Technology:Natural Science，2014(4):89－92.