利用极小作用原理研究一类二阶系统的周期解

王少敏

(大理学院数学与计算机学院，云南大理 671000)

利用极小作用原理研究一类二阶系统的周期解

王少敏

(大理学院数学与计算机学院，云南大理 671000)

研究了一类非自治二阶哈密顿系统周期解的存在性，在非线性项F(t，x)= F1(t，x)+F2(t，x)满足条件(A)及F1(t，x)，F2(t，x)分别满足一定条件时，通过使用极小作用原理获得了一个新的周期解的存在性定理。

周期解;极小作用原理;二阶系统

1 主要结果

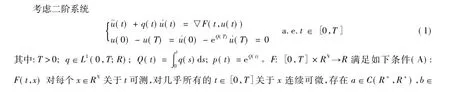
2 定理的证明

［1］Wu X，Chen Sh X，Teng K M.On variational methods for a class of damped vibration problems［J］.Nonlinear Anal，2008，68 (1):1432－1441.

［2］Rabinowitz P H.On subharmonic solutions of Hamiltonian systems［J］.Comm Pure Appl Math，1980，33(1):609－633.

［3］黄文念.一类二阶Hamilton系统周期解的存在性［J］.河南理工大学学报:自然科学版，2010，29(1):126－130.

［4］贾宏恩，刘喜兰.一类非自治二阶系统的周期解［J］.重庆交通大学学报:自然科学版，2009，28(2):330－332.

［5］Tang C L.Periodic solutions for non－autonomous second order systems with sublinear nonlinearity［J］.Proc Amer Math Soc，1998，126(1):3263－3270.

［6］Wu X P，Tang C L.Periodic solutions of nonautonomous second－order Hamiltonian systems with even－typed potentials［J］.Nonlinear Anal，2003，55:759－769.

［7］Ma J，Tang C L.Periodic solutions for some nonautonomous second－order systems［J］.J Math Anal Appl，2002，275(1):482－494.

［8］唐春雷，从志坚，孟世才.具有偶型位势的二阶系统周期解的存在性定理［J］.西南师范大学学报:自然科学版，2002，27 (5):637－640.

［9］赵军，高岩.二阶线性系统族的共同二次Lyapunov函数［J］.重庆师范大学学报:自然科学版，2012，29(4):52－56.

［10］Mawhin J，Willem M.Critical Point Theory and Hamiltonian Systems［M］.Berlin/New York:Springer－Verlag，1989.

Periodic Solutions for a Class of Second Order Systems by the Least Action Principle

WANG Shao－min
(Department of Mathematics and Computer，Dali University，Dali 671000，China)

Existence of periodic solutions for a class of non－autonomous second order Hamiltonian systems is studied.When the nonlinear term F(t，x)=F1(t，x)+F2(t，x)satisfies condition(A)and F1(t，x)，F2(t，x)satisfy many conditions，one new existence theorem of periodic solution is obtained by the least action principle.

periodic solutions;the least action principle;second order systems

O177.25

A

1674－8425(2014)03－0155－04

10.3969/j.issn.1674－8425(z).2014.03.029

2013－10－18

云南省科技厅应用基础项目(2011FZ167);云南省教育厅科学研究基金项目(09Y0367)

王少敏(1975—)，女，云南大理人，硕士，副教授，主要从事非线性分析的研究。

王少敏.利用极小作用原理研究一类二阶系统的周期解［J］.重庆理工大学学报:自然科学版，2014(3): 155－158.

format:WANG Shao－min.Periodic Solutions for a Class of Second Order Systems by the Least Action Principle［J］.Journal of Chongqing University of Technology:Natural Science，2014(3):155－158.