关于既有接触网大修中心锚结位置设置的探讨

黄 河

0 引言

在既有线接触网大修时，往往会遇到由于支柱跨距的调整而使整个锚段缩短或增长的情况。由此，该锚段内中心锚结位置若仍在既有位置，则可能由于锚段长度改变和线路情况变化引起线索张力增量变化导致线索张力不均和定位器、腕臂偏移量大等问题。本文对既有线接触网改造锚段长度变化后，重新设置中心锚结位置作一些分析和探讨。

1 中心锚结的安设

在两端装设补偿器的接触网锚段中，必须加设中心锚结。每个锚段中心锚结安设位置应根据线路情况和线索的张力增量计算确定。一般布置原则是使中心锚结固定点两侧线索的张力尽量相等，并尽可能靠近锚段中部。

当锚段全部在直线区段或整个锚段布置在曲线半径相同的曲线区段时，该锚段中心锚结应安设在锚段的中间位置。

当锚段布置在既有直线又有曲线且曲线半径不等的区段时，该锚段的中心锚结应设在曲线多、曲线半径小的一侧。在特殊情况下，锚段长度较短时（一般定为锚段长度800 m以下），可不设中心锚结，视为半个锚段，可将锚段一端硬锚，另一端线索安装补偿器，此时的硬锚就相当于中心锚结。

2 影响中锚位置的因素

在既有网大修时选择中心锚结位置时应充分考虑以下几方面：

（1）接触悬挂在线路坡道处，由于悬挂本身的重量沿下坡方向产生作用于悬挂的分力。

（2）曲线上因旋转腕臂偏转，出现对线索向某一方向的分力作用。

（3）一侧下锚转角过大时，会限制腕臂随温度的偏移。

（4）风力和受电弓对接触线的滑动摩擦力方向等。

（5）锚段长度变化和锚段位置变化后，线索由于线路情况发生变化而导致张力变化。

以上原因都可能造成中心锚结两端张力不平衡，有时可能会重叠出现，诱发接触悬挂向某一方向产生窜动。

3 中心锚结的重新安设

当锚段长度变化时，若中心锚结位置仍在原位，势必因中心锚结两端张力差过大而造成吊弦、腕臂偏移量过大。这里需要说明一点，接触网张力差是始终存在的，一般情况下（中锚位置适合），张力差值最多为最大张力的10%。

3.1 定位器形成的张力增量ΔTjW

定位器在温度变化时也因接触线产生伸长（或缩短）而发生偏转。在直线区段上，由于定位器对接触线张力变化影响很小（一般对1500 m长的锚段，其定位器产生的张力增量只有几十 N），可以忽略。因此，对于定位器产生的张力增量，只考虑曲线上的情况。

为了确定接触线因定位器的移动而引起的张力变化，需研究它们的平衡条件。

因为定位器的作用，在温度变化时，接触线产生张力增量ΔTjw，其受力情况如图1和图2所示[1]。

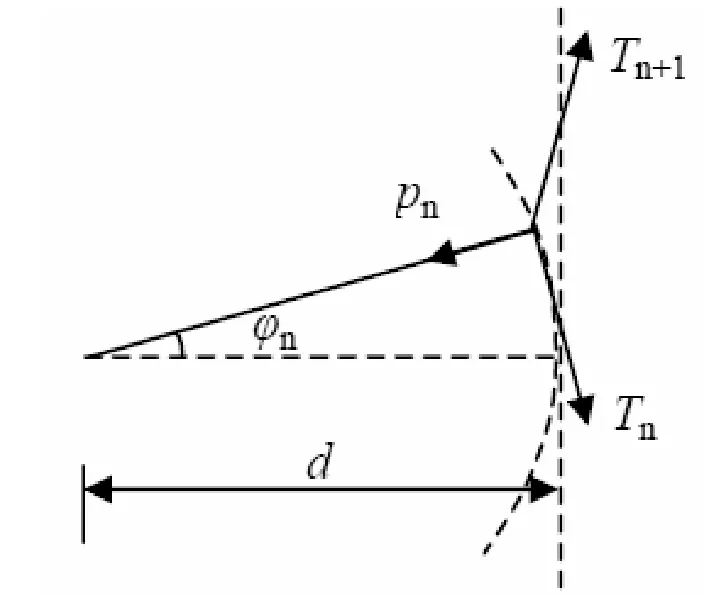
图1 定位器偏移示意图

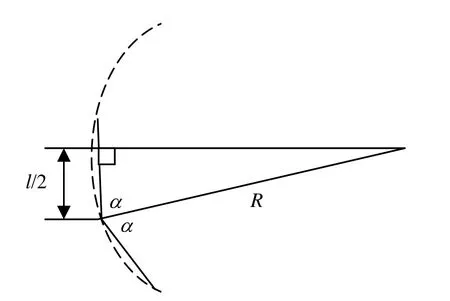
图2 曲线区段悬挂平面图

由结点各力对垂直轴和水平轴投影可得：

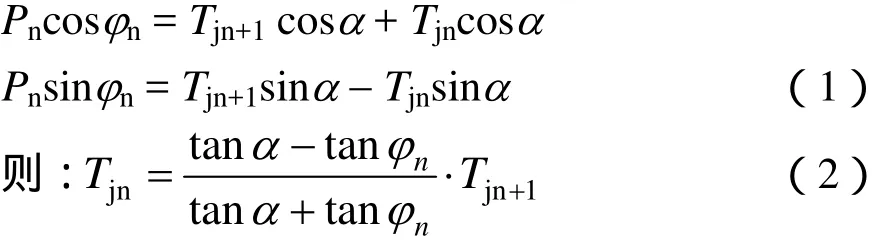
由图1和图2可知：

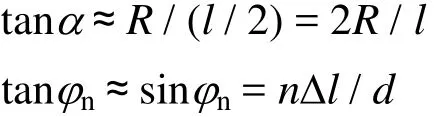
由中心锚结至补偿器间因定位器作用而形成的张力增量为Tj1－Tjm，即：

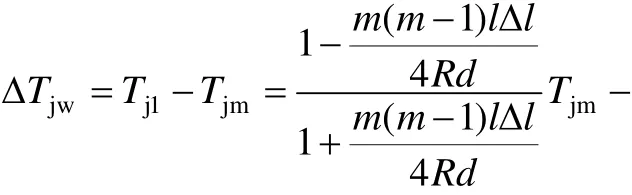
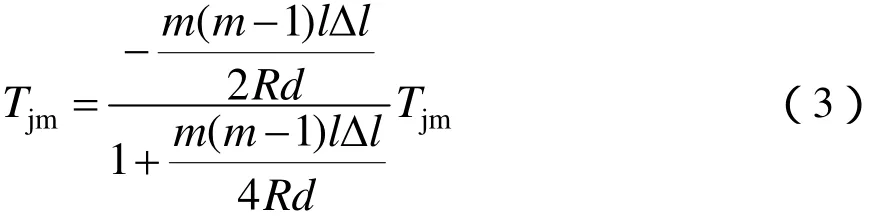
同前，将Δl = l(αΔl - ε)和 ml = L 代入上式，可得：

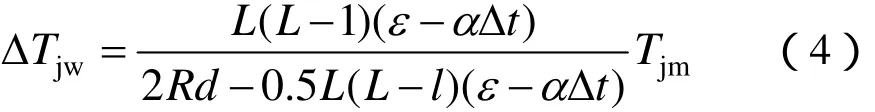
式中，Tjm为接触线在补偿处的张力，又称为起始张力。其定位器形成张力增量ΔTjw与起始张力Tjm成比例。造成张力变化的原因，实际上是由吊弦和定位器共同作用的。因此，起始张力中必须考虑吊弦的影响。而ΔTjd是一个抛物线，其平均张力增量为(2/3)(ΔTjd)，所以计算定位器造成接触线的张力差时，其起始张力应取：

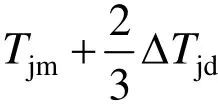
因而，由定位器的偏移对接触线所引起的张力增量为

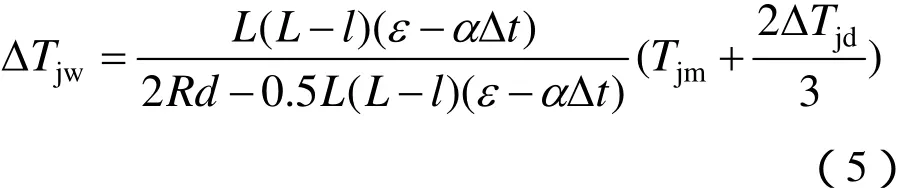
式（5）的应用条件为在曲线区段，且只考虑温度伸长和定位器偏移所引起的张力变化。在全补偿链形悬挂中，接触线弛度的变化更小，因温度变化而耗损于弛度变化方向的纵向位移也更小。故在计算中ε 可忽略不计，即令ε = 0。

3.2 吊弦造成的张力增量ΔTjd

现在先考虑在直线区段上，接触线由于温度变化而伸长，因吊弦偏移而造成接触线内的张力变化。为分析方便，先取出锚段中第n个支柱点来分析张力增量的形成（图3）。

在平均温度时，吊弦处在垂直位置。当温度变化后，由于接触线的伸长（或缩短），吊弦最低点的位置由A变到B。因为是半补偿，可以认为链形悬挂承力索不变，此时，接触线的受力情况要发生变化。因吊弦的倾斜产生了水平分量，即为张力增量，其值为

式中，m为半个锚段的跨距数；Δl为一个跨距内接触线的伸长，其值为

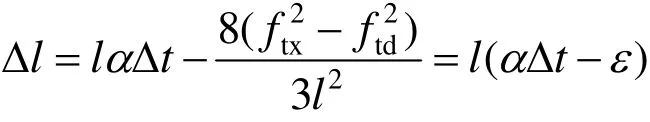
令ml = L，代入式（7）得：

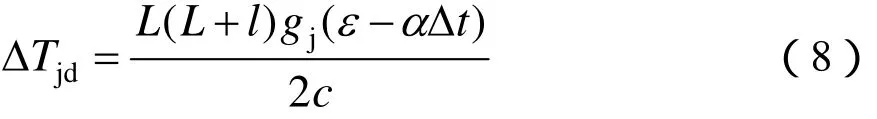
式中，ΔTjd为只考虑温度变化时，吊弦所引起的张力增量，kN；gj为接触线单位长度重量，kN/m；L为由中心锚结至补偿器间的距离，m；c为吊弦长度，取平均值，为最短吊弦，其值为cmin= h - F0。

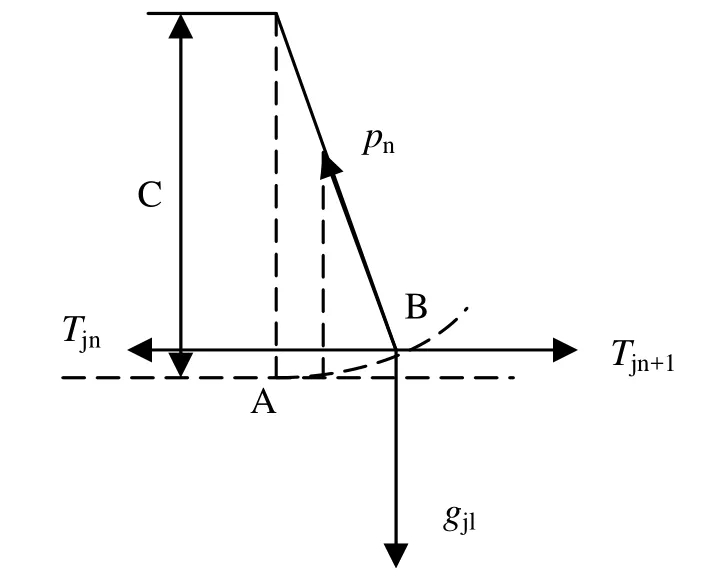
图3 吊弦的偏移示意图

式（8）的应用条件是在直线区段上；只考虑吊弦（Dx）所造成的张力变化和只考虑温度引起的伸长。

在全补偿链形悬挂中，接触线弛度的变化更小，因温度变化而耗损于弛度变化方向的纵向位移也更小。故在计算中ε 就忽略不计了，即令ε = 0。

3.3 中心锚结位置确定

在锚段长度和位置变化后，张力增量同样不应大于最大张力的10%，按照该条件，对变化后的锚段长度和线路情况按照式（5）、式（8）反求 L，即可求得中心锚结至补偿器间跨距数m。

4 算例

设悬挂形式为THJ-95+CTHA-120全补偿简单链形悬挂；承力索设计张力14.7 kN；接触线设计张力14.7 kN；承力索单位重量5.85 kN /m；接触悬挂单位重量16.93 kN /m，锚段长度1450 m，大部分位于曲线半径600 m位置，跨距45 m。

由式（5），α = 17.6×10-6K-1，Δt = 20℃，得：L = 493 m，则，m = 11跨。

由式（8），得：L = 402 m，则，m = 9跨。

由以上计算可得出，该锚段中心锚结位置应靠曲线方向距离张力补偿装置10跨。

5 结语

通过本文的讨论，对接触网锚段长度和线路情况变化后中心锚结位置的设置做了简单探讨，得出了相应计算式，从而减小了新设锚段内吊弦、腕臂等设备偏移量，并能够直接指导现场施工。希望本文能给遇到类似问题的工程技术人员提供帮助。

[1]于万聚.高速电气化铁路接触网[M].成都：西南交通大学出版社，2003.