基于非线性有限元法的海底管道剩余强度研究

,,,,

(1.中海石油(中国)有限公司天津分公司 天津，300452;2.中国石油大学(华东) 石油工程学院 山东 青岛，266580)

评估海底管道剩余强度的目的是为了研究在某一操作压力下是否允许缺陷存在，确定当前腐蚀缺陷下的最大允许工作压力及在某一工作压力下允许存在的最大腐蚀缺陷尺寸等，从而科学地指导管道的维修计划和安全生产管理，既保证海底管道运行的安全性，又保证了海底管道使用的经济性。

目前对于腐蚀管道压力计算准则有改进的ASME-B31G准则[1]、BATTLE准则[2]、DNV准则[3]及Shell-92准则[4]。这4种失效压力准则均采用了半经验的断裂力学的公式，没有考虑管道非线性的特点。在实际应用中，人们逐渐发现这些过分保守，它所预测的失效压力远远低于实际压力。这样的预测结果在工程使用上比较安全，但却造成了对管道不必要的维修或更换。由于承受载荷、工作环境和管道材料特性的影响，有些管道发生塑性变形，表现出几何非线性和材料非线性。在海底管道失效压力分析中，根据结构的特点和分析的需要，考虑几何非线性和材料非线性，可以得到更精确、更符合实际的结果。

1 非线性有限元法

1.1 材料模式

Waterloo大学通过几种典型材料的实验研究表明Ramberg．Osgood本构模型能较好地模拟海底钢管的非线性特征和管道屈服后的硬化性能[5]，而材料的硬化效应对管道的爆破失效影响很大。因此，计算模型中采用Ramberg-Osgood幂硬化应力-应变法则，其表达式为

(1)

式中：ε0——初始应变，ε0=σs/E;

σs——屈服应力;

E——弹性模量;

α——硬化系数;

n——幂硬化指数。

1.2 含缺陷管道失效的判定准则

在含缺陷管道的数值模拟中，对于爆破失效的判断提出了3种准则。

1)弹性极限准则[6]。只计算管道的弹性应力状态，即认为当腐蚀区的Mises应力不超过管材的屈服强度时，管道处于安全状态。该准则将管壁的应力完全限制在弹性范围内，比较保守。

2)基于塑性极限状态的失效准则[7]。腐蚀管道的失效可以由腐蚀区的环向应力值来确定，当环向应力值达到材料的抗拉强度时，管子发生塑性失效，否则就是安全的。该准则未考虑管道材料后屈服强化的影响，仍然有些保守。

3)基于塑性失效的准则[8]。当腐蚀区的应力状态达到材料后屈服终点时，即腐蚀区最小等效应力达到材料抗拉强度σb时，管道发生失效。

本文采用塑性极限状态的失效准则，即认为腐蚀区的最小等效应力达到材料抗拉强度σb时管线失效，此时所施加的荷载即为管线的失效压力。

2 力学模型简化

影响含腐蚀缺陷管道的极限荷载的因素有很多，也十分复杂。为了突出重点、抓住本质，在建立力学模型时，就要考虑结构特征、相关理论和工程实际经验等简化部分影响因素。下面是建立含腐蚀缺陷管道有限元力学模型的思路。

1)参数量纲一的量化。缺陷参数用相对长度l/D，相对深度d/t，相对环向角度θ/π来表征。其中：l是管道腐蚀长度；D是管道直径；d是管道腐蚀深度；t是管道壁厚；θ是管道腐蚀角度。

轴向位置用S/L表示，S是缺陷区域中心距管道一端的距离；L是管道长度。

2)缺陷位置的影响。由于海底管道是薄壳结构，内外腐蚀对管道强度的影响没有太大区别。实际上，海底管道在外表面是有混凝土保护层的，而内表面由于油气中的硫、硫化物以及细菌作用，腐蚀更严重一些。因此，在计算中采用内腐蚀缺陷为主。

3)缺陷形状规则化。现实中管道的腐蚀缺陷形状十分复杂，很难用几何模型真实描述，因此在建立有限元实体模型时，必须进行简化。考虑划分网格的困难，文中腐蚀形状用规则的弯曲长方形沟槽来模拟。

4)参数范围的选择。ASME中规定，当腐蚀最大深度小于壁厚的20%时，则含该缺陷的腐蚀区的管道仍可使用。当腐蚀最大深度大于壁厚的20%时，则含该缺陷的腐蚀区的管道必须更换或者修复。本文中的相对缺陷深度d/t分别为0.2、0.4、0.6、0.8；相对环向角度比θ/π分别为1/6、1/3、1/2、2/3；相对缺陷长度l/D分别为1∶2∶3∶4。

3 模型建立

为了减小模型规模，缩短计算时间，并且使内部缺陷可见，利用结构的对称，取模型的1/4进行分析，建立的模型见图1。

图1 管道腐蚀模型

根据Ramberg-Osgood幂硬化应力-应变法则，取硬化系数α=4、幂硬化指数n=5.4，由管道材料参数得出应力应变数据见表1、表2。

由于管道模型不规则，采用非结构化网格对管道模型进行网格划分；在缺陷处应力和应变变化梯度较大，分析的重点在缺陷部位以及缺陷的附近区域，因而在缺陷处的网格划分加密。为了节约计算成本，远离缺陷处选择比较稀疏的网格单元。 见图2。

表1 管道材料参数

表2 材料应力应变

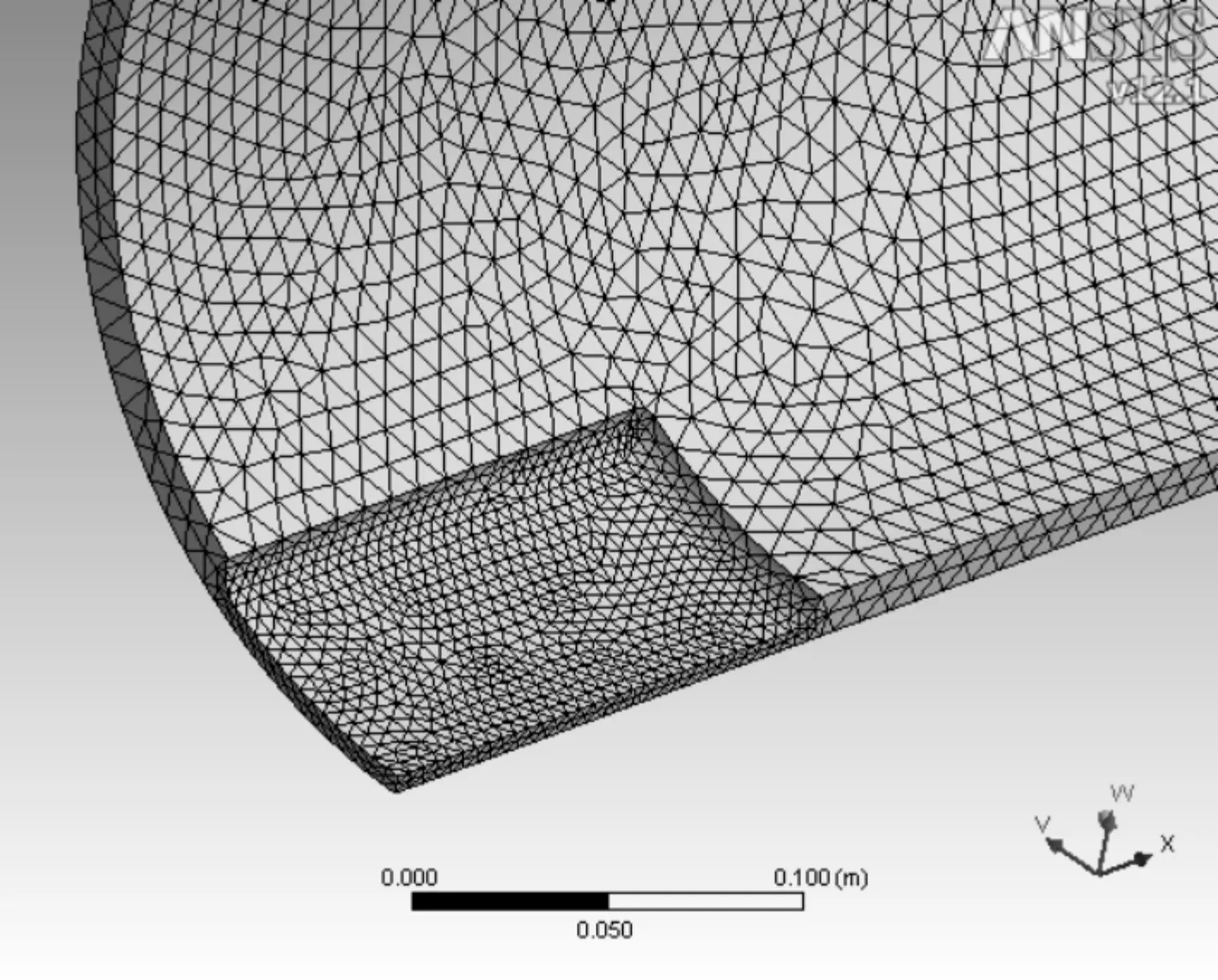
图2 腐蚀管道模型的网格划分示意

由于管道较长，而计算所取腐蚀区管段相对较短，因此可以不考虑管道的轴向位移；同时为计算收敛，直接在管道的一端取固定支撑，在管道对称面取对称支撑。

4 准则法与有限元法失效压力对比

本研究所取的海底管道参数外径为304.8 mm，壁厚为12.7 mm。表3为两种不同算法算得的不同腐蚀长度时的失效压力值。由表3可以得出：在相同腐蚀条件下，有限元算法的失效压力要比B31G算得的失效压力大15%～20%左右，但两种算法下，管道失效压力与腐蚀长度的变化关系曲线的趋势是相同的，失效压力随着腐蚀长度的增大都是先减小而后趋于平稳。

表4为两种不同算法算得的不同腐蚀深度时的失效压力。不同腐蚀深度下有限元算法与准则算法对比，在相同腐蚀条件下，在相对腐蚀深度小于等于0.6时，有限元算法的失效压力要比B31G算得的失效压力要大，但二值之差逐渐减小；在在相对腐蚀深度大于0.7时，有限元算法的失效压力要比B31G算得的失效压力小，且二者之差增大。两种算法的管道失效压力与腐蚀长度的变化关系曲线的趋势是相同的，失效压力随着腐蚀深度的增大而减小。

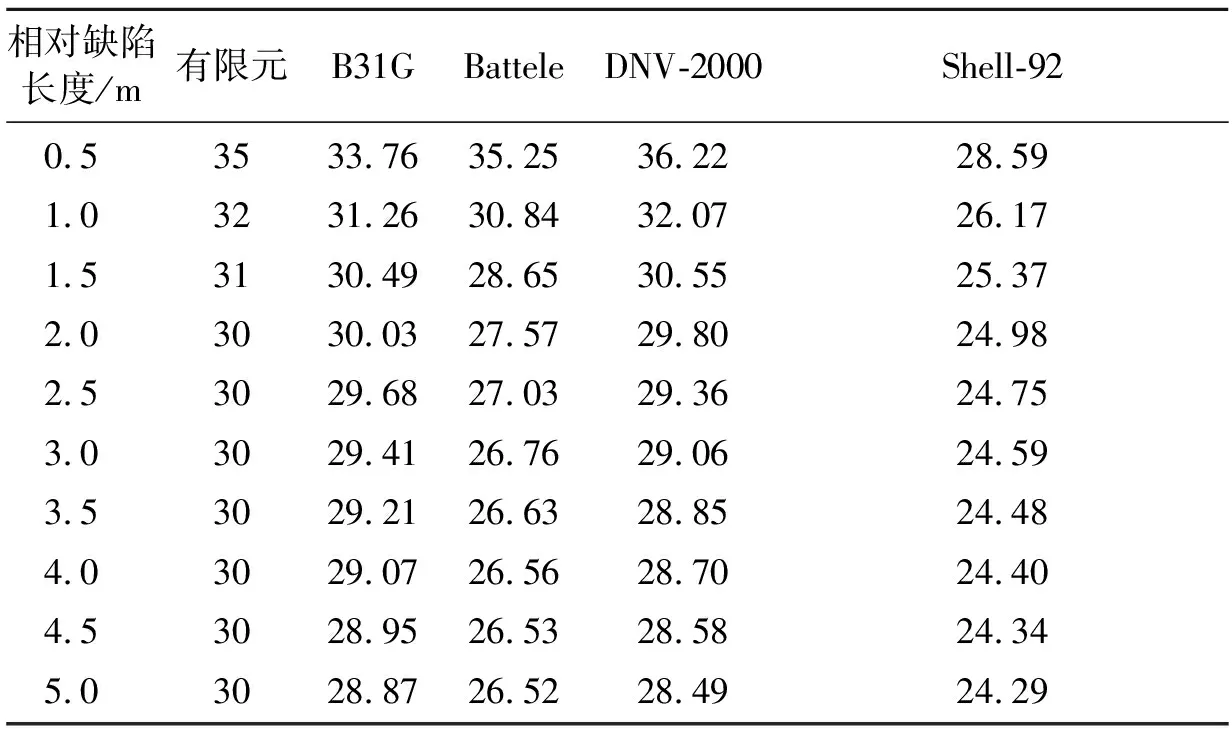
表3 两种不同算法算得的相对腐蚀长度的失效压力 MPa

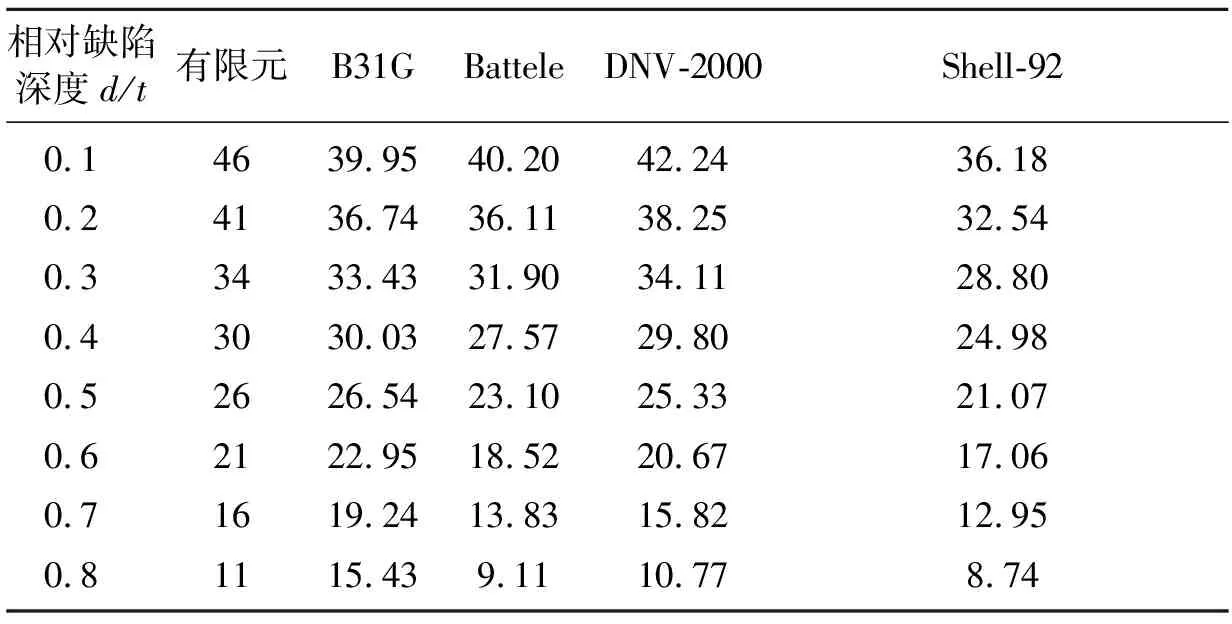
表4 两种不同算法算得的相对腐蚀深度的失效压力 MPa

5 影响因素分析

1)相对腐蚀深度对管道失效压力的影响规律。相对腐蚀长度l/D为2，腐蚀角度为30°，腐蚀位置为管道中心。图3为不同腐蚀深度下的失效压力，从图3可以看出：失效压力随着腐蚀深度的增大而减小。

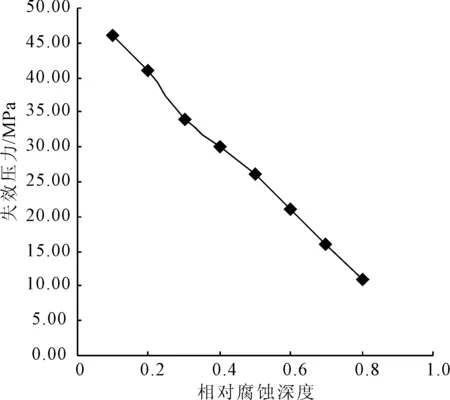
图3 相对腐蚀深度与失效压力变化曲线

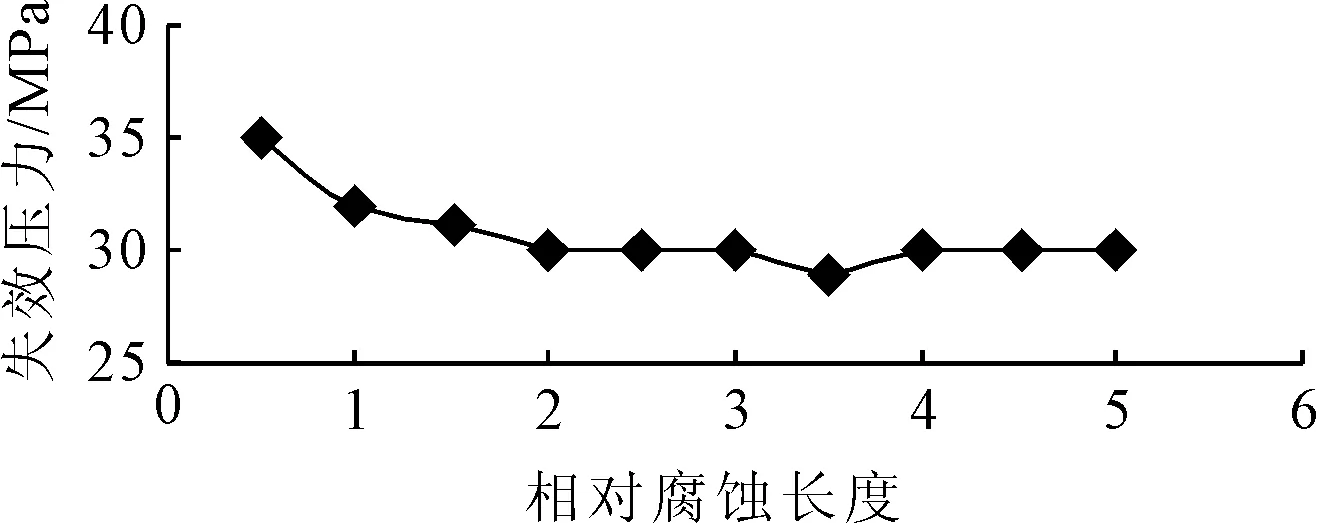
图4 相对腐蚀长度与失效压力变化曲线

2)相对腐蚀长度对管道失效压力的影响规律。相对腐蚀深度d/t为0.4，腐蚀角度为30°，腐蚀位置为管道中心。图4为管道在不同的腐蚀长度时的失效压力变化情况，可以看出失效压力随着腐蚀长度的增大先减小，而后趋于平稳。

3)腐蚀角度对管道失效压力的影响规律。相对腐蚀深度d/t为0.4，相对腐蚀长度l/D为2，腐蚀位置为管道中心。为了考察管道在不同的腐蚀角度时的失效压力变化情况，分别取腐蚀角度为15°，30°，45°，60°，75°，90°，105°，120°计算管道的失效压力，计算结果见图5。

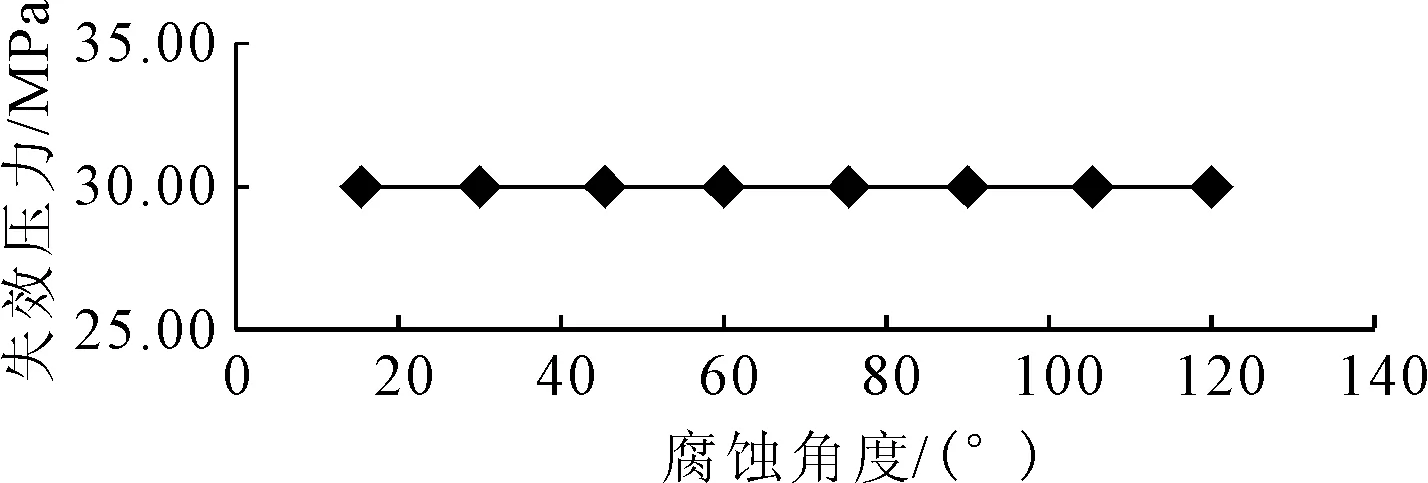
图5 腐蚀角度与失效压力变化曲线

由图5可见，腐蚀角度对失效压力影响不大。

4)轴向位置。由于需要考察腐蚀区域在悬空管道的轴向位置时管道的失效压力情况，腐蚀区域不全位于中心位置，所以1/4管道模型不再适合此次的强度分析，为此采用管道环向的1/2模型进行分析。为了考察存在腐蚀的悬空管道腐蚀区在不同的轴向位置时的等效应力变化情况，由于管道两端的支撑条件一样，所以只需计算腐蚀位置在距离任意一端时的管道等效应力情况即可，故分别取相对轴向位置S/L为1/20，2/20，3/20，4/20，5/20，6/20，7/20，8/20，9/20，10/20时的腐蚀区域，分别计算管道的失效压力，计算结果见图6，由此可见腐蚀轴向位置对失效压力影响不大。

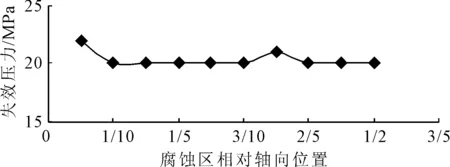
图6 失效压力随相对轴向位置变化曲线

5)环向位置。为了考察存在腐蚀的管道腐蚀区在不同的环向位置时的等效应力变化情况，分别取管道腐蚀区域中轴线与Y轴不同的夹角，其中腐蚀区域中轴线沿顺时针转动时为正，逆时针转动时为负，计算管道在不同腐蚀区中轴线与Y轴夹角时的等效应力，监测管道表面上的失效压力大小，计算结果见图7。由图7可见，随着腐蚀区域位置的变化，管道壁面上监测到的失效压力基本保持不变。

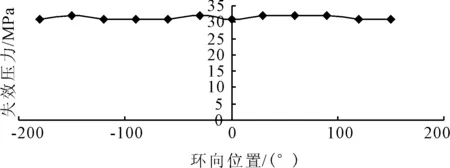
图7 失效压力随环向位置变化曲线

6 结论

1)非线性有限元法获得的腐蚀海底管道剩余压力与准则法相比，在相同腐蚀条件下，在相对腐蚀深度小于等于0.6时，有限元算法的失效压力要比准则法算得的失效压力要大，但二值之差逐渐减小；在相对腐蚀深度大于0.7时，有限元算法的失效压力要比B31G算得的失效压力要小，且二者之差增大。两种算法的管道失效压力与腐蚀长度、腐蚀深度的变化关系曲线的趋势是相同的。

2)非线性有限元法获得的失效压力随着腐蚀深度的增加而降低，随着腐蚀长度的增大先减小，而后趋于平稳，而对腐蚀角度和腐蚀位置的影响不敏感。

[1] ASME B31G.Manual for assessing remaining strength of corroded pipes[S].New York: American Society of Mechanical Engineers,2009,Pressure Vessels and Piping,2000, V123(3):561-565.

[2] LEIS N,STEPHENS D R.An alternative approach to assess the integrity of corroded linepipe[C].Part I current status and II alternative criterion,Proceedings of the Sev-enth International Offshore and Polar Engineering Conference,Honolulu, USA,1997:624-641.

[3] DNV-RP-F101.Corroded pipelines[S].Det Norske Veritas:Det Norske Veritas Elendom AS,2004.

[4] KLEVER F J,Stewart G.New developments in burst strength predictions for locally corrodes pipes[R].Houston:Shell Int Res,March 1995.

[5] HAUCH S,BAI KENNY J P.Use of finite element analysis for local buckling design of pipelines[C]∥Proceedings of Offshore Mechanic and Arctic engineering,1998．

[6] Wang Y S.A plastic limit criterion for the remaining strength of corroded pipe[C]∥Proceedings of the international Conference on Offshore Mechanics and Arctic Engineering(10th),Stavanger,Norway,June23-28,1991,Stavanger:ASME,1991.

[7] Hopkin P,Jones D G.A study of the behavior of long and complex-shape corroded in transmission pipelines[C]∥Proceedings of the 11th international Conference on Offshore Mechanics and Arctic Engineering,Calgary,Canada,June7-11,1992,Calgary:ASME,1992.

[8] Bin Fu.Advanced methods for integrity assessment on corroded pipelines[C]∥Proceedings of 1996 Pipeline Reliability Conference,Houston, USA,Nov.19-22, 1996,Houston:ASME,1996.