差分二次平均修正的频域相位补偿线谱检测方法
戴文舒,陈亚,陈新华,孙长瑜,余华兵
(1.中国科学院声学研究所,北京 100190;2.中国科学院大学,北京 100190;3.海军驻无锡地区军事代表室,江苏无锡 214061)
差分二次平均修正的频域相位补偿线谱检测方法
戴文舒1,2,陈亚3,陈新华1,孙长瑜1,余华兵1
(1.中国科学院声学研究所,北京 100190;2.中国科学院大学,北京 100190;3.海军驻无锡地区军事代表室,江苏无锡 214061)
针对常规平均功率谱方法幅度平方后相位信息丢失造成检测性能损失问题,通过对观测数据分段进行快速傅里叶变换后的统计特性进行分析,提出了高斯噪声背景下检测未知线谱的频域相位补偿方法。采用蒙特卡洛法估计相位补偿因子,先进行差分法去除零星野值,然后使用二次平均(TPM)去除连续野值,最后使用估计的相位补偿因子均值构造广义似然比检验统计量实现检测。从理论上对比了广义平均周期图(AVGPR)法、广义功率谱(GPR)法及文中方法的检测性能。仿真结果表明,文中方法充分利用信号的相位信息,参数估计简单,相位补偿因子估计准确,在一定虚警概率下较AVGPR法的检测性能提高了接近5 dB左右。
声学;快速傅里叶变换分析;线谱检测;频域相位补偿;检验统计量;功率谱
0 引言
Urick指出在一定假设下,海洋背景噪声服从高斯分布[1]。高斯背景下未知线谱的检测近年来一直被关注,随着隐身技术的不断提高,水下目标辐射线谱信号越安静,对被动声纳的检测性能要求越苛刻。功率谱分析与低频分析和记录(LOFAR)结合来检测线谱是使用最普遍的方法,然而该方法的检测模型中功率谱的计算只用到了线谱信号的幅度信息,相位信息在平方观测值的离散傅里叶变换(DFT)后丢失。相位信息的丢失会降低被动声纳检测的性能。针对相位信息的补偿,国内外的相关学者进行了一系列研究,大多从时域平均角度出发。沈国际等指出当信号频率未知或由采样频率的关系无法实现对信号的整数倍周期截取,会导致性能大大下降,甚至反而降低信噪比[2]。陈绍华等提出在频率已知的条件下,对每段截取信号进行时延补偿,从而得到无相位误差的时域平均方法[3]。而对于频域未知的情况,则补偿时需要进行频率搜索,计算量大,为此,陈新华等提出了搜索频率与信号频率无关,仅是截取长度倒数的方法,大大减小了计算量,根据不同的搜索频率对每段截取信号进行相位补偿,使时域平均后的输出功率到达最大[4]。Chun等提出的最优线谱广义似然比检测(PGLRT)改进了广义平均周期图(AVGPR)的幅度功率谱检测缺陷,充分利用了功率谱的分布特性,但是其检验统计量的估计值参数遇到了低信噪比时的虚数解,导致检测结果发散[5]。
本文从频域功率谱角度出发,先对二元统计模型下功率谱分布特性进行分析,然后研究分段快速傅里叶变换(FFT)后相位因子的存在带来的影响及补偿方法及估计方法,进而使用估计得到的相位影响因子使用最大似然准则构造检验统计量,从模型出发理论分析AVGPR、广义功率谱(GPR)及本文方法的检测性能,最后给出了算法的仿真结果和主要结论。
1 检测问题和模型
检测问题可以描述为二元假设检验,

式中:s(n)=Aexp(j(w0n+φ))是待检测信号,A是信号的未知幅度,w0是未知归一化角频率,φ∈(0, 2π)是初始化相位,未知但是固定;g(n)是方差为的高斯噪声。将x(n)分成长度为N的L段,总长度为Q,R与重叠个数有关,第l段表示为

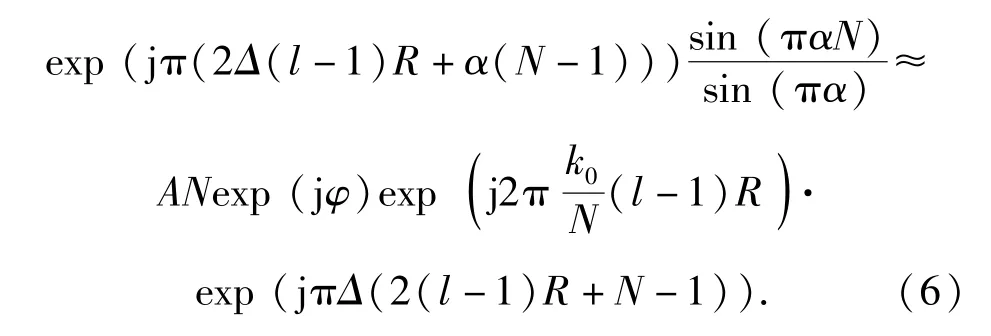

上式表明在最接近信号的数字频率单元观测值的功率将最大。由于信号频率未知,需要通过搜索来确定频率单元。这显然计算量大,不可取。
记信号部分为ρl(k),可以看出Δ的存在带来的相移,所以需要进行补偿修正。
对于噪声频率单元,k≠k0,信号成分很小, Zl(k)服从0均值、方差σ2的高斯分布;对信号频率单元Zl(k)服从μl均值、方差σ2的高斯分布,其中
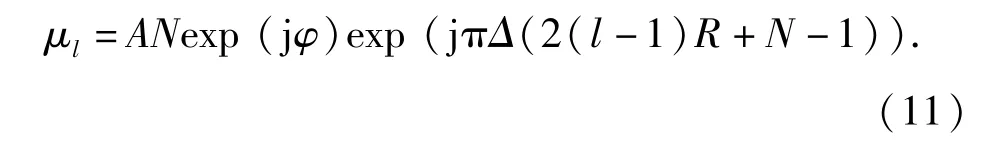
为使用相位信息,Δ的估计很重要,从(11)式看到,Δ与2Δ((l-1)R+N-1)相乘,每段的相移不同,为了充分利用各段的相位信息,由Δ引起的相移需要补偿。
2 Δ因子的估计
补偿相移的关键是对Δ因子进行估计。文献[5]中指出了用解非线性方程的方法估计Δ,涉及多解问题和初始化猜想。而通过对Zl(k)进行L点DFT分析:


3 差分二次平均方法去野值
由中心极限定理,满足任何分布的P个独立观测值的均值服从正态分布[7],所以采用蒙特卡洛仿真500次,由仿真结果^Δ的估值会出现野值。为了得到准确的估计结果,要先对这些数据进行预处理。
根据存在野值的特点分为零星野值和连续野值,它们的存在会使得^Δ的均值的估计值偏离真实值,所以要进行判断和去除。零星野值点与它左右领域点的差值都很大,如图1中第i次估计;若待研究点与其左右领域点的差值只有一个很大,那么既可以是野值点,也可以是临界点,如图1中第i-1次估计。
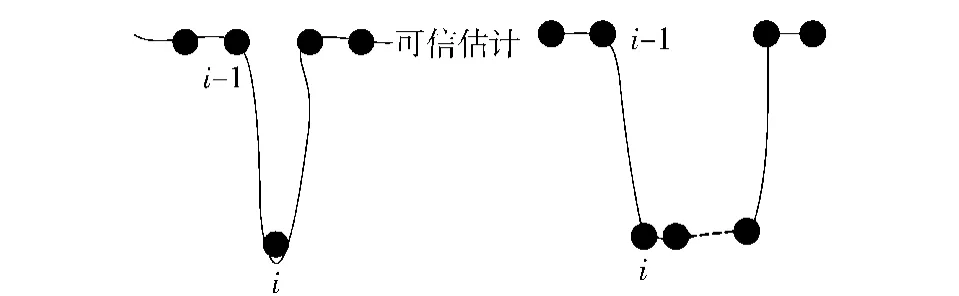
图1 零星野值和连续野值Fig.1 Sporadic and continuous outliers
文献[8]比较了估计背景均值的4种方法。本文采用广泛使用的二次平均(TPM)估计均值,再根据莱特准则去除连续野值。下面方法描述TPM技术,μk是第k个单元的估计均值,它是其领域Ωk输出的函数,位于中心,K=2M+1窗长。

可见μk是一系列值,计算μk的均值μ和方差σ2.采用莱斯准则判断去零星野值后的3σ,则去除该点。最后用剩余的可信估计来估计Δ.
4 由估计值^Δ补偿各段相移
由(10)式看到在(9)式两边乘以因子exp(-jπ· Δ(2(l-1)R+N-1))来补偿每段的相移得到Yl(k),其表达式如(20)式。

在两种假设下的联合概率密度函数(PDF)分别为

式中:未知参数为A、σ2.构造对数似然比

在假设H0下,未知参数为σ2,最大似然估计^σ20可由(24)式得到。

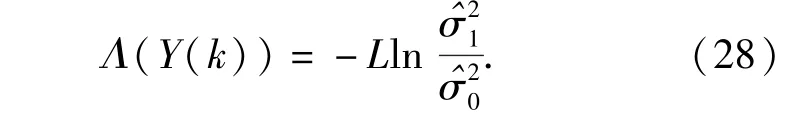
综上,基于差分TPM修正的频域相位补偿算法流程图如图2所示。
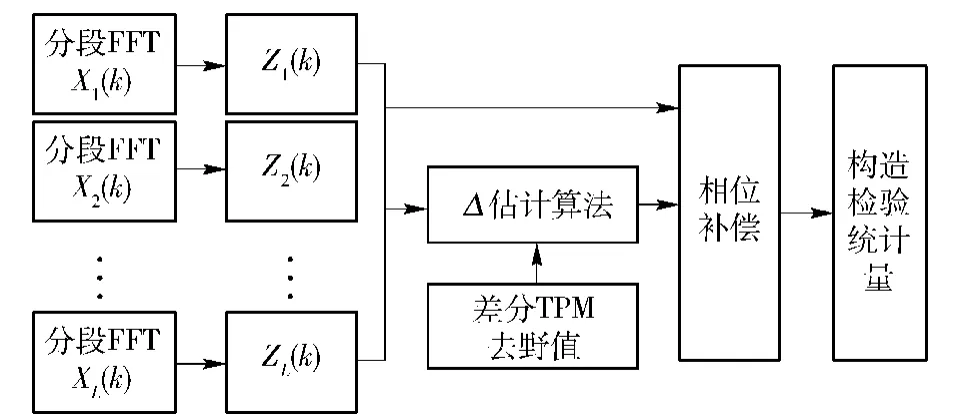
图2 基于差分TPM修正的频域相位补偿流程图Fig.2 Flow chart of frequency domain phase compensation using difference and TPM
5 性能分析
文献[9]分析了平均周期图法的检测性能。以下列出主要公式:


Matlab工具箱中提供了计算这些概率值的函数,仿真可直接调用。
6 仿真性能曲线
分别根据(36)式、(42)式画出AVGPR、本文方法的受制者工作特性(ROC)检测性能曲线,GPR是自由度为2的AVGPR.本文方法记作RGLRT.图3表示信噪比为-25 dB、L=32下的理论ROC曲线。图4表示信噪比为-30 dB下的理论ROC曲线。图5为虚警概率PFA=10-3下的检测概率PD随信噪比SNA的变化规律。
理论分析RGLRT算法比AVGPR算法在PFA= 10-3下检测性能增加了提高了近5 dB左右。而众所周知,AVGPR算法相比GPR算法的性能提高是由分段累积带来的。
7 仿真验证

图3 信噪比为-25 dB下的ROC性能曲线Fig.3 Detection performance for SNR=-25 dB
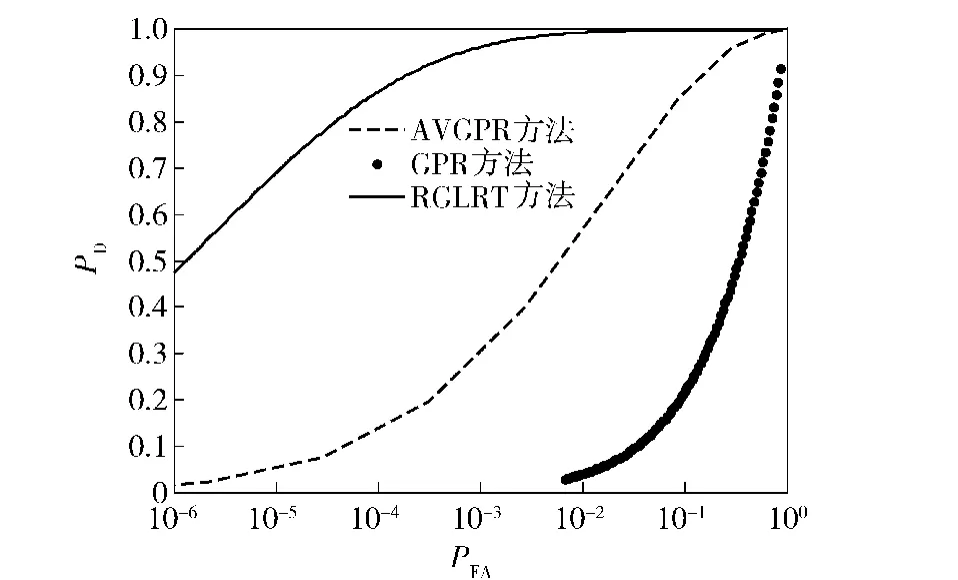
图4 信噪比为-30 dB下的ROC性能曲线Fig.4 Detection performance for SNR=-30 dB
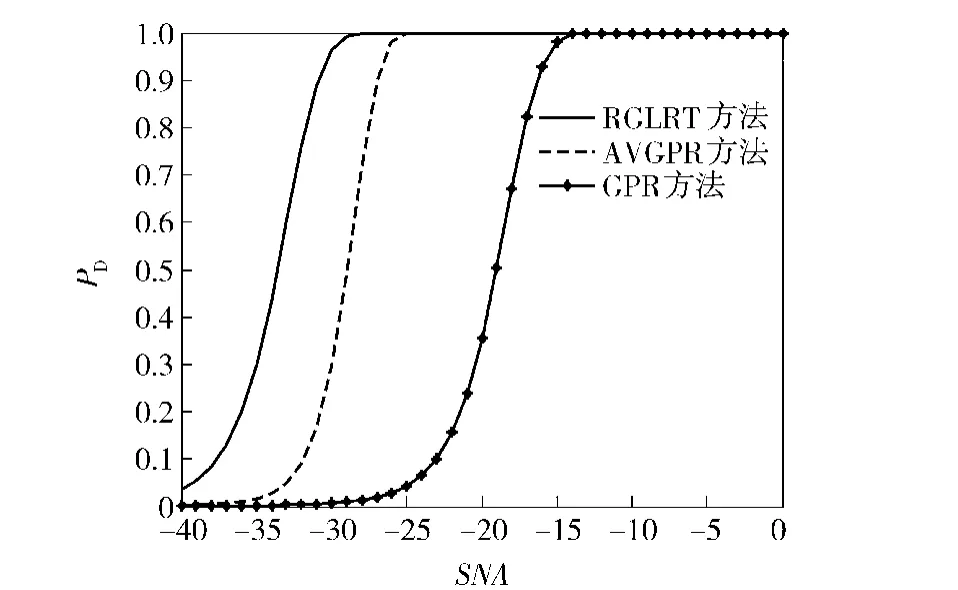
图5 虚警概率一定下的ROC性能曲线Fig.5 Detection performance at a certain false alarm rate
1)仿真条件:采样频率fs=512 Hz,观测总数Q=20 000,分段数L=39,每段长度512,蒙特卡罗仿真次数P=500,取TPM窗长度K=3,信噪比-29 dB.仿真信号频率变化,对比了真实Δ与去野值前后估计值的结果。
由表1可知,未去野值时^Δ的估计均值较去野值后的^Δ的估计均值与真实Δ的误差较大,会导致各段相位补偿的不准确,影响检测性能,而且未去野值的的估计方差要比去野值后的大。差分TPM提高了相移估计因子的估计准确性。
表1 信噪比-29 dB下估计均值和真实值Δ的仿真结果Tab.1 The simulation results of estimated and true values for SNR=-29 dB
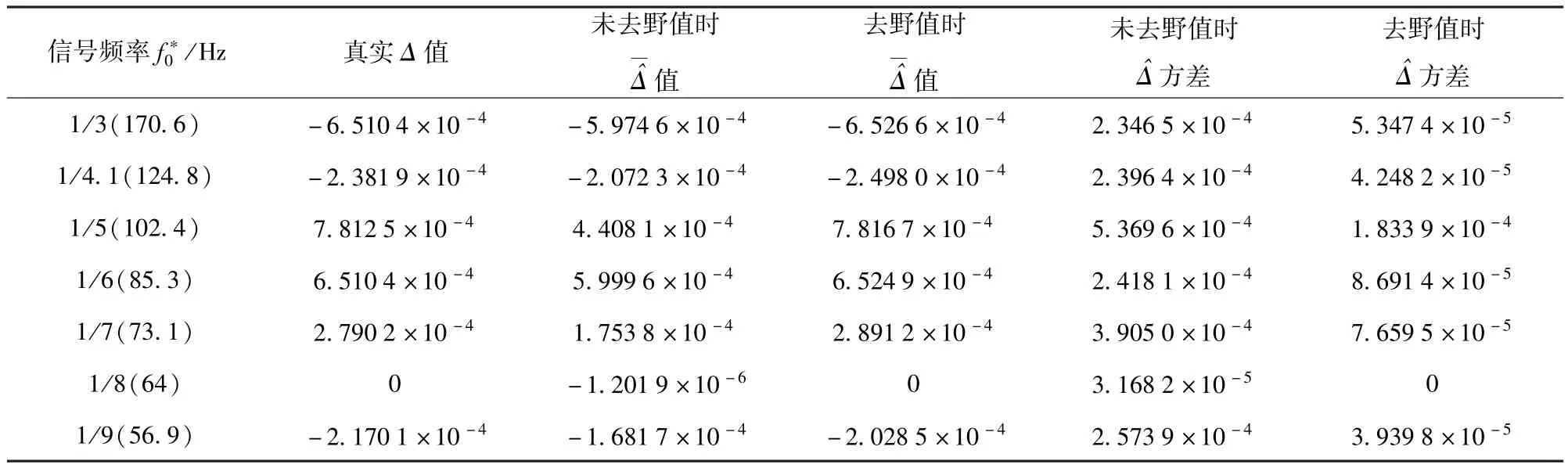
表1 信噪比-29 dB下估计均值和真实值Δ的仿真结果Tab.1 The simulation results of estimated and true values for SNR=-29 dB
信号频率f*0/Hz真实Δ值方差1/3(170.6)-6.510 4×10-4-5.974 6×10-4-6.526 6×10-42.346 5×10-45.347 4×10未去野值时^Δ值去野值时^Δ值未去野值时^Δ方差去野值时^Δ -5 1/4.1(124.8)-2.381 9×10-4-2.072 3×10-4-2.498 0×10-42.396 4×10-44.248 2×10-51/5(102.4)7.812 5×10-44.408 1×10-47.816 7×10-45.369 6×10-41.833 9×10-41/6(85.3)6.510 4×10-45.999 6×10-46.524 9×10-42.418 1×10-48.691 4×10-51/7(73.1)2.790 2×10-41.753 8×10-42.891 2×10-43.905 0×10-47.659 5×10-51/8(64)0-1.201 9×10-603.168 2×10-50 1/9(56.9)-2.170 1×10-4-1.681 7×10-4-2.028 5×10-42.573 9×10-43.939 8×10-5
由第3节信噪比-30 dB下的ROC理论分析可知,在虚警概率PFA=10-3下AVGPR算法的检测概率为0.3,而RGLRT算法的检测概率为1,PGLRT算法不能实现检测。
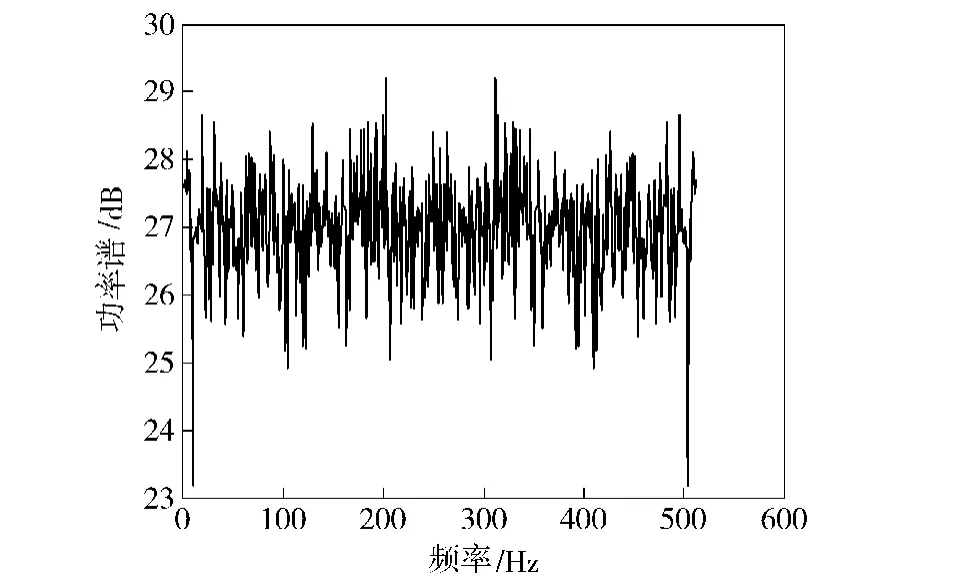
图6 AVGPR算法下的检测结果Fig.6 Detected result of AVGPR algorithm
8 结论
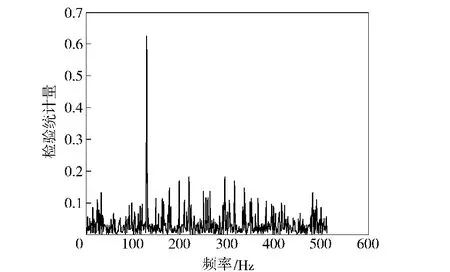
图7 RGLRT算法下的检测结果Fig.7 Detected result of RGLRT algorithm
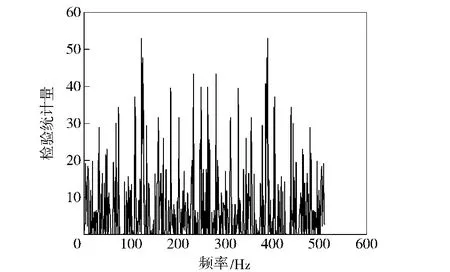
图8 PGLRT算法下的检测结果Fig.8 Detected result of PGLRT algorithm
1)对观测数据分段进行FFT后的功率谱二元统计模型及分布进行研究,得出了各段的AVGPR在没有线谱信号时服从自由度为2L的中心chi平方分布,而线谱存在时服从自由度为2L的非中心chi平方分布,非中心参数为λ=N本文基于频域相位补偿的似然比检测统计量在没有线谱存在时服从中心F分布,在线谱存在时服从非中心F分布,非中心参数为λ=NGPR是自由度为2的AVGPR.
2)相同分段数下,理论分析本文算法比AVGPR算法在PFA=10-3下检测性能提高了近5 dB左右,而且F分布较chi平方分布在达到同样检测概率时的检测门限低,所以性能更优。
3)基于前后向差分去除零星野值后采用TPM估计均值方法,有效地去除了连续野值,提高了相位影响因子的估计准确性,提高了检测统计量的检测性能。
(References)
[1] Urick R J.Models for the amplitude of fluctuations of narrow-band signals and noise in the sea[J].J Acoustic Soc Amer,1977,62: 878-887.
[2] 沈国际,陶利民,徐永成.时域同步平均的相位误差累积效益研究[J].振动工程学报,2007,20(4):335-339.
SHEN Guo-ji,TAO Li-min,XU Yong-cheng.Research on phase error accumulation effect of time synchronous averaging[J].Journal of Detection and Control,2007,20(4):335-339.(in Chinese)
[3] 陈绍华,相敬林.一种改进的时域平均法检测微弱信号研究[J].探测与控制学报,2003,25(4):56-59.
CHEN Shao-hua,XIANG Jing-lin.Amodified time averaging method in weak signal detection[J].Journal of Detection and Control,2003,25(4):56-59.(in Chinese)
[4] 陈新华,孙长瑜,鲍习中.基于相位补偿的时域平均方法[J].应用声学,2011,30(4):268-274.
CHEN Xin-hua,SUN Chang-yu,BAO Xi-zhong.Time domain averaging based on phase compensations[J].Applied Acoustics, 2011,30(4):268-274.(in Chinese)
[5] Chun R W,Joo T G,Hong T C.Optimaltonal detectors based on the power spectrum[J].IEEE Journal of Oceanic Engineering, 2000,25(4):540-552.
[6] Qing W,Chun R W.Anovel CFAR tonal detector using phase compensation[J].IEEE Journal of Oceanic Engineering,2005, 30(4):900-911.
[7] 施久玉.概率论和数理统计[M].哈尔滨:哈尔滨工程大学出版社,2005.
SHI Jiu-yu.Probability andmathematics[M].Harbin:Harbin Engineering University Press,2005.(in Chinese)
[8] Willan A S,Edward D L.A performace comparison of four noise background normalization schemes proposed for signal detection systems[J].J Acoustic Soc Amer,1984.76(6):1738-1742.
[9] Qing W,Chun W,Joo T G.Theoretical performance analysis and simulation of a GLRT tonal detector[C]∥Oceans 2001 MTS/ IEEE ConfErence and Exhibition.Honolulu,HI:IEEE,2001: 1654-1659.
[10] Kay S M.统计信号处理基础:估计与检测理论[M].罗鹏飞,译.北京:电子工业出版社,2001.
Kay S M.Fundamentals of statistical signal processing:estimation theory and detection theory[M].LUO Peng-fei,translated. Beijing:Publishing House of Electronics Industry,2001.(in Chinese)
An Algorithm of Line-spectrum Detection Using Frequency Domain Phase Compensation with Difference and TPM Technique
DAI Wen-shu1,2,CHEN Ya3,CHEN Xin-hua1,SUN Chang-yu1,YU Hua-bing1
(1.Institute of Acoustics,Chinese Academy of Sciences,Beijing 100190,China; 2.University of Chinese Academy of Sciences,Beijing 100190,China; 3.Navy Military Representative Office in Wuxi Area,Wuxi 214061,Jiangsu,China)
The common average power spectrum estimation algorithm may cause the loss in detection performance because power spectrum amplitude is simply squared.The statistical properties of FFT of the segmented observations are analyzed,and a novel algorithm using frequency domain phase compensation for detecting line-spectrum in Gaussian noise is proposed.The phase compensation factor is estimated using Monte Carlo method.The sporadic and continuous outliers are removed by using difference and TPM method.Finally the statistics is checked by using generalized likelihood ratio.The detection performances of AVGPR,GPR and the proposed algorithm are theoretically compared.The simulation results show that the detection performance of the proposed algorithm is improved by 5 dB under a certain false alarm rate compared to AVGPR algorithm.It fully utilizes the phase information of the signal and has the advantagesof simple and exact parameter estimation and good robustness.
acoustics;FFT analysis;line-spectrum detection;frequency domain phase compensation; test statistics;power spectrum
TB566
A
1000-1093(2014)10-1630-08
10.3969/j.issn.1000-1093.2014.10.017
2013-08-06
国家自然科学基金项目(61372180)
戴文舒(1987—),女,博士研究生。E-mail:dws.01@163.com;陈亚(1978—),男,工程师。E-mail:cheya113@sina.com

