基于K近邻非线性分类器的高光谱遥感数据分类研究

莫文通,周 源

(1.南宁市勘察测绘地理信息院,广西南宁 530022; 2.同济大学测绘与地理信息学院,上海 200092)

基于K近邻非线性分类器的高光谱遥感数据分类研究

莫文通1∗,周 源2

(1.南宁市勘察测绘地理信息院,广西南宁 530022; 2.同济大学测绘与地理信息学院,上海 200092)

K近邻等传统分类算法在高光谱遥感影像数据上进行分类时,由于其高维度、非线性特点,分类效果会受到严重影响。本文利用核函数方法,融合K近邻分类算法与Isomap非线性降维算法,提出了一种新的K近邻非线性分类器。该分类器无需通过降维预处理,并具备处理非线性数据的能力。在实验中,通过交叉验证与参数验证证明该方法在高光谱遥感影像上的分类效果明显优于原始K近邻分类算法以及结合主成分分析法的K近邻分类法。

高光谱遥感;分类算法;K近邻算法;非线性分类器

1 引 言

K近邻分类算法[1]是利用遥感影像进行土地利用/土地覆盖调查最常用的传统分类方法之一。该算法模型简单、直观、易于实现和操作。目前,绝大多数遥感应用软件如ERDAS、ENVI等都植入了该算法作为遥感分类的默认算法。由于该方法仅依靠有限的近邻样本确定待定样本的类别,因此对于类间的交叉和重叠较为严重的待定样本,K近邻算法能获得更好的分类效果。随着高光谱遥感数据在土地利用/土地覆盖应用中的广泛普及,其高维度、非线性特征等特点会严重影响传统分类算法,尤其是K近邻算法的分类效果[2]。

为了解决这一问题,在进行分类前通常会使用降维方法降低遥感数据的维度。但传统的降维方法如主成分分析法(PCA)、最小噪声分离法(MNF)等缺乏提取非线性特征的能力。近年来,涌现了一批以Isomap算法为代表的基于流形的非线性降维方法[3,4],它们在降低观测数据空间维度的同时可从观测空间中提取嵌入在该空间的非线性特征。该类新方法在遥感数据处理中已取得许多成功的应用[5,6]。但是,该类方法需要显式计算出观测数据降维后对应的低维坐标,使得降维过程计算复杂度过高。当观测数据量增加时,该类算法降维时消耗的计算时间会显著增加。

因此,本文利用核函数方法[7],提出了一种将Isomap算法与K近邻算法相融合的K近邻非线性分类器。在使用该分类器时,无需显式计算观测数据的低维非线性表达,只需利用Isomap算法的核函数直接将观测数据的非线性信息带入到K近邻算法中进行分类。这种做法的优点是一方面避免了显式降维计算,节约大量计算资源;另一方面仍然能有效提高原始K近邻算法在高光谱遥感影像上的分类精度。

2 研究方法

2.1 K近邻分类算法

K近邻分类算法简单、直观。使用该算法将D维空间观测数据集X=[x1,…,xN](N为数据数量)分为C个类别的过程如下。首先,记录训练样本数据集Y= [y1,…,yM](M为训练样本数量)以及每个训练样本数据对应的类别标记∈[1,…,C](为第j个训练样本数据的类别标记)。其次,定义该观测空间度量d(x,y),通常的选择包括欧氏距离、角距离、马氏距离等。在明确度量的前提下,获取数据集中任意观测数据点xi在训练样本数据集Y中的k个近邻:Yi=[ynn1,…,ynnk],{ynn1,…,ynnk∈Y}。最后,依照多数投票法则,可通过Yi中数据点对应的类别得到观测数据点xi所属类别:

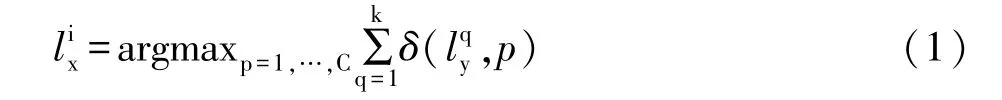
2.2 Isomap非线性特征提取方法

Isomap是一种基于等角映射的非线性降维方法。在使用分类器前使用Isomap方法对观测空间中的数据集进行降维,不仅能解决观测数据高维度造成的分类器计算复杂度过高的问题,还能提升分类器处理非线性分布数据的能力。

通常高维观测空间的数据分布具有较强的稀疏性,这些观测数据可本看做分布在一个嵌入在高维观测空间中的低维流形上。Isomap方法利用最短路径搜索和多维排列法得到观测数据在这个嵌入流形上的测地线距离关系,并通过该非线性关系将观测数据投影到一个低维空间中,从而得到原始高维空间中数据集的非线性特征。其具体算法可见表1,有关该方法的证明可参考[8]。

表1 Isomap算法实现流程

2.3 基于Isomap的K近邻算法核函数化

在Isomap方法提取的低维非线性特征空间的基础上使用K近邻方法分类可提升其对非线性分布数据的分类能力。但是随着观测空间数据量的增加,对数据点进行一一显式空间变换的计算复杂度会越来越高。并且显式空间变换的解算过程会数据信息丢失和精度降低。为了解决以上问题,本文提出采用核方法将Isomap空间变换的核函数结合到K近邻分类算法中,从而采用隐式空间变换的方法,省略计算空间变化结果的步骤,让结合核函数的K近邻算法直接在观测空间中对数据进行分类。

核方法的原理如下:遵循Mercer定理。令Φ为D维特征空间S1到d维特征空间S2的映射:

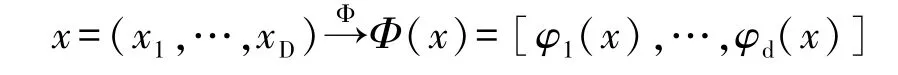
其中,x∈S1,Φ(x)∈S2。则对于x,y∈S1,有核函数K:K(x,y)=＜Φ(x),Φ(y)＞

＜∵＞为内积符号。

由于核函数K(x,y)的计算复杂度远小于分别计算x,y在S2中的像以及像间内积过程。因此在分类器模型中通常使用核函数替代原有观测数据点的内积,从而降低空间变换的计算代价,增强模型对非线性数据的处理能力。该方法已广泛应用于如支持向量机、簇分析、数据降维等应用中。

在K近邻分类算法模型式(1)中虽然没有可直接转化核函数的内积式,但是由于寻找K近邻需要使用度量关系式(2),利用该式可实现K近邻分类算法的核函数化:

根据式(2)可得到空间变化后数据点间的距离度量:

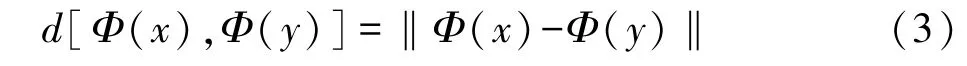
将式(3)的平方形式d2[Φ(x),Φ(y)]展开易得其内积的表达形式:

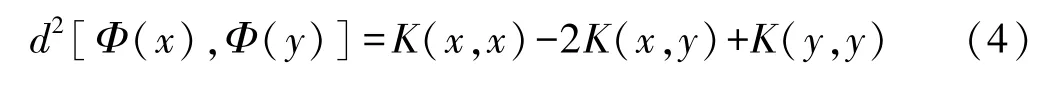
根据式(4)即可求解数据点在核函数K对应空间中的距离关系,进而得到其在该空间中的近邻,从而实现在变换空间中的K近邻分类算法。

根据Nystrom定理[9],易知Isomap方法的核函数为:

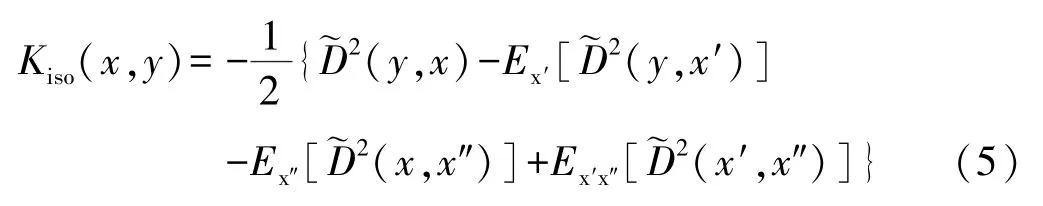
Kiso(x,y)为观测空间中任意数据点x与训练样本中任意数据点y的核函数,右式中x′、x″为训练样本中的任意数据点点,~D(∵)为两点间测地线距离,E[~D2(x,·)]是x点与训练样本集合中数据点测地线距离的期望值。将式(5)带入式(4)中,即可利用核函数使K近邻分类算法在Isomap模型提取的非线性信息的基础上进行分类计算。

3 实验结果与分析

本实验选用了国际通用的标准高光谱遥感数据集Indian Pine以检验新算法的分类效果。该数据集由AVIRIS机载传感器获取,空间分辨率为30 m,有效光谱范围覆盖400 nm～2 500 nm波段范围共220个波段,经过剔除噪声波段与水汽吸收带,保留158个波段。该数据集影像大小为145×145像素,依据地面实况数据可分为12个类别(表2)。数据集的假彩色影像以及地面实况数据的分布情况如图1所示。

表2 实验数据地物类别与分布情况

图1 影像数据实验对比图

为了验证基于Isomap的核函数化K近邻分类算法的分类性能,本文采用交叉验证的方法对比原始K近邻算法、采用PCA算法的K近邻算法和本文提出的K近邻算法的分类精度。在交叉验证过程中,地面实况数据被随机平均分为一百份进行一百次分类计算。测试时,将每份子集作为训练样本,其余数据作为测试样本进行一次分类,得到当次的分类精度。实验的最终分类精度为一百次分类的平均精度。在分类过程中,三种算法的模型参数设置为:K近邻数量为3个,训练样本数量为100个像素,分类结果如图2所示。其中,原始K近邻模型的分类精度为54.76%± 1.85%;在使用PCA降维到10个维度上使用K近邻分类算法的分类精度为54.63%±1.85%;采用本文提出的非线性K近邻分类方法的分类精度为60.9%± 1.99%。与原始K近邻分类算法相比,新算法的分类精度提高了11.21%;与基于PCA的K近邻分类算法相比,新算法的分类精度提高了11.48%。

在以上实验中,在算法输入参数一致的情况下,新算法在分类精度上与原始K近邻算法相比有较为明显的提高。为了进一步验证新分类算法的稳定性,实验将分别逐渐增加训练样本数量与K近邻数量,在改变参数的过程中比较三种分类算法的分类精度及其变化。

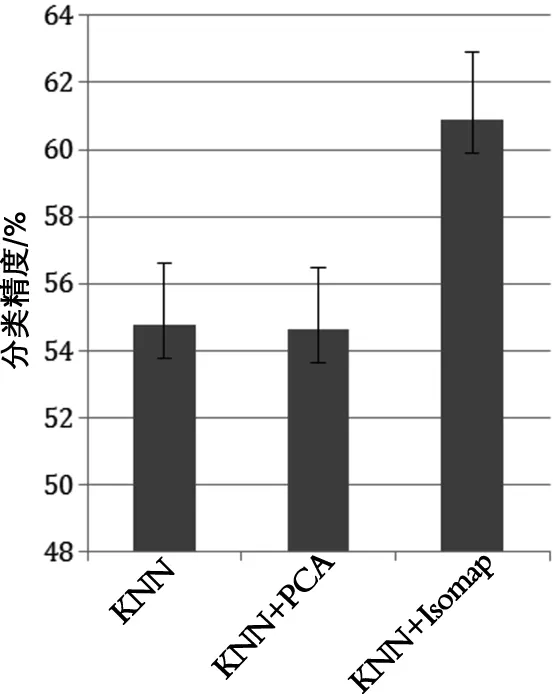
图2 原始K近邻算法、PCA结合K近邻算法与本文算法分类精度对比图

其中,图3为K近邻数量为3个,训练样本数量由100像素增加至500像素时,三种分类算法的分类精度变化结果。由该图可见,随着训练样本数量的增加,三种算法的分类精度都逐渐提高;但是新算法的分类精度始终高于其他两种算法。其中,当训练样本数量为100个像素时,与原始K近邻算法和基于PCA的K近邻算法相比新算法分别将分类精度提高11.21%与11.48%;当训练样本数量为200个像素时,新算法分别将分类精度提高9.10%与9.43%;当训练样本数量为300个像素时,新算法分别将分类精度提高8.92%与8.82%;当训练样本数量为400个像素时,新算法分别将分类精度提高7.29%与7.82%;当训练样本数量为500个像素时,新算法分别将分类精度提高7.42%与7.97%。

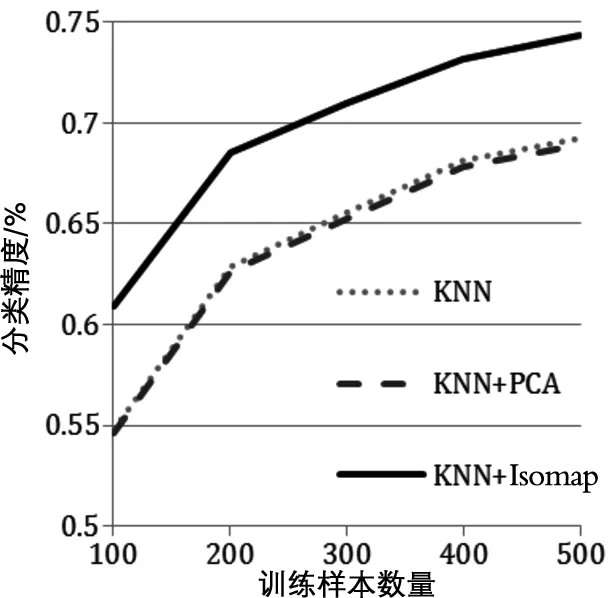
图3 随训练样本数量增加时各分类方法的分类精度变化图

图4 为训练样本数量为500个像素,K近邻数量由3个增加至9个时,三种分类算法的分类精度变化结果。由该图可见,随着K近邻数量的增加,三种算法的分类精度都逐渐降低;但新算法的分类精度仍然高于其他两类算法。其中,当K近邻数量为3个时,与原始K近邻算法以及基于PCA的K近邻算法相比,新算法分别将分类精度提高7.42%与7.97%;当K近邻数量为4个时,新算法分别将分类精度提高7.30%与7.78%;当K近邻数量为5个时,新算法分别将分类精度提高7.06%与7.48%;当K近邻数量为6个时,新算法分别将分类精度提高7.57%与8.10%;当K近邻数量为7个时,新算法分别将分类精度提高7.37%与7.79%;当K近邻数量为8个时,新算法分别将分类精度提高7.69%与8.00%;当K近邻数量为9个时,新算法分别将分类精度提高7.81%与8.16%。

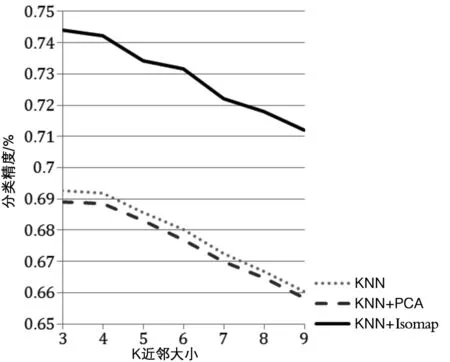
图4 随K近邻增加各分类方法的分类精度变化图

由以上实验结果可以看出,与原始K近邻算法以及先用PCA算法降维再进行K近邻算法分类的方式相比,本文提出的新算法能有效提高分类精度。并且尽管模型参数在变化,新算法能始终保持比较明显的分类精度优势。尤其是当训练样本数量降低时,新算法的分类精度有更为明显的提高。

4 结 语

本文尝试在Isomap非线性降维方法的基础上使用K近邻分类器进行高光谱遥感影像分类。在引入核函数方法后,本文有效地将两种算法相结合,不仅节约了计算成本,简化了算法实现步骤,并在最后通过实验证明这种算法的结合能有效提升原始K近邻模型的分类精度,其分类效果更高于简单使用PCA算法降维再分类的方式。近年来,越来越多类似Isomap的非线性降维方法被发明和改进,在今后的工作中我们希望尝试将更多类似算法核函数化并尝试用于传统分类器模型中,以提高其处理非线性观测数据的能力。

[1] 钟智,朱曼龙,张晨等.最近邻分类方法的研究[J].计算机科学与探索,2011(5):467～473.

[2] Houle M E,Kriegel H P,Kröger P and et al.Can Shared-Neighbor Distances Defeat the Curse of Dimensionality? [A].Statistical and Scientific Database Management-SSDBM,2010:482～500.

[3] Tenenbaum J B,de Silva V,Langford J C.A Global Geometric Framework for Nonlinear Dimensionality Reduction[J].Science,2000:2319～2323.

[4] Roweis S T,Saul L K.Nonlinear Dimensionality Reduction by Locally Linear Embedding[J].Science,2000,2323～2326.

[5] 杜培军,王小美,谭琨等.利用流形学习进行高光谱遥感影像的降维与特征提取[J].武汉大学学报·信息科学版,2011(2):48～52.

[6] 刘行波,武小军,周源.利用流形技术的遥感高光谱图像边缘检测[J].城市勘测,2010(S1):94～96.

[7] Xiong H.A Unified Framework for Kernelization:The Empirical Kernel Feature Space[A].Chinese Conference on Pattern Recognition-CCPR,2009.

[8] Balasubramanian M,Schwartz E L,Tenenbaum J B and et al.The Isomap Algorithm and Topological Stability[J].Science,2002,7a:7.

[9] Bengio Y,Paiement J,Vincent P and et al.Out-of-Sample Extensions for LLE,Isomap,MDS,Eigenmaps,and Spectral Clustering[A].Neural Information Processing Systems-NIPS,2003.

A Nonlinear K-Nearest Neighbor Classifier for Hyperspectral Remote Sensing Imagery Classification

Mo Wentong1,Zhou Yuan2
(1.Nanning Exploration&Survey Geoinformation Institute,Nanning 530022,China; 2.Tongji University College of Surveying and Geo-informatics,Shanghai 200092,China)

High dimensionality and nonlinearity are two main factors of Hyperspectral remote sensing data that will decrease the classification accuracy for most existing classification algorithms,such as K-nearest neighbor(KNN).This paper proposed a new nonlinear KNN classifier,which fuses the original KNN algorithm and Isomap algorithm by Kernel trick.This classifier does not need explicitly dimensionality reduction but still has the ability to analyze the nonlinearity by taking advantage of the Isomap algorithm.By cross-validation and parameter analysis in the experiments with hyperspectral test data,this new method has been proven to out-perform the original KNN and KNN with PCA algorithm in Classification Accuracy.

hyperspectral remote sensing;classification;KNN;nonlinearity

2014—04—13

莫文通(1981—),男,工程师,主要从事测绘工程管理、测绘信息化建设等技术工作。