基于角谱理论的频移插值法衍射计算
缪正祥,李重光,张中恒
(昆明理工大学理学院,昆明650500)
基于角谱理论的频移插值法衍射计算
缪正祥,李重光*,张中恒
(昆明理工大学理学院,昆明650500)
在衍射分布的离散计算中,当衍射距离增大时,满足抽样定理的抽样点数会随之增加,为了解决补零算法带来的计算量大、计算机内存溢出等问题,提出了一种频移插值法,在不改变抽样点数的情况下,获得更为丰富的频谱成分,计算每次插值后的光场分布,然后进行线性叠加,从而得到完整的衍射分布。结果表明,该算法可以避开衍射距离增大必须增加抽样点数这一离散计算限制条件,和传统补零算法相比,计算量极大地减小,并降低了对计算机内存的要求。
衍射;光栅;角谱;频移;插值
引 言
衍射问题是光学中遇到的最困难的问题之一,在衍射理论中很少存在某种意义上可以认为是严格的解[1-2]。根据角谱理论,光在自由空间中由衍射屏到观察屏的传播过程,在频域中等效为一个理想低通滤波器[3],在有限的观察面上,只能接收部分频率的衍射光波,离散计算时,需要选择合适的离散点数对空间频率离散化,当衍射距离增大时,为获得更为丰富的频谱成分,必须增加抽样点数以减小抽样频率间隔,但这样计算量会成倍增加[4]。
本文中提出一种频移插值方法,对物光波的频谱进行多次频移计算,在不显著增加计算量的前提下获取更小频率间隔下的频谱。频移过程是一个对物光波频谱插值的过程,经频移插值后,即缩小了抽样频率间隔又不需要增加抽样点数,确保衍射计算中不丢失太多的频谱成分,实现衍射分布的正确计算。
1 空间频率分析
以平面波为例,讨论1维坐标下,观察面上各点的空间频率随空间位置的变化关系。如图1所示,衍射面和观察面相互平行,衍射面中心和观察面中心在同一直线上,S为衍射面宽度,D为有效观察面宽度,观察面到衍射面的距离为z0,θ为平面光波与x轴的夹角。

Fig.1 Schematic of wave propagation
观察平面上的光场分布可以看作许多不同方向传播的单色平面波的线性叠加,每一平面波的振幅和相位都取决于相应的角谱[5-6],因此,观察面上任意点沿x方向的空间频率可表示为:
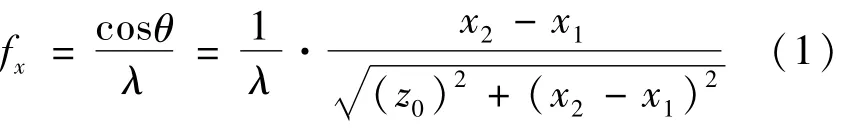
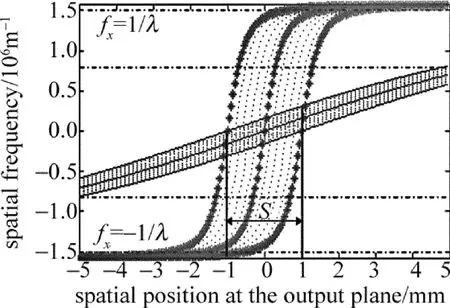
Fig.2 Spatial frequency changing with spatial position
图2 中,波长λ=632.8nm,衍射面宽度S=2mm,观察面尺寸D=10mm,“*”部分为z=0.5mm时的空间频率随空间位置的变化曲线,“-”部分为z=20mm时的空间频率随空间位置的变化曲线。衍射距离较小时,在观察面尺寸范围内,能保留较多的高频分量。随着衍射距离的增大,高频分量急剧减少,要完整地描述衍射分布,必须减小抽样频率间隔,这就意味着抽样点数必须增加。通过频移插值法不仅可以减小抽样频率间隔,而且能在不增加抽样点数的情况下保留下更多频谱成分[7]。
2 频移插值算法
离散数值计算时,须对变量x和y离散化处理,取离散间隔分别为Δx,Δy。衍射面上沿x,y方向的抽样点数分别为M和N,光波在z=0处的复振幅分布u(r,t;0)=u(rΔx,tΔy;0),根据离散傅里叶变换的定义,物光波的傅里叶频谱为:

式中,Δfx,Δfy为x,y方向的抽样频率间隔;m,r=根据衍射的角谱计算公式,衍射的角谱传递函数G(z0)可表示为:
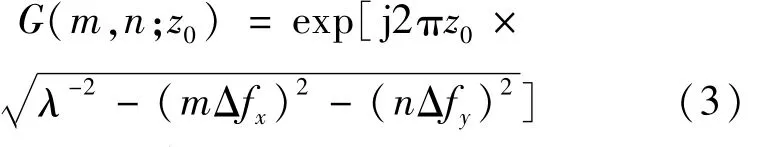
衍射光波的频谱为:

随着衍射距离的增大,在已定尺寸的观察面上,用同样离散条件所能描述别的高频分量减小,只有通过补零增加抽样点数才能更好的满足耐奎斯特抽样定理。补零后将M扩大P倍,变为P×M,N扩大Q倍,变为Q×N,大于M,N的部分用零补充[8]。则观察面的抽样点数为MP×NQ,其中MP=P×M,NQ=Q×N。
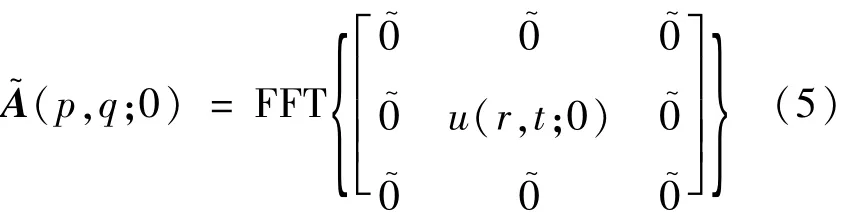
频移插值法通过将A(m,n;0)在频率域平移P×Q次后,再叠加得到A~(p,q;0),相当于对A(m,n;0)进行了P×Q次插值。频率间隔分别为Δfx=,设x和y方向的平移量分别为αΔfx和βΔfx(其中α=0,1,…,P-1;β=0,1,…,Q-1),则:

式中,∑表示将M×N大小的矩阵A线性叠加得到MP×NQ大小矩阵。根据傅里叶变换的性质,在频域的平移相当于在空域乘以一个线性相位因子[9]:

令:
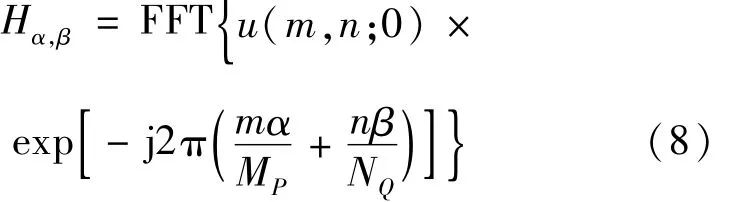
经传播距离z0后,衍射光波的频谱为:

观察面上的衍射光场分布为:
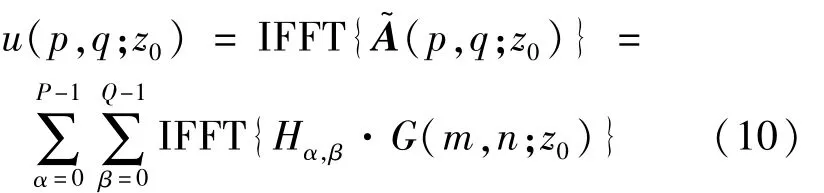
式中,IFFT为快速傅里叶逆变换(inverse fast Fourier transform,IFFT),Hα,β和G(m,n;z0)的大小为M×N,u(p,q;z0)的大小为MP×NQ,因此通过对M×N大小的矩阵作P×Q次快速傅里叶变换,叠加后可以得到观察面上的衍射光场[10-11],衍射图像的大小变为MP×NQ。而补零法是直接对MP×NQ的矩阵进行两次傅里叶变换得到衍射图像,因此(10)式较补零法计算量大大减小,能够在有限离散的观察面上得到更完整的衍射分布。


利用频移插值法计算时,有限离散点数的观察面上可以得到的衍射光波频谱宽度为:

频移插值法能够增加确定尺寸的观察面上衍射光波的频谱宽度,因此,能够更加精确地计算出衍射光波的光场分布。
3 数值模拟
为验证上述分析,编写计算程序,根据(10)式进行模拟计算。光波长λ=632.8nm,衍射物体为128pixel×128pixel的透光方孔,对应衍射面宽度S=2.5mm,抽样点数M=N=256,平移次数P=Q=2,观察面尺寸10mm×10mm。改变衍射距离z0的大小,得到不同距离上衍射光场的振幅及相位分布如图3所示。
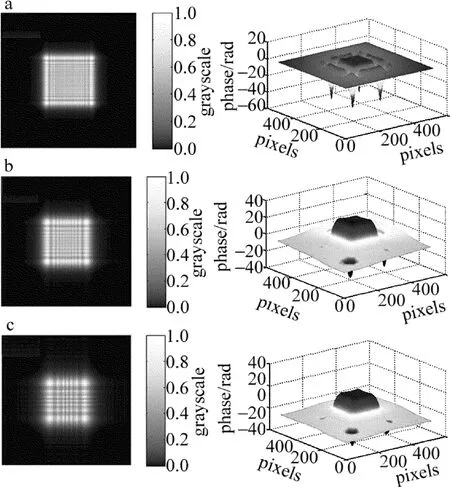
Fig.3 Amplitude and phase distribution in different propagating distance
图3 a、图3b和图3c中分别给出衍射距离为0.3m,0.6m和1m时衍射光场的振幅及相位分布,用于计算观察面上光场分布的MP×NQ总数达到512pixel×512pixel。通过频移插值法对256pixel× 256pixel大小的矩阵进行8次傅里叶变换得到衍射光场分布,而补零算法需要进行2次512pixel× 512pixel大小的傅里叶变换,由(12)式可知,频移插值算法能够在有限离散点数的观察面上得到更多频率成分的衍射光波。因此,频移插值法计算量较小,计算更为精确(根据数值模拟的条件编写计算程序,利用内存为4G的计算机进行实验计算,补零算法的计算时间约为0.058453s,频移插值法约为0.023571s,计算时间缩短近1.5倍)。
4 结 论
基于光传播的角谱理论,推导出远距离光波衍射的数值计算方法,该方法能够较好地满足耐奎斯特抽样定理。通过频移插值,能够在有限抽样的观察面上获得更多频率成分的衍射光波,可以更加准确地计算出衍射光场的空间分布情况。利用频移插值算法能够将大矩阵的傅里叶变换计算转化成多个小矩阵的傅里叶变换计算,大大减小了计算量、缩短了计算时间。
[1] WOLF B.Principles of optics[M].7th ed.Beijing:Publishing House of Electronics Industry,2005:342(in Chinese).
[2] GOODMAN JW.Introduction to fourier optics[M].3rd ed.Beijing:Publishing House of Electronics Industry,2011:46-61(in Chinese).
[3] LI JCh,XIONG B H.Information optics theory and calculation[M].Beijing:Science Press,2009:93-137(in Chinese).
[4] ZHANG BW,MA Y,ZHANG PP,et al.Simulation of Gaussian laser standing wave based on diffraction by straight edge[J].Laser Technology,2012,36(6):810-813(in Chinese).
[5] LIJCh.FFT computation of angular spectrum diffraction formula and its application in wavefront reconstruction of digital holography[J].Acta Optica Sinica,2009,29(5):1163-1167(in Chinese).
[6] MUFFOLETTO R P,TYLER JM,TOHLINE JE.Shifted Fresnel diffraction for computational holography[J].Optics Express,2007,15(9):5631-5640.
[7] KOZACKI T,FALAGGIS K,KUJAWINSKA M.Computation of diffracted fields for the case of high numerical aperture using the angular spectrum method[J].Applied Optics,2012,51(29):7080-7088.
[8] SU X Y,LIJT.Information optics[M].Beijing:Science Press,1999:34-47(in Chinese).
[9] LOBAZ P.Reference calculation of light propagation between parallel planes of different sizes and sampling rates[J].Optics Express,2010,19(1):32-39.
[10] LIU Y J.Diffraction field of orthogonal cosine-gratings[J].Laser Technology,2013,37(1):114-117(in Chinese).
[11] CHANG Sh,SANG Zh W,ZHUANG L.Calculation and analysis of spherical aberration on Gaussian image plane based on diffraction theory[J].Laser Technology,2012,36(3):405-407(in Chinese).
Diffraction computation with frequency shift interpolation based on theory of angular spectrum
MIAO Zhengxiang,LI Chongguang,ZHANG Zhongheng
(Faculty of Science,Kunming University of Science and Technology,Kunming 650500,China)
In the discrete numerical calculation of diffraction distribution,the total number of sampling points following sampling theorem increases with the augment of propagating distance.Although the traditional zero-padding method resolves this problem,the calculation load increases inevitably and PC’s memory can not afford.A novel frequency shift interpolation,i.e.,utilizing frequency spectrum calculation after shift in Fourier domain,was proposed.In the method,more sufficient spectrum components can be got without the increase of sampling number.A complete diffraction distribution is accomplished by splicing the light field obtained by spectrum of each shifted interpolation.The results show that the proposed method successfully evades the great sampling number caused by larger diffracting distance.Comparing with traditional zero-padding method,calculation load is decreased notably and the requirement to memory in numerical calculation is depressed.
diffraction;gratings;angular spectrum;shift in frequency domain;interpolation
O436.1
A
10.7510/jgjs.issn.1001-3806.2014.01.019
1001-3806(2014)01-0087-04
云南省应用基础研究基金资助项目(2008F04OM)
缪正祥(1986-),男,硕士研究生,主要从事信息处理方面的研究。
*通讯联系人。E-mail:2544248546@qq.com
2013-04-23;
2013-05-28

