艉轴密封装置Ω弹簧组的多参数优化设计
杨 敏, 柳建华, 吴堂荣
(1.上海理工大学能源与动力工程学院,上海200093;2.中国船舶重工业集团公司第七〇四研究所,上海200031)
艉轴密封装置Ω弹簧组的多参数优化设计
杨 敏1, 柳建华1, 吴堂荣2
(1.上海理工大学能源与动力工程学院,上海200093;2.中国船舶重工业集团公司第七〇四研究所,上海200031)
Ω弹簧组作为艉轴密封装置的重要组成部件,其结构补偿能力直接影响艉轴密封装置的密封效果.基于零阶算法,以单片弹簧的特征厚度、宽度、中圆半径和顶圆半径为设计变量,对Ω弹簧组进行多参数优化分析.通过有限元优化设计,分析求解Ω弹簧组各设计参数的响应以及径向刚度的最优解,优化后的刚度值比优化前的增加了11.5%.并对优化前后的Ω弹簧组分别进行谐响应分析,验证了Ω弹簧组径向刚度的优化设计对改变Ω弹簧组频率补偿能力的有效性,进而改善其结构补偿能力.
Ω弹簧组;结构补偿能力;零阶算法;多参数优化分析;谐响应
近年来,Ω弹簧组在一种新型艉轴密封装置中得到了广泛应用.利用Ω弹簧组受压时所产生的预紧力,使动摩擦副与静摩擦副之间产生一定的轴向压力,进而通过运动摩擦副起到端面密封效果.图1为艉轴密封装置结构示意图,该装置能够有效补偿轴系高速旋转时产生的轴向、径向振动,保证艉轴密封端面的平稳密封[1-3].Ω弹簧的结构补偿能力与弹簧组的径向刚度有直接的关系,径向刚度越大,其频率补偿能力越强,而对应的幅值补偿能力则会受到限制.
众多学者对改善Ω弹簧的结构补偿性能进行了试验研究.王晓军等[4]研究了Ω弹簧金属片的最大应力区、密封结构的刚度曲线、比压曲线以及振动补偿特性.胡举喜等[5]在此基础上对其进行优化设计,分别研究了3种金属弹簧片根部半径和弹簧片厚度对Ω弹簧组的寿命及补偿能力的影响,提出了根圆半径以及厚度对Ω弹簧刚度、补偿能力的影响.艉轴密封装置工作时,轴系高速转动所产生的轴向、径向振动作用于静环端面,再传递至Ω弹簧组结构.Ω弹簧组在安装时有一定的预压缩量,所以,对于艉轴密封装置,其频率补偿能力比幅值补偿能力更为重要.因此,本文基于零阶优化算法,以Ω弹簧组径向刚度为目标,对Ω弹簧组进行多参数优化设计,使其具有合适的结构补偿能力.
1 算法与模型
1.1 艉轴密封装置的基本结构
构成艉轴密封装置的基本元件有固定座、Ω弹簧组、夹紧环、静环、动环、驱动环和艉轴,如图1所示.通过Ω弹簧组的轴向补偿能力,为艉轴提供轴向密封作用.现主要研究Ω弹簧组对艉轴密封效果的影响.

图1 艉轴密封装置结构示意图Fig.1 Schematic diagram of ship seal device
1.2 零阶优化算法
Ω弹簧组优化设计时考虑的设计参数较为复杂,同时需要考虑最小安全因子对参数设计的限制,故考虑零阶优化算法,其计算流程如图2所示.零阶算法是在一定次数的抽样基础上,拟合设计变量、状态变量和目标函数的响应函数,从而寻求最优解.函数曲线(或曲面)的形式可采用线性拟合、平方拟合或平方加交叉项拟合[6-8].
采用平方拟合,则目标函数的拟合式为
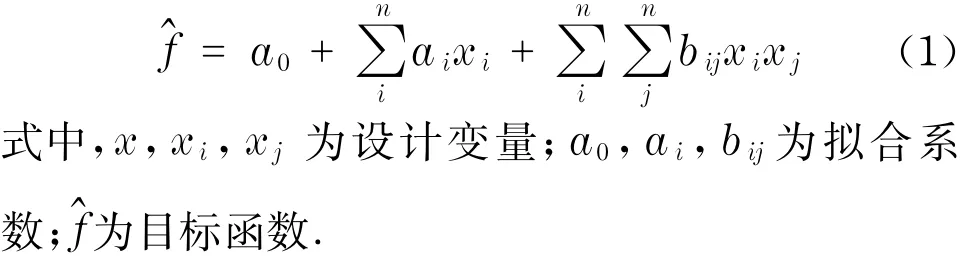
对于设计变量和状态变量的约束条件,可采用罚函数将其转化为无约束方程,如式(2)所示,从而将带有约束的优化问题转化成无约束的最小值求解问题.
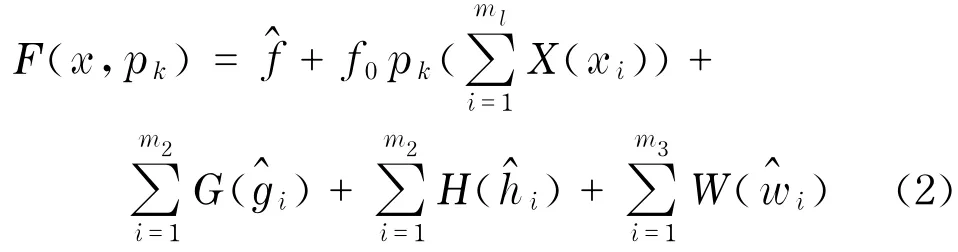
当设计变量(或状态变量)接近限值时,其罚函数值将急剧增加.

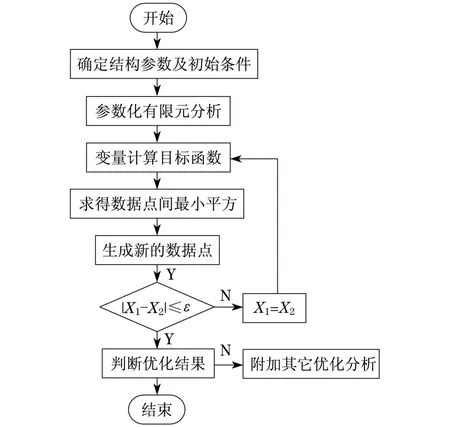
图2 Ω弹簧组优化流程图Fig.2 Process flow diagram of optimization forΩspring set
式中,xu,xl为设计变量的上下限;c1,c2,c3,c4为系数;ε是极小的正数.
转化为无约束问题后,即可采用序惯无约束极小化方法来搜索无约束目标函数.
1.3 有限元模型的建立
采用ANSYS Design Modeler对Ω弹簧组进行参数化建模.常规的单片Ω弹簧采用层合壳单元离散,可以简化有限元模型[9],但本文研究的Ω弹簧组由单片支撑弹簧、单片桥接弹簧和单片支架弹簧叠加组成,涉及到铺层方向上不同单片弹簧层间应力问题,层合板理论和相应的层合板壳单元不再适用.所以,使用3D结构单元Solid185模型对其进行有限元离散,更加准确地反映铺层之间的应力作用.单元Solid185含有8个节点,每个节点考虑3个自由度,则节点位移

式中,xN,yN,zN分别为节点N沿x,y,z方向的线位移.
1.4 数学模型
艉轴密封装置工作时受到轴向、径向振动作用及不稳定水压影响,会对艉轴密封装置的弹簧组结构产生位移载荷,Ω弹簧组的控制方程为

位移边界条件为
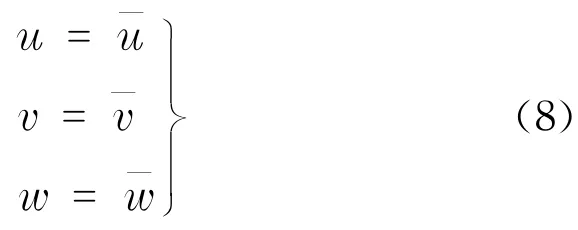
式中,σij,j为应力σij对j方向求偏导数;b表示作用在Ω弹簧组上沿着i方向的单位体积力;ui,j为ui对j方向的偏导数,εij为ioj面内的剪应变;Dijkl为弹性矩阵,可根据Voigt移动规则得出对应关系;为边界位移;εi,j为应变;σkl为应力;σij为ioj面上的应力;ui为位移分量;u,v,w为临近表面的位移.
2 多变量优化设计
优化设计是将实际问题首先转化为最优问题,然后运用最优化原理和方法,从满足各种设计要求及限制条件的全部可行方案中,选出最优设计参数,获得最优值.通过最优设计,能够使零件的力学性能得到改善,并且获得理想的结构布局和尺寸.
2.1 设计变量及约束条件
Ω弹簧组优化涉及到的设计变量分别为单片弹簧的特征厚度T,宽度W,中圆半径Rm以及顶圆半径Rt,如图3所示.
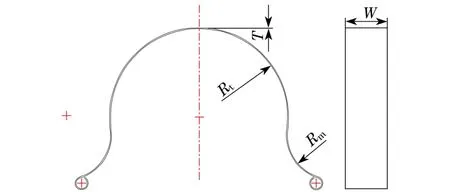
图3 单片Ω弹簧示意图Fig.3 Schematic diagram of singleΩspring
Ω弹簧组一般用于舰船艉轴密封等场合,其主要失效方式为屈服失效,故采用最大应力理论和畸变能密度理论进行强度校核.

式中,σmax为最大应力;[σ]为许用应力.
由于水下固有环境不同以及冲击波等突发频谱的不同,可以根据实际的情况,选择合适的安全因子.本设计中应该保证最小安全因子ξmin不小于1.45,即

2.2 目标函数
在矩阵位移法中,单元分析的任务是建立单元刚度方程,形成单元刚度矩阵,单元刚度方程为

待优化的Ω弹簧组要求得到最大的径向刚度,故优化目标函数确立为

式中,Ke为刚度矩阵;qe,Pe分别为位移向量、力向量;Kr为优化目标函数;Ke,r为径向刚度矩阵.
最终优化数学模型为

式中,T0,W0,Rm,0,Rt,0分别为Ω弹簧组单片初始特征厚度、宽度、中圆半径和顶圆半径;uT,lT,uW,lW,uRm,lRm,uRt,lRt分别代表对应参数的上限、下限系数;ξ0为设计安全因子.
3 优化分析
采用零阶方法对优化模型进行参数优化.Ω弹簧组的主体材料是蒙乃尔合金K500,弹性模量为1.78×1011,泊松比为0.32,屈服极限为1 345 MPa,安装时有20 mm的预压缩量,各状态变量的设计上、下限系数分别为(1±10%).
3.1 优化结果
选取最小安全因子为状态参数,径向刚度最小为目标函数,目标驱动优化结果,得到优化结果如图4所示,径向刚度与最小安全因子随着设计参数的改变而发生改变.

图4 优化结果权衡图Fig.4 Balanced figure for optimization results
表1分别列出了优化前后各个参数的取值,可以看出,在保证最小安全因子符合设计要求的情况下,特征厚度和宽度适当增大可以提高Ω弹簧组径向刚度;同时,中圆半径增大与顶圆半径减小对提高Ω弹簧组径向刚度起到增益作用.径向刚度由优化前的1 355 N/m增大为1 511 N/m,提高了11.5%,优化效果明显.

表1 优化前后参数对照Tab.1 Comparison of parameters before and after optimization
3.2 优化前后谐响应分析
为评价多参数优化对Ω弹簧组结构补偿能力的影响,在模态分析的基础上,对优化前后的Ω弹簧组分别进行谐响应分析.谐响应分析主要用于确定线性结构在承受随时间按正弦(简谐)规律变化的载荷时的稳态响应,分析过程中只计算结构的稳态受迫振动[10-11].
分析结果如图5所示,Ω弹簧组优化前在不同频率的最大响应幅值为22 mm,优化后可补偿最大响应幅值减小为13 mm,但同时其频率响应范围变大,即频率补偿能力增强,进一步验证了提高Ω弹簧组的径向刚度可以改善其结构补偿能力.

图5 优化前后谐响应图Fig.5 Harmonic response figure
4 结 论
a.基于零阶算法,以径向刚度为优化设计目标,建立Ω弹簧组多参数优化设计模型,实现了结构补偿能力的优化.
b.Ω弹簧组的特征厚度、宽度、中圆半径增加,顶圆半径减小,可以提高Ω弹簧组的径向刚度.
c.通过优化前后Ω弹簧组的谐响应分析,验证了优化设计的有效性.结果表明,提高Ω弹簧组的径向刚度能有效地提高Ω弹簧组的频率补偿能力,进而改善其结构补偿能力.
[1] 周斌兴,刘步丰,胡年丰.新型船舶艉轴端面密封装置的结构与设计[J].船舶工程,2009,31(2):24-26.
[2] 周斌兴,张能武.船舶艉轴密封Ω型弹性元件的设计与应用[J].船海工程,2006(6):60-62.
[3] 王瑾,王亚斯,段文珊,等.船舶艉轴密封装置动态环境下的热态性能模拟分析[J].上海理工大学学报,2013,5(4):361-364.
[4] 王晓军,胡举喜,杨海峰,等.新型艉轴密封装置的有限元分析与设计[J].舰船电子工程,2010,30(6):166-169.
[5] 胡举喜,常龙,杨海峰,等.船舶密封装置Ω弹簧组的优化设计[J].船舶工程,2010,32(2):82-84.
[6] 郭彤,李爱群,费庆国,等.零阶与一阶优化算法在悬索桥模型修正中的应用对比分析[J].振动与冲击,2007,26(4):35-38.
[7] More J J,Wright S J.Optimization software guide [M].Philadelphia:Society for Industrial&Applied Mathematics,1993.
[8] Zheng Q,Zhuang D M.Integral global optimization algorithms,implementations and numerical tests[J]. Journal of Global Optimization,1995,7(4):421-454.
[9] 刘宝山,赵国忠,顾元宪.复合材料层合板结构振动声辐射优化[J].振动与冲击,2008,27(12):31-35.
[10] 周小林,赵高晖,王国钦,等.水润滑艉轴承负载能力的分析[J].上海理工大学学报,2004,26(4):378-380.
[11] 周旭辉,杨俊.推力轴承轴向刚度对船舶轴系振动响应的影响[J].船海工程,2012,41(4):110-112.
(编辑:石 瑛)
Multi-parameter Optimal Design ofΩSpring Set for the Ship Seal Device
YANGMin1, LIUJian-hua1, WUTang-rong2
(1.School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China;2.China Shipbuilding Industry Corporation 704 Institution,Shanghai 200031,China)
The structural compensation ability ofΩspring set,as an important component of ship seal device,directly affects the sealing effect of ship seal device.Based on zero-order optimization method,multi-parameter optimization of theΩspring set was conducted with the design variables of the characteristic thickness,width,and the radiuses of both the middle and top circles.The responses of various design parameters and the optimal solution of maximum radial stiffness were analyzed.In conclusion,the radial stiffness increases by 11.5%after the optimization.Moreover,making the harmonic response analysis ofΩspring set before and after the optimization respectively,the results verify the effectiveness ofΩspring stiffness optimization to modify its frequency compensation ability,and thus improve its structural compensation ability.
Ωspring set;structural compensation ability;zero-order algorithm;multiparameter optimization analysis;harmonic response
U 664.21文献标示码:A
1007-6735(2014)05-0469-04
10.13255/j.cnki.jusst.2014.05.011
2014-01-05
杨 敏(1991-),男,硕士研究生.研究方向:机械密封技术的研究和模拟.E-mail:yangminshlgdx@163.com
柳建华(1956-),男,教授.研究方向:制冷系统节能技术与优化.E-mail:lwnlwn_liu@163.com

