基于模糊识别理论的无资料地区设计径流典型年选择

宋亚娅张 振黄振平葛 慧

(1.河海大学水文水资源学院,江苏南京 210098;2.陕西省地质调查中心,陕西西安 710016; 3.武警水电第二支队,贵州贵阳 550014)

基于模糊识别理论的无资料地区设计径流典型年选择

宋亚娅1,2,张 振3,黄振平1,葛 慧1

(1.河海大学水文水资源学院,江苏南京 210098;2.陕西省地质调查中心,陕西西安 710016; 3.武警水电第二支队,贵州贵阳 550014)

根据模糊识别理论,对参证流域设计径流典型年进行模糊识别,构建设计径流典型年的模糊识别模型;运用级别变量特征值对设计径流典型年进行优选。对设计径流典型年按照水文比拟法进行修正,移植到设计流域上,推求设计流域的设计径流典型年。研究表明:将模糊识别理论与水文比拟法相结合进行无资料地区径流的分析计算,为无资料地区设计径流典型年的选择提供了定量的计算方法,弥补了无资料地区传统定性的选择设计径流典型年主观随意性较大的不足。

无资料地区;设计径流典型年;模糊模式识别;模糊优选;水文比拟法

在中小型水利水电工程规划设计时,常因小流域缺乏实测径流资料或实测径流资料太短而无法展延,设计年径流量及其年内分配只有通过间接的途径来推求,水文比拟法是常用的方法之一[1]。由于无资料地区水文设计中不确定性的复杂性与普遍性特点,及设计径流典型年的典型与不典型问题属于模糊概念[2-3],因此无资料地区设计径流典型年的选择是一个具有不确定性的模糊模式识别问题[4]。鉴此,为客观地确定无资料地区设计径流典型年,减少不确定性因素对无资料地区水文设计的影响,本文在参证流域上构建设计径流典型年的模糊识别模型,优选参证流域上的设计径流典型年,并将其修正后移植到设计流域,进而推求无资料地区设计年径流量及其年内分配。

1 参证流域设计径流典型年的模糊识别

1.1 设计径流典型年指标的选择及指标规格化

设参证流域上选择设计径流典型年需要考虑m个指标(m个控制时段),样本容量为n。考虑水文系统中时段径流通常用皮尔逊Ⅲ型频率曲线加以描述,样本j控制时段i用模比系数Kij表示。为了进行模糊集分析,对Kij进行规格化处理。规定当Kij≤Ki1(控制时段i径流频率P=1%的模比系数)时,其规格化数rij等于1;当Kij≥Kic(控制时段i径流频率P=99%的模比系数)时,其rij等于0;在其之间者,其rij线性内插确定[4]。则样本j的m个控制时段模比系数的规格化矩阵为

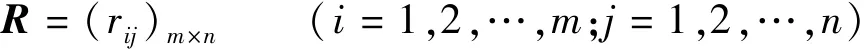
根据水利计算的要求,为每个控制时段选定c个频率标准值,即将n个样本依据其m个指标按c类标准模式加以识别,记设计径流典型年的标准模式为S:

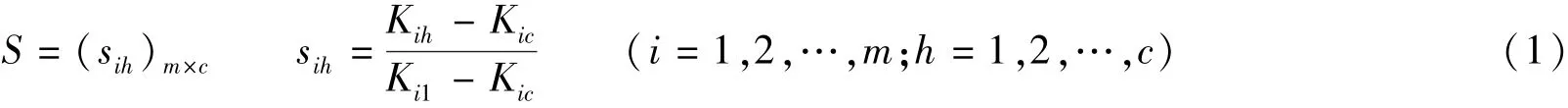
式中:sih——控制时段i级别h的模比系数Kih的规格化数。

1.2 指标权重的确定

采用可能度法[5-8]确定指标权重。根据语气算子级差与相对隶属度值,利用区间数运算法则对各方案的属性值进行集结。根据区间数的可能度公式,构造可能度矩阵,由最小方差法[4]求得权重为

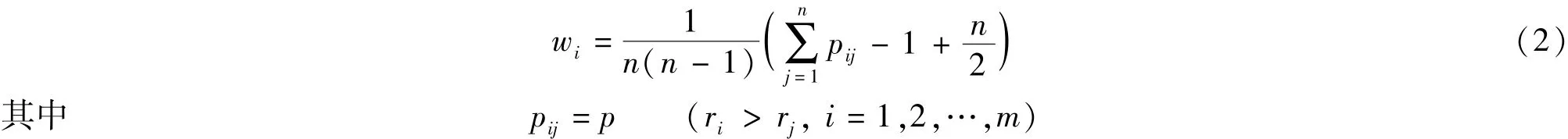
式中:ri、rj——语气算子的相对隶属度。

1.3 参证流域设计径流典型年模糊识别模型的构建

将n个样本依据其m个指标按c类标准模式加以识别,设j对h的相对隶属度为uhj,即各级别的相对隶属度矩阵

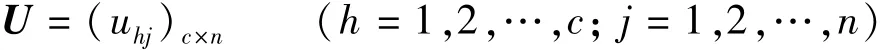
构造模糊模式识别模型[4]:

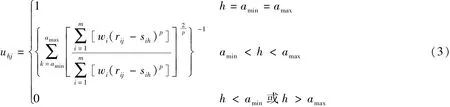
1.4 模糊模式优选

针对最大隶属度的原则[9-11]评判存在丢失信息过多使评判失真的缺陷,将级别变量特征值与相对隶属度相结合进行评判。式(4)为级别变量特征值Hj[12]的表达式与相应的级别判断:

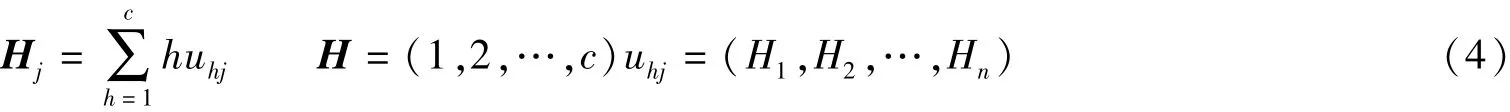
按照各级别的U和Hj,优选出符合设计频率要求的径流丰、平、枯不同类型的典型年。

2 设计流域设计径流典型年的计算

将参证流域上优选出的设计径流典型年按照水文比拟法移植到设计流域上,具体移植时考虑以下几种情况:(a)参证流域与设计流域的年降雨量基本相等、地理情况十分接近且两个流域的面积相差不大,可直接将参证流域的设计径流典型年移植到设计流域上;(b)参证流域和设计流域面积相差较大,或气候条件与下垫面条件有一定差异,参证流域优选出的设计径流典型年要进行面积修正;(c)设计流域与参证流域的自然地理情况相近,但降雨量差别较大,参证流域优选出的设计径流典型年要进行雨量修正。

3 应用实例

3.1 参证站设计径流典型年的模糊识别

陂下水库位于长汀县四都镇境内的陂下河上,坝址处无实测流量资料,根据参证流域选择的原则,选择观音桥水文站作为参证站。观音桥17 a(1958—1975年)的实测流量资料可作为比拟依据。经过统计分析坡下水库大多数的年份供水期为6个月,所以选择观音桥站连续最枯6个月为主要控制时段,连续最枯3个月和全年两个统计时段。各时段径流均以模比系数表示,选择观音桥站P=20%的丰水年典型,P=50%的平水年典型,P=80%的枯水年典型。

为每个控制时段选定11个频率标准值,即表示丰水的设计时段P的标准值为1%、3%、5%、10%、20%;表示中水年的设计时段P=50%;表示枯水的设计时段P的标准值为80%、90%、95%、97%、99%,各时段频率的径流模比系数如表1所示。

表1 各种时段、频率的径流模比系数Table1 Modulus ratios of runoff in different periods with different frequencies

3.2 指标权重的确定及指标规格化

采用可能度法计算指标权重,指标最枯3个月径流的权重w1=0.500,指标最枯6个月径流的权重w2= 0.333,指标年径流(水利年)的权重w3=0.167。

将观音桥站各时段径流样本的模比系数值规格化处理,得到样本集的时段径流模比系数规格化矩阵:

将各种时段频率的径流模比系数值规格化处理,得到时段径流频率的标准模式矩阵:

3.3 观音桥站设计径流典型年的模糊识别

按照式(3)可得各级别的相对隶属度矩阵:

3.4 观音桥站设计径流典型年的模糊优选

根据式(4)可得级别变量特征值:

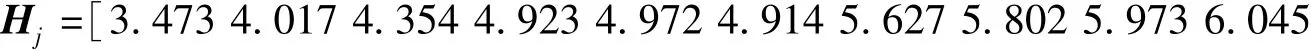
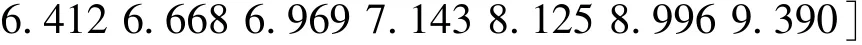
根据级别变量特征值,选择最近P=20%(h=5)H5=4.972的样本1962—1963年为丰水年典型;选择最近P=50%(h=6)H9=5.973的样本1966—1967年为丰平年典型;选择最近P=80%(h=7)H13=6.969的样本1970—1971年为丰平年典型。

由优选结果可知,1962—1963年3个时段径流的模比系数分别为1.478、1.339、1.216,在17个样本中与P=20%的相应时段径流模比系数最为贴近。1966—1967年3个时段径流模比系数分别为1.031、0.992、1.006,都与1.000很接近,这是典型中水年应具有的特点。1970—1971年3个时段径流模比系数分别为0.513、0.809、0.859,在17个样本中与P=80%的相应时段径流模比系数最为贴近。

4 坡下水库坝址处设计径流典型年的计算

按照水文比拟法,将观音桥站的设计径流典型年移植到坡下水库坝址处,考虑雨量与面积修正,表2为坡下水库坝址处的设计径流典型年。

表2 坡下水库坝址处的设计径流典型年Table2 Representative year of design runoff in Poxia Reservoir

5 结 语

a.鉴于无资料地区设计径流典型年中客观存在的模糊不确定性,运用模糊识别理论与水文比拟法,选择实际发生的与设计年径流量指标值最为接近的实际年径流作为设计径流典型年,为无资料地区设计径流典型年提供了比较全面的定量信息与依据。实例应用确定了无资料地区坡下水库P=80%设计枯水年典型、P=50%设计平水年典型与P=20%的设计丰水年典型。

b.基于模糊识别理论及水文比拟法进行无资料地区设计径流典型年的分析计算时,参证流域的选择将直接影响计算结果的好坏。无资料地区具体设计计算时,建议选择多个参证流域,优选得到多个设计径流典型年,根据无资料地区监测的确定性信息进行分析比较,以确定无资料地区设计径流典型年。

[1]叶守泽,詹道江.工程水文学[M].北京:中国水利水电出版社,2007.

[2]ZADEH L A.Fuzzy sets[J].Information and Control,1965,8:338-353.

[3]王本德,于义彬,刘金禄.水库洪水调度系统的模糊循环迭代模型及应用[J].水科学进展,2005,15(2):233-236.(WANG Bende,YU Yibin,LIU Jinlu.Fuzzy iteration model for reservoir flood operation[J].Advances in Water Science,2005,15(2): 233-236.(in Chinese))

[4]陈守煜.工程模糊集理论与应用[M].北京:国防工业出版社,1998.

[5]王淑英.水文系统模糊不确定性分析方法的研究与应用[D].大连:大连理工大学,2004.

[6]汪莲,琚泽进.基于信息熵的导流方案模糊模式识别方法[J].湖南工程学院学报:自然科学版,2010,20(2):79-82.(WAN Lian,JU Zejin.Entropy-based fuzzy pattern recognition method of diversion programs[J].Journal of Hunan Institute of Engineering:Natural Science Edition,2010,20(2):79-82.(in Chinese))

[7]王坚强,张忠.基于直觉模糊数的信息不完全的多准则规划方法[J].控制与决策,2008,23(l0):1145-1152.(WANG Jianqiang,ZHANG Zhong.Programming method of multi-criteria decision-making based on intuitionistic fuzzy number with incomplete certain information[J].Control and Decision,2008,23(l0):1145-1152.(in Chinese))

[8]李德清,谷云东.一种基于可能度的区间数排序方法[J].系统工程学报,2008,23(2):223-246.(LI Deqing,GU Yundong.Method for ranking interval numbers based on possibility degree[J].Journal of Systems Engineering,2008,23(2):223-246.(in Chinese))

[9]XU Zeshui,CHEN Jian.Some models for deriving the priority weights from interval fuzzy preference relations[J].EuropeanJournal of Operational Research,2008,184(1):266-280.

[10]陈守煜.基于可变模糊集的辩证法三大规律数学定理及其应用[J].大连理工大学学报,2010,50(5):839-844.(CHEN Shouyu.Three mathematical theorems of dialectics based on variable fuzzy sets and their application[J].Journal of Dalian University of Technology,2010,50(5):839-844.(in Chinese))

[11]葛慧,黄振平,王银堂,等.基于模糊识别理论的典型洪水的选择[J].水电能源科学,2011(3):54-56.(GE Hui,HUANG Zhenping,WANG Yintang,et al.Typical flood selection based on theory of fuzzy recognition[J].Water Resources and Power, 2011(3):54-56.(in Chinese))

[12]陈守煜,李敏,王淑英.可变模糊聚类迭代模型合理性分析与应用检验[J].大连理工大学学报,2009,49(6):933-936.(CHEN Shouyu,LI Min,WANG Shuying.Rationality analysis and application test of variable fuzzy clustering iterative model [J].Journal of Dalian University of Technology,2009,49(6):933-936.(in Chinese))

Selection of representative year of design runoff for ungauged basins based on fuzzy recognition theory

SONG Yaya1,2,ZHANG Zhen3,HUANG Zhenping1,GE Hui1
(1.College of Hydrology and Water Resources,Hohai University,Nanjing 210098,China; 2.Shaanxi Center of Geological Servey,Xi'an 710016,China; 3.The Second Branch of Water and Electricity Team of the Chinese People's Armed Police Troops, Guiyang 550014,China)

According to the fuzzy recognition theory,the representative year of design runoff in a reference basin was recognized,and a fuzzy recognition model of the representative year of design runoff was established.The eigenvalue of the grade variable was used to select the optimal fuzzy scheme for the representative year of design runoff.The results refined by the hydrologic analog method were applied to a design basin to determine the representative year of design runoff.This study shows that using the fuzzy recognition theory combined with the hydrologic analog method for runoff calculation in ungauged basins provides a quantitative calculation method for the representative year of design runoff,and makes up for the shortcomings of the traditional qualitative method,which is subjective and random.

ungauged basin;representative year of design runoff;fuzzy pattern recognition;fuzzy optimization; hydrologic analog method

TV123;P233

:A

:1000-1980(2014)01-0019-05

10.3876/j.issn.1000-1980.2014.01.004

2013-01 08

宋亚娅(1986—),女,河南商丘人,硕士研究生,主要从事工程水文与随机水文研究。E-mail:syy409@163.com