地震学百科知识（十二）——地震波散射＊

吴如山 谢小碧

1）美国加州大学圣克鲁斯分校，地球与行星科学学院，美国加州CA 95064

2）美国加州大学圣克鲁斯分校，地球物理与行星物理研究所，美国加州CA 95064

地震科普

地震学百科知识（十二）
——地震波散射＊

吴如山1）谢小碧2）

1）美国加州大学圣克鲁斯分校，地球与行星科学学院，美国加州CA 95064

2）美国加州大学圣克鲁斯分校，地球物理与行星物理研究所，美国加州CA 95064

广义地说，由地球介质的任何三维非均匀性引起的地震波场畸变均可称为地震波散射。不过，通常地震波散射是指由地球小尺度（与波长相比）非均匀性引起的、不适合用射线理论（几何射线）研究的地震波场畸变现象。例如，波场传播方向的偏折和分裂，P波和S波的相互转换，地震尾波的产生，地震波的走时和振幅横跨观测台阵的随机起伏变化等。

1 地球介质的不均匀性及地震波散射

随着对地球结构认识的深入，经典的球对称地球模型或分层地球模型常常不能满足研究的需要。人们逐渐认识到地球各个部分，包括地壳、地幔和地核都是横向不均匀的。其不均匀性的变化范围可以小到晶粒尺度，也可以大到整个大陆的尺度。

地球内部结构的非均匀性的存在往往揭示出地质构造活动的存在，例如，地震断层活动、板块俯冲、大陆碰撞、地幔对流或热柱活动等。目前，地震波是研究这些非均匀性的最有效的工具之一。

不同尺度的非均匀体对地震波传播具有不同的影响。全球性的非均匀性会使大地震激发出来的地球自由振荡的振型产生分裂。区域性的或局部的非均匀性会使地震波的走时、波形以及振幅发生起伏变化。核幔边界处的非均匀性会在地核影区产生散射波震相。小尺度的局部非均匀性会产生地震尾波并引起地震波的视衰减（散射衰减）。非常小尺度的非均匀体，例如介质中的裂隙或沉积地层中的薄互层，可以引起介质中的宏观各向异性。

对于具有平均尺度a和速度扰动强度指数˜v的非均匀体，它对地震波的影响可以用三个无量纲的特征量划分为不同的区域来讨论。这三个特征量是ka＝2πa／λ，L／a和˜v，其中k是波数，λ是介质中的波长，L是波传播的距离或非均匀区的尺度，˜v＝（δv／v0）rms是速度相对扰动的均方根值，v0是区域速度的平均值。以下是介质不均匀性对地震波传播的不同影响区域［1，2］（图1）。

（1）准均匀区。当ka＜0.01时，地震波很难探测到非均匀性的存在。利用等效参数，介质可以被近似看成均匀介质。

（2）瑞利散射。当ka≪1（例如ka＜0.1）时，散射能量正比于k4（振幅正比于k2）。在这一范围中的散射会引起明显的地震波衰减。

图1 地球中地震波散射现象的分类及不同近似方法的使用范围。a为非均匀体尺度；L为波传播距离；k＝2π／λ为波数；IS是散射波功率，I0是入射波功率

（3）大角度散射。当ka≈（例如0.1＜ka＜10）时，非均匀体的大小与波长接近，散射现象变得非常重要。入射能量以较大的角度被散射到各个方向。在这一范围中的散射现象也被称为共振散射或Mie散射。它对于形成地震尾波或引起散射衰减具有重要贡献。

（4）小角度散射或前向散射。当ka≫1时，绝大部分散射能量集中在波前进的方向。在这一范围，可以用抛物方程来近似全波波动方程。从物理上讲，这是因为大部分能量向前传播，所以可以用单向波方程来代替全波方程。在实践中，单向波方程的应用常常被推广到ka＞1。小角度散射问题与地震波的焦散现象、衍射现象和干涉现象有密切关系。它可以产生地震波走时和振幅的起伏，而由此产生的观测结果也可作为研究地球内部速度分布的数据。引入两个参数：

衍射参数：

散射强度参数：

其中衍射参数Λ是一个跟费涅尔半径与不均匀尺度之比有关的无量纲量；LF＝是沿传播路径L上的平均费涅尔半径；散射强度参数Φ可以被近似地理解为波通过距离L后所产生的均方根相位变化；aL是沿传播方向上非均匀体的尺度；ξ＝aL／a是非均匀性的各向异性比率。根据这两个参数，可以将小角度散射进一步细分为三个区域：

（1）几何光学区。这个区域处于ka＞1，Λ＜1以及ΛΦ＜2π。由于Λ＜1，沿着路径的平均费涅尔半径小于非均匀体的横向尺度，所以衍射现象可以被忽略。如果使用射线理论，同时还要满足ΛΦ＜2π。由方程（1）和（2），ΛΦ＝（L／a）3／2，所以使用射线理论受到传播长度和速度扰动强度v˜的限制。当ΛΦ＞2π，射线会分裂成互相干涉的微射线（microrays），问题会变得更加复杂。

（2）衍射区。这个区域由ka＞1，Λ＞1以及Φ＜2π来界定。由于Λ＞1，衍射现象必须加以考虑。Φ＜2π把问题限定在弱（非饱和）振幅起伏的范围。在衍射和几何光学的范围内，可利用里托夫（Rytov）近似（或平滑扰动近似）来处理问题。

（3）饱和区。这个区域由Φ＞2π和ΛΦ＜2π来界定。在这一区域中，振幅起伏趋于饱和，射线分裂为无数相互干涉的微射线。目前尚无有效的解析方法来研究这种现象。随机介质的散射理论可以用来导出一些关于波特性的统计学特征（更详细的分析，请参考文献［1-2］）。

2 地震波散射研究方法

2.1 确定性理论研究方法

在一个无源的线性弹性介质中，适合位移场u的运动方程为

其中ρ是密度，ui是位移分量，“，j”代表∂／∂xj，重复角标表示对于空间变量的求和，λ和μ是介质的拉梅常数。λ、μ和ρ均为位置χ的函数。为简便起见，这里仅考虑各向同性介质。

（1）适用于离散非均匀体的边界元方法。如果在非均匀体的内部和外部，介质分别是均匀的且二者之间有明确的分界面，则可以利用边界元或界面积分方程的方法求解和研究散射问题。

（2）利用扰动方法研究弱散射问题。当利用扰动方法来处理问题的时候，可以将非均匀介质分解为背景部分和扰动部分。例如，在方程（9）中，介质的参数可以被表示为

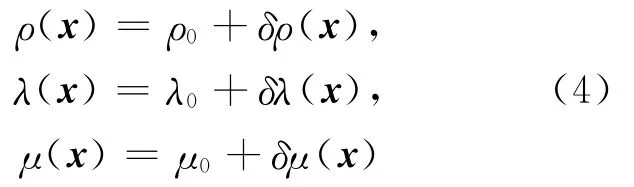
其中λ0、μ0和ρ0是背景介质参数，它们是均匀的或者是位置的缓变函数。δλ、δμ和δρ是介质参数偏离参考值的部分。与此类似，位移场也可以分解为

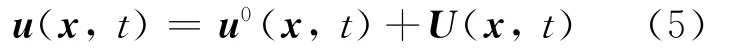
其中u0是对于背景介质的解，U是散射场。将方程（4）和（5）带入（3），得到

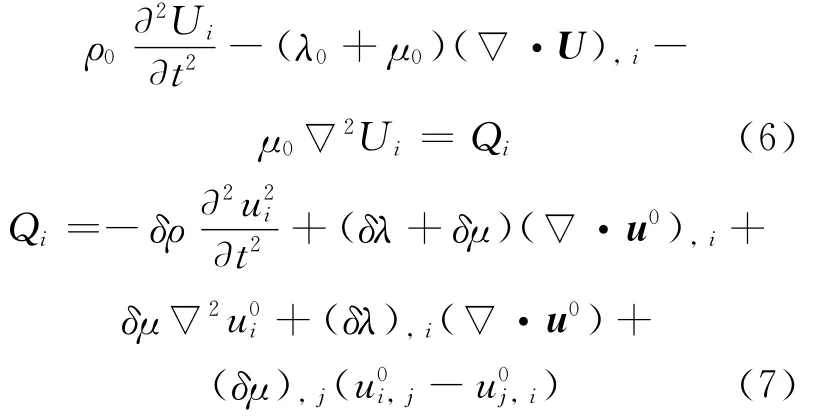
方程（13）是背景介质中的波动方程，Q（χ，t）是由于波场与非均匀性相互作用所产生的等效体力。引用格林函数G0ij（χ，t|χ′，t′）并利用表象定理，散射场可以表示为

如果散射场U相对于初始场u0来说比较弱，我们可以用初始场u0来近似式（8）中的总场u。这一近似被称为波恩（Born）近似。这时，式（8）变成对于散射场的显式方程，可以很方便地用来研究弱散射问题。

（3）高频近似方法：平滑介质近似。当非均匀体的尺度远远大于波长的时候（ka≫1），反向散射或大角度散射可以被忽略。如果波传播的距离不是很大，即费涅尔半径不大于非均匀体的尺度a，则传播方式在几何光学描述的范围内（见图1）。其中仅有聚焦现象起作用。通常，我们并不把几何光学描述的范围包括在散射的范畴之内。但是，当传播距离加大，以至于费涅尔半径大于非均匀体的尺度a时，问题就进入了衍射的范畴。此时，我们必须考虑衍射和干涉现象。在这种情况下里托夫近似是适当的方法，因为它同时适用于衍射范畴和几何光学范畴。

（4）高频近似方法：间断面散射问题。如果非均匀体的尺度远远大于波长，它与周围介质的性质有很大差别且由清晰的间断面分隔（例如边缘、劈形体、块体、空腔、裂缝等），可以利用很多高频近似的方法。例如，适用于衍射的几何理论。当非均匀体是由弯曲界面的层状结构组成，且与波长相比它的分界面比较光滑，则可以利用物理光学近似（也称为克希霍夫近似）的方法。

2.2 随机理论方法和介质的统计特性

对于非常复杂的介质，特别是当波散射牵涉到大量的不规则小尺度非均匀体时，确定性的研究方法或者非常困难，或者根本不可能。在这种情况下，我们通常采用随机介质散射的研究方法。例如，当波传播距离远大于不均匀尺度，即L／a≫1时（见图1），就非常适合于用随机方法来研究。对于随机介质，我们并不奢望能确定每个小非均匀体的位置、形状和参数，而只是希望能观测反演出它们的统计特性，用几个统计参数来表征它们：例如它们的平均尺度或功率谱（即非均匀性在不同波数下的能量密度），介质参数变化起伏的均方根值等。如果数据足够多，还可以求出这种统计参数随空间的变化。散射波场的统计特性有波场的相关函数或相干函数，包括空间相关，频率相关，角度相关，或它们的联合相关函数，用这些相关函数可建立波场统计特性与非均匀体统计特性之间的关系。一旦这两种统计特性之间的关系被建立（有了随机散射的正演模型），就可根据观测数据的统计特征来反推地下非均匀体的统计特性了。

随机散射理论大致可分为弱散射理论和强散射理论［3］。

（1）弱散射理论。在非均匀性很弱或传播距离较小的情况下，可根据确定性理论中的微扰法，先用波恩近似或里托夫（Rytov）近似（常与抛物近似相结合）得到散射场的公式，然后再用集平均（ensemble average）的方法求波长相关函数（或统计矩）。这样就可得到波长相关函数与介质统计参数的关系。

（2）强散射理论（多次散射理论）。在强散射时，多次散射变得明显而重要。波恩散射等单次散射理论已不再有效。在强散射情况下曾推导出2阶和4阶统计矩方程。但在地震波研究中应用较少。地震波，特别是尾波理论研究中应用较多的是辐射传输（radiation transfer）或称能量传输（energy transfer）理论。在这种理论中，波长的相位及干涉效应均被忽略，而只考虑在多次散射时的能量传输关系。因此这种方法本质上是一种高频近似。而辐射传输理论本身也是在处理粒子散射时发展起来的。在处理强散射下长距离波传播时，即当传播距离远大于波散射的平均自由路径（相当于单次散射的有效范围）时，详细的波相位信息可被忽略，而集中研究波传播的能量关系。在理论与观测对比时，只注意地震图包络的衰降，而不管波形变化的细节。

2.3 数值模拟或物理模型实验

最常用的数值模拟方法是有限差分法、有限元法、边界元法、谱元法（spectral elements）和晶格玻尔兹曼方法，还有一些建立在单向波基础上的计算方法，例如单向（one-way）及单返折（one-return）弹性波广义屏方法。数值模拟方法的最大优点是适用性强，原则上可以处理任何散射问题。不过考虑到实际效率，通常利用理论方法对散射问题进行一定的近似，然后进行数值计算。

物理模型实验是研究散射问题的另一种有用工具。模型通常由金属、树脂或玻璃钢材料制成。实验所用的频率通常为几十kHz至1MHz的超声波。使用的P波波长通常为5～100mm，S波波长为3～60mm。散射体通常利用在材料上打孔或在材料中掺入其他成分来产生。在应用地震学中，水槽或固体槽的模型实验也很普遍。

3 地震波散射的各种现象及其观测应用

3.1 地震尾波的观测和应用研究

地震波散射在地震图中产生的最显著的现象之一就是地震尾波的产生。地震尾波是指出现在主要地震震相（例如P波、S波或面波等）之后不规则的波列，它就像是这些震相的尾巴。在地震学的早期，这些尾波常被视为噪声干扰。地震学家安艺敬一（K.Aki）最早开始研究尾波及其应用，并认为尾波是由地球内部小尺度不均匀性对地震波散射而产生。现在大家都承认尾波带有大量的关于地球内部小尺度不均匀性的信息。提取并研究这些散射波携带的信息也成为地震学的一个分支，并日益得到重视。对于震中距为200～300km的地方震，在S波之后的尾波通常被称为S-尾波（S-coda）。在远震P波之后的尾波通常被称为P-尾波（P-coda）。对于地方震产生的S波尾波已经做过相当细致的研究［4］。

3.2 透射地震数据中振幅和相位的起伏

地震波通过介质时，介质中的非均匀性使地震波产生衍射和焦散现象。由此会产生波前的不同参数（例如，振幅、到时、入射角等）的起伏变化。地震波到时和振幅的起伏已经在NORSOR、LASA等大型地震台阵以及一些区域地震台阵中被广泛观测到了。对于来自不同震源的数据，即使入射方向只相差一个很小的角度，波前的起伏就会有很大的差别。另一方面，对于来自同一方向的地震波，台阵中相距很近的台站观测到的信号往往有比较大的差别。这些差别中含有关于地壳、上地幔和岩石层中非均匀性的宝贵信息。在台站和震源分布相对于所要研究的结构有足够的密度时，各种层析成像等确定性方法可被应用。但对高频地震波（高于1Hz），小尺度非均匀性分布广泛的情况下，随机散射的理论可以用来反演地下非均匀体的统计特性，例如非均匀体的平均尺度，均方根速度扰动，非均匀层厚度，或非均匀体的功率谱。这种小尺度非均匀体的统计参数可以给地球内部的动力过程提供有用的信息。

3.3 核幔边界处的地震波散射

由地幔底部和核幔边界处小尺度非均匀性产生的散射波在震中距为120°～142°之间以PKIKP和PKP前驱波的形式出现。这种波为研究地球深部的介质特性提供了非常宝贵的信息。散射波通常比较弱，且在近3000 km的传播过程中受到很大衰减，因此常常需要在地核造成的直达波影区中观测，或者利用台阵技术通过叠加等方法来提取有效信息。近十几年来，随着数字地震资料的增加，特别是地震台阵和高密度流动台网的应用，相干叠加的方法获得了很大发展。通过对PKP散射资料的研究，目前一般认为在核幔边界之上数百千米的D”层中存在百分之几的非均匀性，非均匀性的形式比较复杂。例如，散射波的存在表明其中有小尺度（10～30km）的散射体。而散射能量的空间分布揭示出存在尺度为1 000km以上的区域性变化。某些区域性特征与地球的大尺度过程存在一定的对应关系。这些观测结果为研究若干地球动力学问题，例如热柱起源、残余板块的下沉深度、下地幔介质物理性质与化学成分的不均匀性、以及地核与地幔的耦合等提供了约束条件。类似地，也可以利用对PKKP波的散射来研究地核中的不均匀性［5］。

3.4 裂隙产生的散射及由此产生的各向异性

当散射介质中存在大量微小的随机散射体的时候，如果单一散射体的尺度远小于波长，则个别散射体对于波传播的影响并不重要。人们更感兴趣的是大量散射体作为整体对波传播的影响。在这种情况下，利用随机方法研究散射问题更为合适。如果非均匀体在介质中的分布是大致均匀的，则可以将这种介质处理为具有某些等效介质参数（例如等效速度、等效衰减、等效频散和等效反射率等）的“准均匀”介质（见图2）。如果单一散射体（例如裂隙）是各向异性的，且众多散射体在介质中的排列具有某种优势取向，作为整体，介质可能表现出某种宏观各向异性。在世界上的许多地区已经观察到由这种宏观各向异性所造成的S波分裂等现象。

3.5 多次散射（multiple scattering）和干涉测量（interferometry）

在尾波研究中，由于众多的小尺度非均匀体以及杂乱和多次散射，使得尾波的相位信息很难被利用。因此，传统的尾波观测和理论只研究其包络和能量关系。但近年来由于干涉测量技术（例如在高空和卫星干涉测量仪中）的发展，使得在尾波相位信息的利用上也取得了很大发展。

在复杂的高频地震图中（在天然地震中一般指高于1Hz的地震图；勘探地震中信号频率可以从几分之一到几十或几百赫兹，都应属于高频地震），从概念上讲可以把波（或事件）分为初次波（primary wave）（包括一次穿透、反射波或一次散射波）及多次波（多次反射或散射波）。在传统的地震图分析及物性成像研究中，反演数据多集中在利用初次波上，往往把多次波当成噪声干扰。在利用了干涉测量（interferometry）后，这种多次波就成了有用的信息。如果把初次波以外的成分都视为尾波，则这种多次波干涉测量的方法也可称为尾波干涉测量法。这种技术主要是利用叠加求相关函数的方法，即测量不同时移（time-shift）或空移（空间位置变化）的相关系数，以求把相干事件的时差（或相位）测量得更精确。

（作者电子信箱，谢小碧：xxie＠ucsc.edu；许忠淮：xuzh＠cea-igp.ac.cn）

［1］［美］安艺敬一.地震波的散射与衰减（上）.李玉澈，卢寿德等译，吴建春，刘洪校.北京：地震出版社，1993

［2］Sato H，Fehler M，Wu R S.Scattering and attenuation of seismic waves in the Lithosphere.William H.Lee K，Kanamor H，Jennings P，Kisslinger C（Eds）.Intern.Handbook of Earthquake ＆Engineering Seismology，Part A.Academic Press，2002：195-208

［3］Sato H，Fehler M.Seismic Wave Propagation and Scattering in the Heterogeneous Earth.Springer-Verlag，New York，1998

［4］Snider R.The theory of coda wave interferometry.Pure and Appl.Geophys.，2006，163：455-473

［5］Wu R S，Maupin V.Advances in wave propagation in heterogeneous Earth∥Dmowska R（ed）.Advances in Geophysics，Vol.48，Academic Press，Elsevier，2006

P315；

E；

10.3969／j.issn.0235-4975.2014.06.007

2014-04-21。