基于序列特征筛选与支持向量回归预测蛋白质折叠速率

李 咏 周 玮 代志军 陈 渊 王志明 袁哲明

(湖南农业大学,湖南省作物种质创新与资源利用重点实验室,长沙410128;湖南农业大学,湖南省植物病虫害生物学及防控重点实验室,长沙410128)

1 引言

多肽正确折叠成蛋白质才能发挥生物活性,错误的折叠不仅使蛋白质失活,且可导致疯牛病、阿尔茨海默病等.1折叠速率预测对阐明蛋白质折叠机理意义重大,在酶工程、蛋白质工程等领域应用前景广泛.质谱、核磁共振等传统实验测定折叠速率的方法耗时费力,2机器学习从已有数据出发,通过建立蛋白质折叠速率与诸因子之间的回归模型,可实现折叠速率的快速预测并解析诸因子的影响大小,帮助认识折叠过程.

蛋白质按折叠类型分为二态、多态和混态三种,按结构类型分为全α、全β、混合型三种.目前已知折叠速率的蛋白质数量较少,按类型进一步细分后样本容量偏小,建模时易出现过拟合、预测精度虚高;且待测蛋白质折叠类型或结构类型未知时,应用受限.故本文选择统一建模,不按类细分样本.

折叠速率预测的第一个关键是回归模型选择.由于蛋白质折叠是一个复杂的过程,且目前已知折叠速率的蛋白质数量较少,故本文选择基于结构风险最小、非线性、适于小样本的支持向量回归(SVR)为基本建模工具.

折叠速率预测的第二个关键是蛋白质表征,包括三级结构、二级结构和一级结构表征描述符三类.三级结构表征的描述符如接触序CO、总接触序ACO和有效接触序ECO等,3-8由于多数蛋白质三级结构尚未测定,应用受限.二级结构描述符如二级结构含量SSC、有效长度Leff等,9,10多从一级结构间接预测而得,描述符本身具有预测误差,再次代入非线性SVR模型存在误差放大风险,预测精度偏低.一级结构(氨基酸序列)描述符如CI、RSA、pse-ACC等,11-15多基于序列组分特征或以残基某几种物理化学性质直接算得,计算简便,更具推广应用价值;但存在组分特征未充分考虑序列的上下文关联、残基性质选择多依赖经验(与折叠速率相关的残基性质不全、无关或冗余均会导致预测精度下降)、对不等长肽处理困难等弊端.

折叠速率预测的第三个关键是特征(描述符)筛选.特征筛选可去除无关与冗余描述符,但这种筛选过程同样应该是非线性的.本实验室16,17前期基于支持向量机(SVM)发展了高维特征选择新方法二元矩阵重排过滤器(BMSF)与低维特征选择新方法多轮末尾淘汰(WDEM).

综上,本文仅基于氨基酸序列,提取多种组分特征与关联特征,经改进BMSF与多轮末尾淘汰非线性筛选,建立了折叠速率与保留描述符的SVR回归模型,进一步以SVR非线性解释体系分析了各保留描述符对折叠速率的影响.

2 数据和方法

2.1 数据来源

115个蛋白质ID与对应的折叠速率值1,2,14,18见表1,氨基酸序列取自PDB数据库(http://www.rcsb.org/pdb),折叠速率值以实验值的自然对数lnkf表示,kf的单位为s-1.

2.2 序列表征

一条氨基酸序列可由其组分特征、上下文关联特征与长度来特异性地表征.

2.2.1 天然氨基酸单残基尺度组分特征

对长度为L的氨基酸序列,组分尺度为R,R个氨基酸残基组成的串α1α2…αR可交叠出现频次为f(α1α2…αR),其中αi,i=1,2,…R,代表20种天然氨基酸的一种,则α1α2…αR串在序列中出现概率为:

随尺度变大,特征维数增加迅猛(如R=3,特征有8000维);而序列长度有限,特征矩阵将相当稀疏,对建模预测不利.故本文此处基于20种天然氨基酸仅提取单残基尺度R=1的组分特征,其R=2时的二联体组分特征将在下文k-space特征中k=0时涵盖.每条序列可得20维特征.

2.2.2 重分类氨基酸多尺度组分特征

氨基酸重分类可降低特征维数,凸显残基某种性质的作用.20种天然氨基酸按支链官能团可分成8类(表2).取R=1-3,每条序列按式(1)可得8+64+512=584维多尺度组分特征.

2.2.3k-space特征

上述两种组分特征仅考虑了3个以内残基相邻的情形,而蛋白质拓扑结构与稳定性和残基的远距离接触有关,19且可由k-space一定程度表征.20种天然氨基酸相隔k个残基的成对残基在序列中出现概率(C)为:

表1 115个蛋白质样品信息列表1,2,14,18Table 1 Information of 115 protein samples1,2,14,18

式中,k为space间隔,i和j为20种天然氨基酸中的一种,L为序列长度.n位置残基为i,n+k位置残基为j时Si,j(n,n+k)=1,否则为0.k-space既包含尺度为2的组分特征,又包含一定程度的上下文关联特征.取k=0-10,每条序列可得400×11=4400维k-space特征.

表2 20种天然氨基酸分类Table 2 Classification of 20 natural amino acids

2.2.4 地统计学关联(GSA)特征

k-space仅考虑了成对残基间的上下文关联.本文收集了20种天然氨基酸的544种物理化学性质(命名为PBF544),其中531种性质来自AAindex数据库,2013种性质引自文献.15,21,22因不同性质值差异较大,每种性质按20种氨基酸的最大最小值规格化到0-1之间.

地统计学基于区域化变量理论,引入半变异函数研究空间分布的结构性和随机性,可用于表征蛋白质中全部残基某种物理化学性质间的关联且不受序列是否等长的限制.对长度为L的给定蛋白质序列,对应某一物理化学性质按PBF544可转换为数值系列z(xi),i=1,2,…L,其半变异函数值r(h)为:

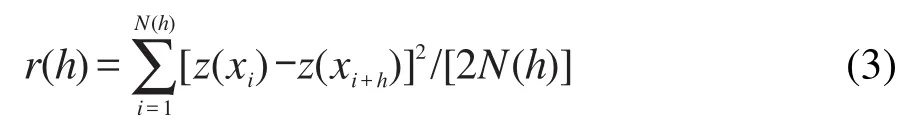
其中,h为间隔距离,N(h)为距离为h的数据对(xi,xi+h)的个数,z(xi)和z(xi+h)分别为点xi和点xi+h处残基的物理化学性质值.

若数据集最短序列长度为Lmin,规定max(h)=INT(Lmin/2).本文数据集最短序列长度为16,h取1-8.则每条序列可得544×8=4352维地统计学关联特征.

2.2.5 长度特征

前述组分特征等在计算概率时扣除了序列长度的影响,但多态折叠蛋白的折叠速率与序列长度负相关显著,19故本文以lnL表征序列长度特征.

综上,每条序列特征维数合计为20+584+4400+4352+1=9357.可以想象,其中必定存在大量与折叠速率无关或冗余的特征,需进行特征筛选.

2.3 特征筛选

2.3.1 高维特征粗筛

BMSF算法简述如下:设单因变量原始训练集形为(y,x),有n个样本,m个特征.每个特征有1(选取)和0(不选取)两种情形.产生一个元素为1或0的K×m随机矩阵,限定每列1与0的个数相同,本文取K=500.从随机矩阵的每行选取值为1的矩阵元素并找出原始训练集中对应特征,以SVR经10折交叉测试获得K个MSE值.K个MSE(因变量)与K×m随机矩阵(自变量)组成新训练集并训练建模,随机矩阵的某列元素0、1互换后(其它列不变)为测试集,预测得K个MSE0与K个MSE1,若则剔除相应特征;遍历m次,得第一轮保留特征.重复上述过程,经多轮筛选至没有特征可剔除为止.16,17

因BMSF中间矩阵是随机生成的,不同次执行所得最优特征子集可能不同,本文对此进行改进:重复执行BMSF 50次,得到50套最优子集.合并出现频次大于等于某个定值的特征产生频次子集,根据10折交叉测试结果,得到更为可信的高频特征子集.

2.3.2 多轮末尾淘汰精细筛选

WDEM算法简述如下:对数据矩阵(yi,xij),i=1,2,…,n,j=1,2,…,m′,SVR交叉测试得初始MSE0,第一轮依次去除第j个特征,SVR交叉测试得到对应的MSEj,若min(MSEj)≤MSE0,则剔除相应特征并进入下一轮筛选,反之筛选结束.23,24

2.4 模型评估与解释

基于保留描述符和全部样本可构建SVR模型.模型评估常用交叉验证、Jackknife检验或独立测试.由于已知折叠速率的蛋白质样本较少,同类研究常不划分独立测试集.为方便与文献1,11-15进行比较,本文同样采用Jackknife检验.评价指标为均方误差(RMSE)和相关系数R,RMSE越小、R越大,回归模型性能愈优:

式中,n为样本数,yi和^i分别为第i个样本的真值和预测值,为所有样本真值的均值.

SVR缺乏一个显性的表达式,可解释性差.本室前期基于F测验,对SVR建立了一套较完整的非线性解释性体系,包括模型回归显著性测验、单因子重要性显著性测验、单因子效应分析等,并验证了其合理性与有效性.23,24F统计量由下式给出:

其中,U为回归平方和:为剩余离差平方和:为保留特征数,F的自由度为表明在α水平上非线性回归显著.

本文BMSF高维特征粗筛、多轮末尾淘汰精筛、SVR建模和非线性解释体系等采用自编MATLAB程序通过调用LIBSVM3.1软件包25实现.多数情况下径向基核较其它核函数有更优的泛化推广能力,26本文试算后核函数选用径向基核.核函数参数采用Python默认范围、步长经格点搜索自动获取.

2.5 参比模型

文献参比模型包括多元线性回归(MLR)、基于SVR的前向-序贯后向特征选择方法(FFS-SBSSVR);基于本文描述符的参比模型包括SVR、遗传算法-偏最小二乘(GA-PLS)、27岭回归与SVR(RRSVR).28

3 结果与分析

基于115个样本和9357个初始特征,数据集10折交叉测试的RMSE=3.94,R=0.30.50次BMSF高维特征初筛后,得到50套子集,分别进行多轮末尾淘汰,平均保留特征个数、RMSE、R分别为31、1.59、0.91,可见特征筛选效果明显.合并出现频次大于等于某个定值的特征产生频次特征子集,频次子集进行10折交叉测试,结果见图1,可见出现7次及以上的特征10折交叉测试RMSE最小、R最大.故合并出现频次大于等于7次的特征得到高频最优特征子集.对高频最优特征子集进一步实施多轮末尾淘汰精筛,最终得到23个保留描述符.

基于23个保留描述符建立SVR23模型,其F=63.42>F0.01/23(23,91)=2.70,表明模型非线性回归极显著.SVR23模型Jackknife检验的实验值与预测值见表1和图2,其R=0.95,RMSE=1.34.可见,改进BMSF进一步提高了模型精度、减少了保留描述符个数.

图1 不同频次子集10折交叉测试的RMSE和RFig.1 RMSE and R values of 10-fold cross-validation of different frequency subsets

图2 Jackknife交叉检验的蛋白质折叠速率实验值与预测值Fig.2 Relationship between the experimental and predicted protein folding rates with Jackknife cross-validation

参比模型中,GA-PLS选取3个潜变量;RRSVR先经岭回归筛选得121个描述符,再经多轮末尾淘汰得到23个保留描述符.各模型Jackknife检验结果列于表3.可见,SVR23在所有参比模型中表现最优.

23个保留描述符包括1个长度特征、12个kspace特征、8个地统计学关联特征和2个氨基酸分八类时的三联体特征(表4),可见:(1)序列长度是影响蛋白质折叠速率的最重要因素.早期研究认为二态折叠蛋白折叠速率与序列长度的相关性较低,3但随后发现多态折叠蛋白折叠速率与序列长度显著负相关,19且序列长度的自然对数lnL优于其它形式(L,L1/2,L2/3).29(2)单个氨基酸组成(无论是分20类还是分8类)对折叠速率影响不大.(3)地统计学关联特征多涉及残基形成α-helix、β-turn等二级结构性质,且以中短程关联为主(h=1-6).(4)k-space反映的是成对残基间的关联,保留描述符中成对残基较为分散,以脂肪族氨基酸残基为主,且T、P、W、C残基参与的成对残基无一入选,关联距离k=1-10,k=0反映的相邻残基对(二联体)无一入选.脂肪族氨基酸含有疏水侧链,在蛋白质折叠过程中有序聚集,形成疏水内部结构,影响蛋白质折叠速率.1(5)氨基酸分八类时,疏水脂肪氨基酸+酰胺+疏水脂肪氨基酸、酸性氨基酸+酸性氨基酸+羟基氨基酸的两种三联体对折叠速率有重要影响.综上,蛋白质折叠速率与序列长度、三联体残基组分特征、中短程关联特征等相关密切.

保留描述符的单因子重要性、显著性测验结果表明,其F值均大于临界值F0.01/23(1,91)(13.33),保留描述符对蛋白质折叠速率的影响极显著(表4).其单因子效应分析结果见图3,可见23个保留描述符可明显分为三类:第一类为序列长度(No.1)和地统计学关联特征(No.2、No.4、No.5、No.7、No.13),其排序整体较为靠前,与折叠速率负相关;第二类是8个kspace 特 征 (No.3、No.12、No.15、No.16、No.18、No.20、No.22、No.23)和1个氨基酸分八类时的三联体特征(No.10),与折叠速率同样均为负相关;第三类特征与折叠速率正相关,包括1个氨基酸分八类时的三联体特征(No.6)、4个k-space特征(No.8、No.9、No.11、No.21)和 3 个地统计学关联特征(No.14、No.17、No.19).

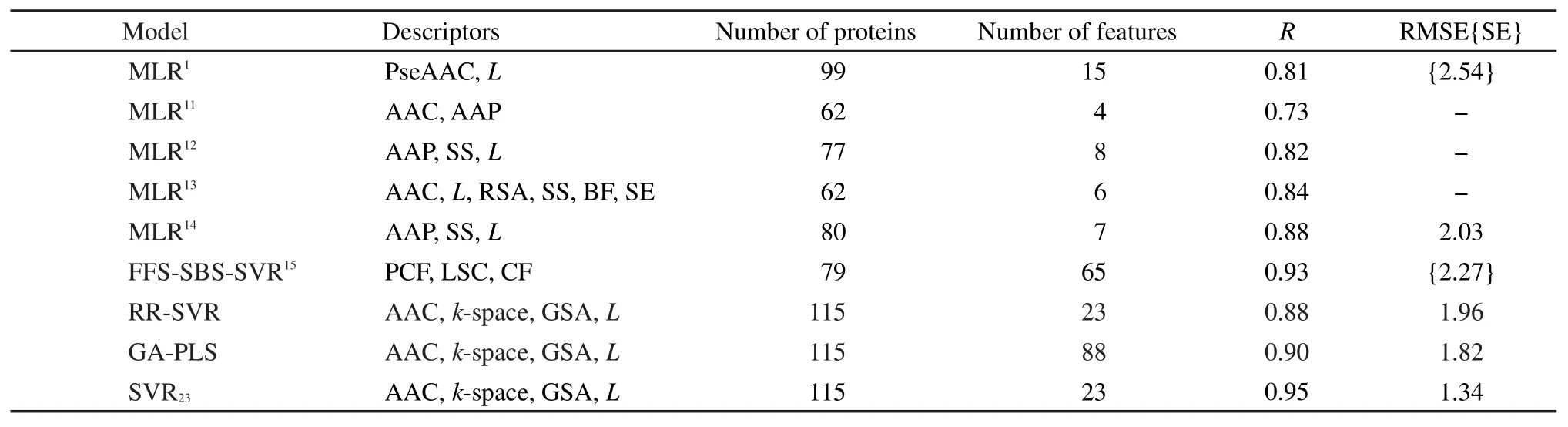
表3 Jackknife交叉验证结果比较Table 3 Comparison of Jackknife cross-validation results

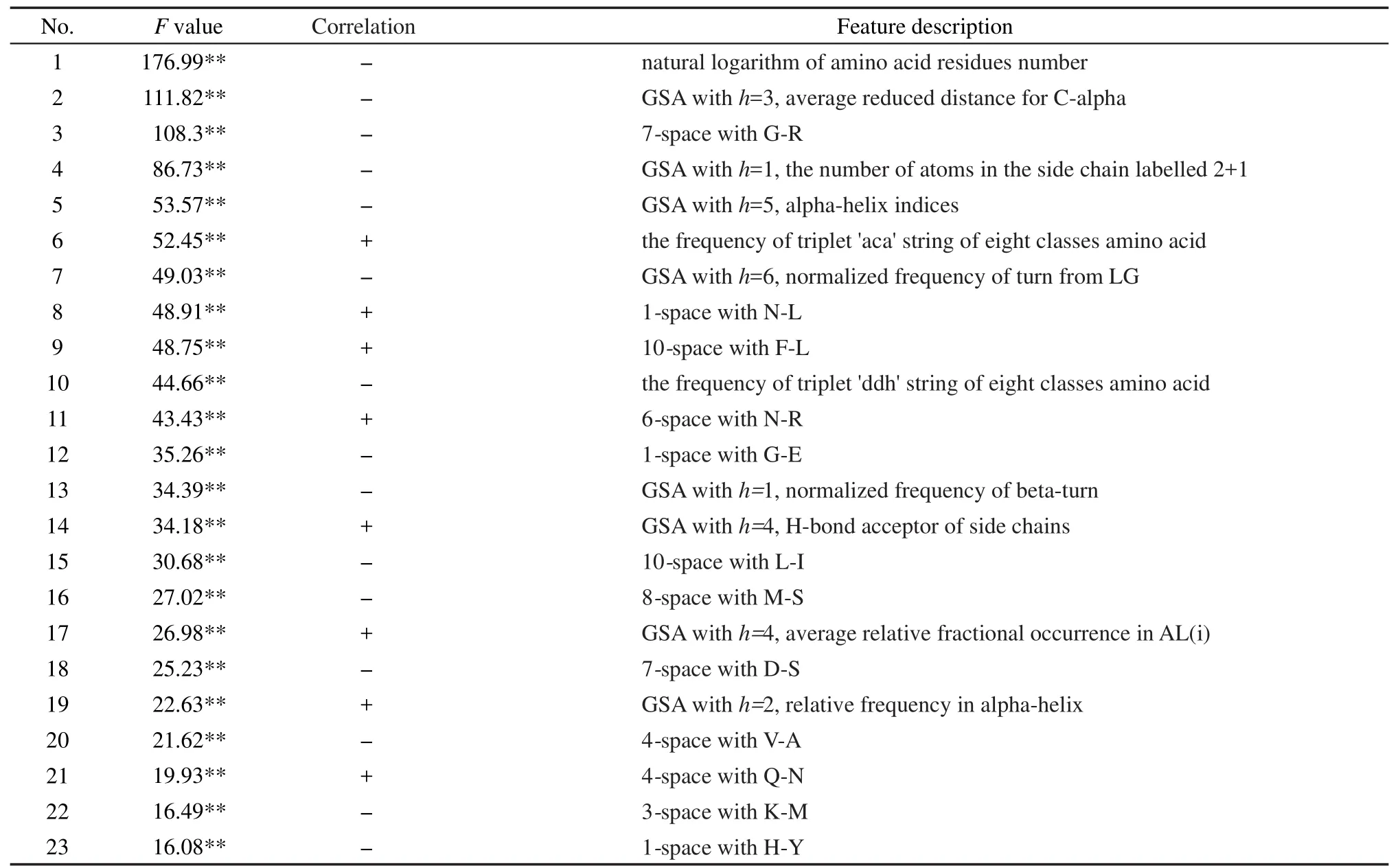
表4 筛选后保留的23个特征Table 4 23 retained features after feature screening

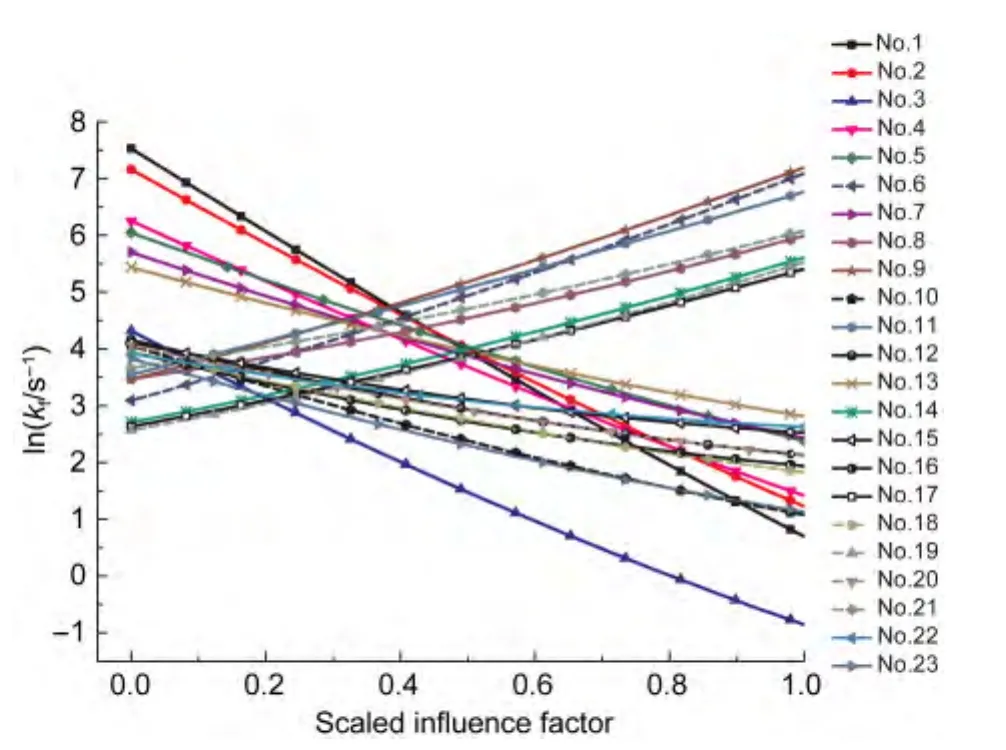
图3 折叠速率相关的23个保留描述符的单因子效应Fig.3 Single-factor effects of 23 retained descriptors on protein folding rate

4 小结与讨论

包括多种组分、上下文关联与长度在内的9357个描述符较完整地表征了一条蛋白质序列,但其中存在大量与折叠速率无关或冗余的特征,经改进的BMSF非线性粗筛和多轮末尾淘汰精细筛选,保留了23个物化意义明确的特征,建立的SVR模型非线性回归极显著,获得了优于文献报道的留一法预测精度.单因子效应分析显示,23个保留描述符可明显分为三类:第一类与折叠速率负相关,包括序列长度和5个地统计学关联特征;第二类与折叠速率同样负相关,包括8个k-space特征和1个氨基酸分八类时的三联体特征;第三类与折叠速率正相关,包括1个氨基酸分八类时的三联体特征、4个kspace特征和3个地统计学关联特征.蛋白质折叠速率主要受序列长度、中短程关联特征、三联体残基组份特征等影响.

蛋白质折叠是一个非常复杂的过程,本文仅基于一级序列,未涉及蛋白质高级结构特征;折叠速率实验值取自不同文献,实验环境的差异如温度也未能考虑.本文结果存在进一步改进空间,同时需更多样本验证支持.

(1) Guo,J.X.;Rao,N.N.;Liu,G.X.;Li,J.;Wang,Y.H.Prog.Biochem.Biophys.2010,37(12),1331.[郭建秀,饶妮妮,刘广雄,李 杰,王云鹤.生物化学与生物物理进展,2010,37(12),1331.]

(2) Xi,L.L.;Li,S.Y.;Liu,H.X.;Li,J.Z.;Lei,B.L.;Yao,X.J.J.Theor.Biol.2010,264(4),1159.doi:10.1016/j.jtbi.2010.03.042

(3) Plaxco,K.W.;Simons,K.T.;Baker,D.J.Mol.Biol.1998,277(4),985.doi:10.1006/jmbi.1998.1645

(4) Ivankov,D.N.;Garbuzynskiy,S.O.;Alm,E.;Plaxco,K.W.;Baker,D.;Finkelstein,A.V.Protein Sci.2003,12(9),2057.doi:10.1110/ps.0302503

(5) Weikl,T.R.;Dill,K.A.J.Mol.Biol.2003,332(4),953.doi:10.1016/S0022-2836(03)00884-2

(6) Zhang,L.X.;Li,J.;Jiang,Z.T.;Xia,A.G.Polymer2003,44(5),1751.doi:10.1016/S0032-3861(03)00021-1

(7) Capriotti,E.;Casadio,R.Bioinformatics2007,23(3),385.doi:10.1093/bioinformatics/btl610

(8) Ivankov,D.N.;Bogatyreva,N.S.;Lobanov,M.Y.;Galzitskaya,O.V.PLoS One2009,4(8),e6476.

(9) Gong,H.P.;Isom,D.G.;Srinivasan,R.;Rose,G.D.J.Mol.Biol.2003,327(5),1149.doi:10.1016/S0022-2836(03)00211-0

(10) Ivankov,D.N.;Finkelstein,A.V.Proc.Natl.Acad.Sci.U.S.A.2004,101(24),8942.doi:10.1073/pnas.0402659101

(11) Ma,B.G.;Guo,J.X.;Zhang,H.Y.Proteins:Struct.,Funct.,Bioinf.2006,65(2),362.doi:10.1002/prot.21140

(12) Jiang,Y.F.;Iglinski,P.;Kurgan,L.J.Comput.Chem.2009,30(5),772.doi:10.1002/jcc.21096

(13) Gao,J.Z.;Zhang,T.;Zhang,H.;Shen,S.Y.;Ruan,J.S.;Kurgan,L.Proteins:Struct.,Funct.,Bioinf.2010,78(9),2114.

(14) Shen,H.B.;Song,J.N.;Chou,K.C.J.Biomed.Sci.Eng.2009,2(3),136.doi:10.4236/jbise.2009.23024

(15)Cheng,X.;Xiao,X.;Wu,Z.C.;Wang,P.;Lin,W.Z.Proteins:Struct.,Funct.,Bioinf.2013,81(1),140.doi:10.1002/prot.24171

(16)Zhang,H.Y.;Wang,H.Y.;Dai,Z.J.;Chen,M.S.;Yuan,Z.M.BMC Bioinformatics2012,13(1),298.doi:10.1186/1471-2105-13-298

(17)Han,N.;Yuan,Z.M.;Chen,Y.;Dai,Z.J.;Wang,Z.M.Acta Phys.-Chim.Sin.2013,29(9),1945.[韩 娜,袁哲明,陈 渊,代志军,王志明.物理化学学报,2013,29(9),1945.]doi:10.3866/PKU.WHXB201306182

(18)Guo,J.X.;Rao,N.N.;Liu,G.X.;Yang,Y.;Wang,G.J.Comput.Chem.2011,32(8),1612.doi:10.1002/jcc.21740

(19) Galzitskaya,O.V.;Garbuzynskiy,S.O.;Ivankov,D.N.;Finkelstein,A.V.Proteins:Struct.,Funct.,Genet.2003,51(2),162.doi:10.1002/prot.10343

(20) Kawashima,S.;Pokarowski,P.;Pokarowska,M.;Kolinski,A.;Katayama,T.;Kanehisa,M.Nucl.Acids Res.2008,36(suppl.1),D202.

(21) Gromiha,M,M.;Selvaraj,S.Prep.Biochem.Biotechnol.1999,29(4),339.doi:10.1080/10826069908544933

(22) Zhou,P.;Tian,F.F.;Li,B.;Wu,S.R.;Li,Z.L.Acta Chim.Sin.2006,64(7),691.[周 鹏,田菲菲,李 波,吴世容,李志良.化学学报,2006,64(7),691.]

(23)Tan,X.S.;Wang,Z.M.;Tan,S.Q.;Yuan,Z.M.;Xiong,X.Y.J.Syst.Simul.2009,21(24),7795.[谭显胜,王志明,谭泗桥,袁哲明,熊兴耀.系统仿真学报,2009,21(24),7795.]

(24) Dai,Z.J.;Zhou,W.;Yuan,Z.M.Acta Phys.-Chim.Sin.2011,27(7),1654.[代志军,周 玮,袁哲明.物理化学学报,2011,27(7),1654.]doi:10.3866/PKU.WHXB20110735

(25) Chang,C.C.;Lin,C.J.ACM TIST.2011,2(3),27.

(26)Chen,Y.;Yuan,Z.M.;Zhou,W.;Xiong,X.Y.Acta Phys.-Chim.Sin.2009,25(8),1587.[陈 渊,袁哲明,周 玮,熊兴耀.物理化学学报,2009,25(8),1587.]doi:10.3866/PKU.WHXB20090752

(27) Leardi,R.J.Chemometr.2000,14(5-6),643.doi:10.1002/1099-128X(200009/12)14:5/6<643::AID-CEM621>3.0.CO;2-E

(28)Wang,Z.M.;Han,N.;Yuan,Z.M.;Wu,Z.H.Acta Phys.-Chim.Sin.2013,29(3),498.[王志明,韩 娜,袁哲明,伍朝华.物理化学学报,2013,29(3),498.]doi:10.3866/PKU.WHXB201301042

(29) Ouyang,Z.;Liang,J.Protein Sci.2008,17(7),1256.doi:10.1110/ps.034660.108