随机利率下的脆弱期权定价

许艳红，薛红，王晓东

(西安工程大学理学院，陕西西安710048)

随机利率下的脆弱期权定价

许艳红，薛红，王晓东

(西安工程大学理学院，陕西西安710048)

以信用风险模型为基础，假定股票价格、公司价值和公司负债均服从几何分数布朗运动，利率满足由分数布朗运动驱动的Vasicek模型，建立了随机利率下脆弱期权定价数学模型.利用分数布朗运动随机分析理论和保险精算方法，推导出脆弱期权的定价公式.

分数布朗运动;随机利率;保险精算方法;脆弱期权

0 引言

脆弱期权是指含有信用风险的期权，Merton［1］首先建立了关于信用风险的结构化模型，结合相对于其负债公司资产价值模型推导违约风险价格，Johnson和Stulz［2］首次探讨了含有信用风险的期权的定价问题，Hull和White［3］通过构造一个二项格状图求得了脆弱期权的价格，Klein［4］假设信用风险与标的资产价值相关得到了脆弱期权的定价公式.在以往的期权定价研究中，人们普遍假设资产价格服从几何布朗运动，但是近年来大量的研究表明，资产收益率的分布具有“尖峰厚尾”的特征，股价变化也不是随机游走，而是呈现不同程度的相关性，分数布朗运动恰好具有这些优点，因此用分数布朗运动来刻画资产价格的变化，更符合市场的实际情况.黄玲君、周圣武［5］等在公司负债为常数的条件下给出了股价服从分数布朗运动的脆弱欧式期权定价公式，潘坚［6］利用偏微分方程方法给出了分数布朗运动下脆弱欧式期权的定价公式.同时，在以往的期权定价模型中，一个重要的假设是利率为常数，然而，在现实市场中，利率在一段时间内常常表现出一定的随机性.很多学者对此进行了大量的相关研究，周海林［7］等给出了随机利率条件下的欧式期权定价，薛红［8］在利率满足由分数布朗运动驱动的Hull-White模型下给出了可转换债券的定价公式.

1998 年Mogens Bladt等［9］首次提出期权定价的保险精算方法，该方法将期权定价问题转化为等价的公平保费问题.本文假定股票价格、公司价值和公司负债均服从几何分数布朗运动，利率满足由分数布朗运动驱动的Vasicek模型，利用分数布朗运动随机分析理论和保险精算方法给出了脆弱期权的定价公式.

1 金融市场数学模型

假设股票价格为S(t)，公司资产市场价值为V(t)，公司负债为D(t).设X(T)为公司在T时刻承诺支付给债权人的金额，若公司自始至终都具有清偿能力，那么公司的债权人在T时刻取得偿付额X(T).若在T时刻V(T)＜D(T)，则发生违约，此时公司的债权人取得的偿付额就是X′(T)=X(T)V(T)/D(T)，则在T时刻，公司的实际支付额可以表示为

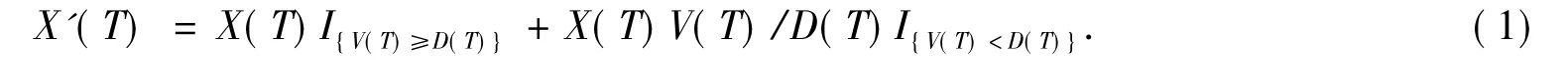
假定股票价格S(t)，公司价值V(t)，公司负债D(t)和利率r(t)分别满足随机微分方程

2 脆弱期权的定价

定义1［12］随机过程{S(t)，t≥0}在［0，T］上的期望收益率β(u)定义为

引理2［12］随机过程{S(t)，t≥0}在［0，T］上的期望收益率βS(u)满足βS(u)=μS，公司价值{V(t)，t≥0}和公司负债{D(t)，t≥0}在［0，T］上的期望收益率βV(u)，βD(u)分别满足βV(u)=μV，βD(u)=μD.

定义2在到期日T时刻，承诺支付额为X(T)=(S(T)-K)+，而出现违约或破产时的实际支付额为X(T)=(V(T)/D(T))(S(T)-K)+的脆弱看涨期权的保险精算价格定义为

其中股票价格S(T)，公司价值V(T)和公司负债D(T)分别用期望收益率βS(u)，βV(u)，βD(u)贴现，执行价格K用随机利率r(s)贴现.

定理2在到期日T时刻，承诺支付额为X(T)=(S(T)-K)+而出现违约或破产时的实际支付额为X(T)=(V(T)/D(T))(S(T)-K)+的脆弱看涨期权的价格为

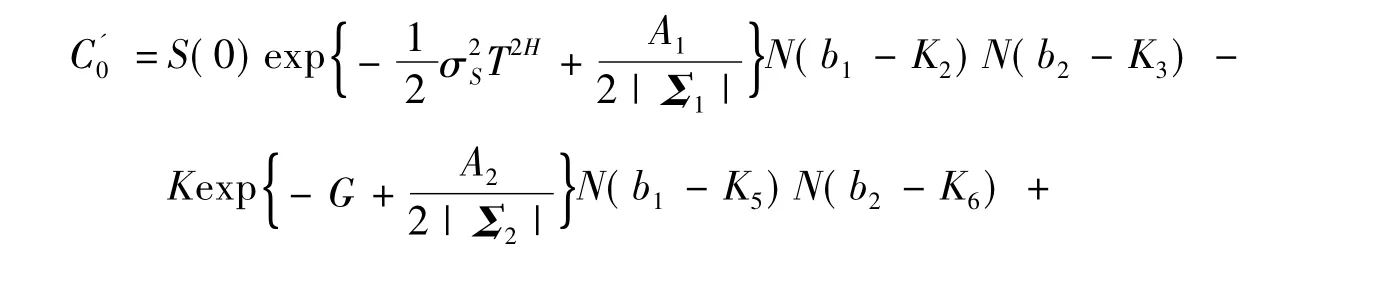
结合式(12)～(15)即可得式(11).

推论1当b=0，σr=0，a→0且σD→0时，可得分数布朗运动下的脆弱期权定价公式，与文献［5］结果一致.

推论2当b=0，σr=0，a→0且H=1/2时，可简化为文献［4］中的结果.

推论3当b=0，σr=0，a→0，H=1/2，且σD→0时，则退化为文献［2］中的结果.

［1］MERTON R.On the pricing of corporate debt：The risk structure of interest rates［J］.Journal of Finance，1974，29(2)：449-470.

［2］JOHNSON H，STULZ R.The pricing of options under default risk［J］.Journal of Finance，1987，42(2)：267-280.

［3］HULL J M，WHITE A.The impact of default risk on the prices of options and other derivative securities［J］.Journal of Banking＆Finance，1995，19(2)：299-323.

［4］KLEIN P.Pricing Black-Scholes options with correlated credit risk［J］.Journal of Banking and Finance，1996，20(7)：1121-1129.

［5］黄玲君，周圣武.股价服从分数布朗运动的脆弱欧式期权定价［J］.云南大学学报：自然科学版，2010，32(2)：109-112.

［6］潘坚.分数次布朗运动下脆弱欧式期权定价的新解法［J］.赣南师范学院学报，2011，33(3)：14-18.

［7］周海林，吴鑫育，高凌云.随机利率条件下的欧式期权定价［J］.系统工程理论与实践，2011，31(4)：729-734.

［8］薛红，李军，吴晓蕊.随机利率下可转换债券定价［J］.西安工程大学学报，2011，25(1)：119-121.

［9］BLADT M，RYDBERG H T.An actuarial approach to option pricing under the physical measure and without market assumptions［J］.Insurance：Mathematics and Economics，1998，22(1)：65-73.

［10］GUASONI P.No arbitrage under transaction costs with fractional Brownian motion and beyond［J］.Mathematical Finance，2006，16(3)：569-582.

［11］BIAGINI F，HU Y，OKSENDALl B，et al.Stochastic calculus for fractional Brownian notion and applications［M］.New York： Springer，2008.

［12］XUE H，LU J，WANG X.Swap option pricing model in fractional jump-diffusion environment［C］//Proceedings 2011 World Congress on Engineering and Technology，Shanghai，China，2011：336-339.

Vulnerable option pricing under stochastic interest rate

XU Yan-hong，XUE Hong，WANG Xiao-dong

(School of Science，Xi'an Polytechnic University，Xi'an 710048，China)

Based on the credit risk model，assume that stock price，corporate value and corporate debt obey the geometric fractional Brownian motion，interest rate satisfies the Vasicek model driven by fractional Brownian motion.The vulnerable option pricing mathematic model under stochastic interest rate is built，the pricing formulae for vulnerable option is obtained by fractional Brownian motion stochastic analysis theory and the actuarial approach.

fractional Brownian motion;stochastic interest rate;actuarial approach;vulnerable option

1674-649X(2014)01-0133-07

F 830.9;O 211.6

A

编辑、校对：武晖

2013-06-21

陕西省教育厅自然科学专项基金项目(12JK0862)

薛红(1964-)，男，山西省万荣县人，西安工程大学教授，博士.E-mail：xuehonghong@sohu.com