实值信息系统上基于熵的属性约简
鲁文霞,马盈仓
(西安工程大学理学院,陕西西安710048)
实值信息系统上基于熵的属性约简
鲁文霞,马盈仓
(西安工程大学理学院,陕西西安710048)
研究实值系统中的知识获取是粒计算研究的主要方向之一.为给出一种高效的知识获取方法,文中基于邻域粗糙集的原理,针对实值特点,在实值信息系统上给出熵和基于熵的属性重要度的定义和约简定理.同时研究其性质,并给出了实值信息系统上基于熵的属性重要度的约简算法,对算法的性质进行了分析,通过实例验证了该算法的有效性.
粗糙集理论;实值系统;属性约简;熵
0 引言
粗糙集作为一种处理不协调、不确定与不完备数据的新的数学理论[1-2],最初是由波兰科学家Pawlak于1982年提出的.近几年来,它已经成功地应用于机器学习、模式识别、决策支持、数据挖掘、过程控制等领域[3-5].
然而经典粗糙集理论是基于等价关系的,分类过于苛刻,它适用于处理离散型变量,对于现实中广泛存在的数值型数据却不能直接处理.在金融、医疗、科研和工程领域,实值型变量无处不在,如:配电系统诊断的电流信号[6]等.为了解决这种问题,人们在经典粗糙集的基础上进行了许多有意义的推广,引入了很多新的模型,如模糊粗糙集模型[7-10]、邻域系统粗糙集模型[11]和邻域关系模型[12].其中,在邻域模型方面,Hu提出基于邻域粒化和粗糙逼近的数值属性约简[12],Yao[13]提出1-step邻域,Wu[14]提出并研究了k-step邻域信息系统的性质,以及带有误差范围和测试代价的数据属性约简[15]等.可以看出,不同的模型是基于不同的粒化和逼近机制来处理现实中实值型数据.
粗糙集理论中的约简一直是核心问题.合理的属性约简可以起到非常有效的作用,对于知识获取、决策分析等起到指导作用.一般地讲,一个决策系统的属性约简往往不是惟一的,理想中人们期望找到决策系统中的最小约简,但是找到最小约简是一个NP-hard的问题,所以在现实生活中人们解决这一类问题一般采取启发式算法来求出最优或次最优约简.在经典粗糙集模型上,借助熵及条件熵作为度量可以对属性进行约简[16].在实值系统上也有人在这方面作了文章,如:协调覆盖决策系统下基于条件信息熵的属性约简[17],覆盖决策信息系统的约简[18],模糊概率近似空间及其信息度量[19]等.本文在经典粗糙集熵的定义和邻域粗糙集模型研究的基础上,提出了实值信息系统上的熵和基于熵的属性重要度的定义,它是等价关系上一个推广,并研究了其性质.在实值信息系统上,给出了在熵定义下的约简定理,提出了基于熵的属性重要度约简算法,同时对算法的性质进行了理论分析,揭示了属性重要度作为启发式算法的合理性;最后通过实例,表明该算法是有效的.
1 邻域覆盖粗糙集
定义1[11]给定一个n维的实数空间Ω,ΔRN×RN→R,称Δ是RN上的一个度量,如果Δ满足:

则称〈Ω,Δ〉为度量空间.欧式距离是实数空间上常用的度量.
定义2实值信息系统S=(U,A),xi∈U,a∈A,xi的关于属性a的e-邻域为
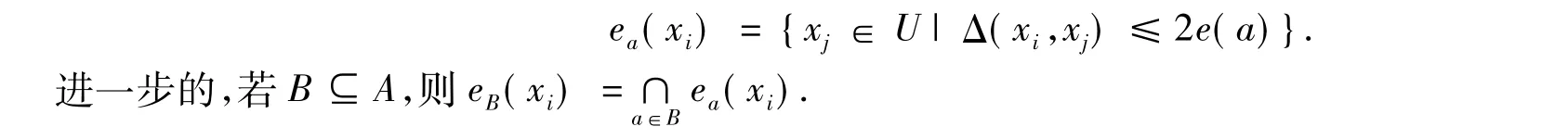
注e(a)为误差范围.
根据度量的性质,有如下结论:
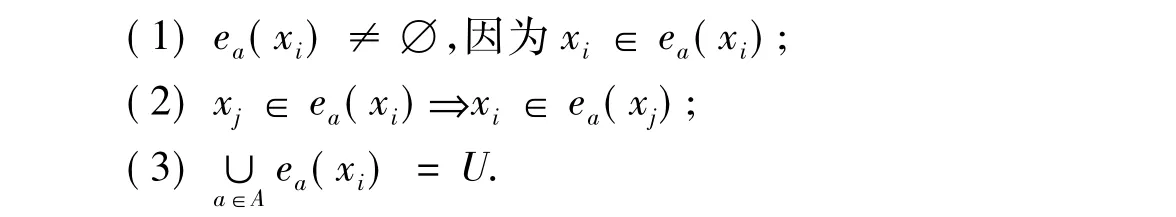
不难看出,邻域粒子族{ea(xi)|i=1,2,…,n}构成了U的一个覆盖.
进一步的,由邻域的定义,可以得到
性质1(1)eB1∪B2=eB1∩eB2,(2)∀xi∈U,e1≤e2,则e1(xi)⊆e2(xi).
2 实值信息系统中基于熵的约简
2.1 邻域下的熵
定义3实值信息系统S=(U,A),xi∈U,B⊆A,则属性集B具有的信息熵定义为

其中|U|表示论域中元素的个数,|eB(xi)|/|U|表示xi的B邻域在U中的概率.
注此定义是经典粗糙集中熵的一种推广,可以退化为等价关系中定义的熵.
定理1实值信息系统S=(U,A),xi∈U,B⊆A,则H(B)≤H(A).
证明由于

由邻域的定义B⊆A,则

2.2 邻域下的属性重要性的度量
定义4实值信息系统S=(U,A),xi∈U,a∈A,属性a在A中的重要性定义为

特别当A={a}时,用sig(a)表示sigØ(a):
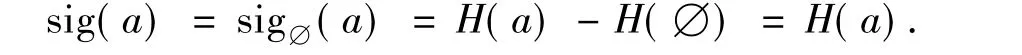
定义5实值信息系统S=(U,A),a∈A,若H(A)≠H(A-{a}),则称属性a在A中是必要的,否则就是不必要的.
性质2(1)0≤sigA-{a}(a)≤1;(2)属性a∈A在A中是必要的充要条件是sigA-{a}(a)>0;(3) CORE(A)={a∈A|sigA-{a}(a)>0}.
证明(1)由定理1的结论可知,0≤sigA-{a}(a)≤1.
(2)充分性:若a∈A在A中是必要的,则H(A)≠H(A-{a}).而H(A)≥H(A-{a}),故sigA-{a}(a)>0.
必要性:若sigA-{a}(a)>0,即H(A)≠H(A-{a}),故a∈A在A中是必要的.
(3)由性质(2)可知.
定义6实值信息系统S=(U,A),xi∈U,B⊆A,任意属性a∈A-B关于属性集B中的重要性定义为

通过信息系统属性约简的概念和以上结论,可以容易地得到如下定理,它通过熵来刻画信息系统约简.
定理2实值信息系统S=(U,A),B⊆A,如果:(1)H(A)=H(B),(2)∀a∈B,有sigB-{a}(a)>0,则B为A的一个约简.
证明在实值信息系统中B⊆A为A的一个约简的充分必要条件为eA(xi)=eB(xi)且B是独立的.
由定理1知,当B⊆A时,eA(xi)=eB(xi)成立的充分必要条件是H(A)=H(B).B是独立的成立的充分必要条件是∀a∈B是必要的,则H(B)≠H(B-{a}),即sigB-{a}(a)>0.故定理成立.
2.3 属性重要性的约简算法
由于核属性是所有约简的交集,因此,在求最小约简时可以把核作为起点,在性质2中可以很容易地求出属性集的核.再根据定义4中定义的属性重要度作为启发式函数,选择重要度最大的属性添加到核中去,直到熵等于整个条件属性的熵为止.
实值信息系统的核与约简算法:
输入:实值信息系统S=(U,A),其中U为论域,A为条件属性.
输出:该信息系统的核和约简.
步骤1求CORE(A),计算每个属性a∈A在A中是否必要,且令CORE(A)=Ø.若sigA-{a}(a)>0,则CORE(A):=CORE(A)∪{a},最后得到的CORE(A)为属性集A的核;若H(A)=H(CORE(A))则终止(此时CORE(A)为A的最小约简);否则,执行步骤2.
步骤2令C=CORE(A),对属性集A-C重复执行:当C=Ø时,计算每一个属性a∈A的熵H({a}),若H({a})=H(A),则终止(此时{a}为A的最小约简);当C≠Ø时,转以下步骤:
(1)对每个属性a∈A-C,计算sigC(a).
(3)若H(C)=H(A),则终止(此时C为A的最小约简);否则,转(1).
以上是依据熵的属性重要度求属性约简的算法步骤,该算法是有效的,下面通过例子进行分析.
例1实值信息系统S=(U,A),如表1,其中U={x1,x2,x3,x4,x5},A={a1,a2,a3},求其信息表的核与约简.其中,Δ(x1,x2)=|a(xi)-a(xj)|.
步骤1由于


表1 信息表
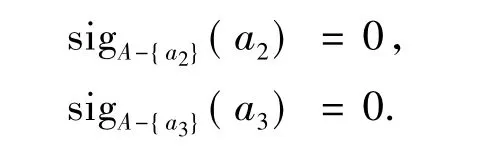
故A中必要元素为a1,即CORE(A)={a1}.
步骤2令C={a},对属性a2,a3∈A-C,计算sigC(a2),sigC(a3).

若选择属性a2,C:=C∪{a2},则H(C)=H(A),终止.
若选择属性a3,C:=C∪{a3},则H(C)=H(A),终止.
所给算法求出信息系统的核CORE(A)={a1};约简为{a1,a2}或{a1,a3}.
3 结束语
本文在邻域覆盖粗糙集的定义下,将经典粗糙集中的熵和属性重要度推广到实值信息系统中,给出了其在实值系统上的定义,并给出了实值信息系统在熵下的约简定理.在此基础上,提出了一种基于熵的属性重要度的实值信息系统上的属性约简算法,并通过例子验证了该算法的有效性.今后将对实值决策系统在条件熵上的属性约简进行研究,并将其应用到UCI数据中,与其他算法进行比较.
[1]PAWLAK Zdzislaw.Rough sets[J].International Journal of Computer and Information Sciences,1982,11(5):341-356.
[2]张文修,吴伟志,梁吉业,等.粗糙集理论与方法[M].北京:科学出版社,2005:1-15.
[3]朱永利,吴立增,李雪玉.贝叶斯分类器与粗糙集相结合的变压器综合故障[J].中国电机工程学报,2005,25(10):159-165.
[4]孙秋野,张化光.基于粗糙集的配电系统连续信号故障诊断方法[J].中国电机工程学报,2006,26(11):156-161.
[5]刘清,刘少辉,郑非.Rough逻辑及其在数据约简中的应用[J].软件学报,2001,12(3):415-419.
[6]SNN Q Y,ZHANG H G.Fault diagnose algorithm of distribution system by continuous signals based on rough sets[J].The Chinese Society for Electrical Engineering,2006,26(11):156-161.
[7]罗承忠.模糊集引论[M].北京:北京师范大学出版社,2007:45-48.
[8]高新波.模糊聚类分析及其应用[M].西安:西安电子科技大学出版社,2004:44-45.
[9]SLAVKA B.Approximation of fuzzy concepts in decision making[J].Fuzzy Sets and Systems,1997,85(2):23-29.
[10]RADZIKOWSKA M,KERRE E E.Comparative study of fuzzy rough sets[J].Fuzzy Sets and System,2002,126(2):29-34.
[11]HU Qinghua,ZHANG Lei,CHEN Degang.Gaussian kernel based fuzzy rough sets:Model,measures and applications[J].International Journal of Approximate Reasoning,2010,51(1):453-471.
[12]胡清华,于达仁,谢宗霞.基于邻域粒化和粗糙逼近的数值属性约简[J].软件学报,2008,19(3):640-649.
[13]YAO Y.Y.Relational interpretation of neighborhood operators and rough set approximation operators[J].Information Science,1998,111(1):239-259.
[14]WU Weizhi,ZHANG Wenxiu.Neighborhood operator systems and approximations[J].Information Science,2002,144(1-4): 201-217.
[15]MIN Fan,ZHU William.Attribute reduction of data with error ranges and test costs[J].Information Science,2012,18(4):3-14.
[16]张海军,梁吉业,梁春华.一种基于知识量的约简算法[J].小型微型计算机系统,2007,28(11):1968-1971.
[17]夏秀云,秦克云,田浩.协调覆盖决策系统下基于条件信息熵的属性约简[J].河南大学学报:自然科学版,2010,40 (4):406-410.
[18]许晴媛,李进金,张燕兰.覆盖决策信息系统的约简[J].山东大学学报:理学版,2010,45(1):89-93.
[19]HU Qinghua,YU Daren,XIE Zongxia,et al.Fuzzy probabilistic approximation spaces and their information measures[J].IEEE Transactions on Fuzzy Systems,2006,14(2):191-201.
Attribute reduction of the real value information system based on entropy
LU Wen-xia,MA Ying-cang
(School of Science,Xi'an Polytechnic University,Xi'an 710048,China)
Research knowledge acquisition of the real value system is one of the main directions of the granular computing research.For giving an efficient knowledge acquisition method,based on the neighborhood of rough set theory and according to the characteristics of the real value,the definition of the entropy and attribute importance based on the entropy and reduction theorem in the real value information system are given,and its properties are studied.Moreover,the algorithm of attribute reduction based on attribute importance in the real value information system is proposed.Lastly,the properties of algorithm are discussed and the effectiveness of the algorithm are showed by an example.
rough set theory;real system;attribute reduction;entropy
TP 18;B 815
A
1674-649X(2014)01-0128-05
编辑、校对:武晖
2013-07-04
国家自然科学基金资助项目(61170128);陕西省教育厅专项科研计划项目(12JK0878);西安工程大学研究生创新基金资助(chx131114)
马盈仓(1972-),男,陕西省合阳县人,西安工程大学教授,博士,主要研究领域为粗糙集理论及应用、非经典数理逻辑.E-mail:mayingcang@126.com

