基于高频数据的股指期货动态价量关系研究

林祥友 甘雨婕

(成都理工大学商学院，四川 成都 610059)

一、引言

我国资本市场于2010年4月16日正式推出沪深300股指期货。股指期货市场的交易者要想在股指期货市场上取得交易策略的成功，第一需要正确判断股指期货市场的价格运动趋势，第二需要正确把握股指期货市场的价格波动大小，第三需要正确分析股指期货市场的价格收益率、波动率同成交量、持仓量之间的动态价量关系，据以正确分析股指期货合约的运行规律。因此，围绕我国股指期货市场的价(收益率和波动率)与量(成交量和持仓量)之间的复杂关系的相关研究便成为股指期货市场理论界和实务界迫切而重要的研究课题。

Karpoff(1987)[1]曾经指出，研究价格波动与交易量关系有助于了解市场的结构、市场信息传播的方式和速度，以及市场价格如何对信息做出反映。国内外学者对金融资产(包括股票和期货等)的价量关系进行大量有益的研究，但研究结论并不统一。一类观点是期货价量之间存在密切关系。Karpoff(1987)[1]、Cornell(1981)[2]、Grammatikos & Saunders(1986)[3]、Foster(1995)[4]等采用不同的方法，对不同期货的价格波动与交易量的关系进行实证研究发现，期货价格波动与交易量之间是正相关关系。Lamoureux和Lastrape(1990)[5]将交易量作为信息流的替代指标引入到GARCH模型的条件方差方程中，发现交易量是由产生价格波动的相同因素驱动的，说明交易量对价格波动具有很强的解释能力。Bessembinder和Seguin(1993)[6]将持仓量作为市场深度的替代变量，将成交量和持仓量分解为可预期部分和不可预期部分，研究成交量和持仓量对期货价格波动性的影响。结果显示，成交量和持仓量对期货价格波动均有显著的影响，可预期成交量和不可预期成交量对期货价格波动具有正向影响，不可预期成交量对期货价格波动的影响比可预期成交量对期货价格波动的影响要大许多。Ragunathan和Peker(1997)[7]利用同样的方法对澳大利亚悉尼期货交易所四个金融期货品种的价格波动、成交量和持仓量之间的关系进行了实证研究，得出类似的结论。Girma(2002)[8]研究了期货价差波动、交易量与持仓量的关系，发现交易量和持仓量对价格波动具有较强的解释力。Marsh与Wagner(2004)[9]使用GARCH-M模型对国际市场的量价关系进行分析，发现成交量能够解释市场波动的GARCH效应。Mubarik和Javid(2009)[10]将成交量加入GARCH-M模型中，结果表明成交量与收益率是当前收益率的重要解释变量。另一类观点是期货价量关系并不明显。McCarthy和Najand(1993)[11]对外汇期货市场的研究发现，期货价格收益与交易量之间不存在相关关系。Nowbutsing和Naregadu(2009)[12]对成交量、收益率与波动率三者之间的关系进行研究发现，成交量与波动率之间的关系并不明显。

国内学者也对期货价量关系进行了大量研究，华仁海等(2002)[13]利用相关分析、VAR模型和Granger因果检验对我国期货市场价格波动与成交量之间的关系进行了实证分析，结果表明交易量与绝对价格波动之间存在正相关，而与价格波动之间不相关。华仁海、仲伟俊(2002)[14]以上海期货交易所的金属铜为例，利用GARCH模型讨论期货价格与交易量之间的相互关系，得出了交易量的变化值即相对交易量与期货价格之间的关系。华仁海，仲伟俊(2003)[15]对我国期货市场铜、铝、大豆期货的价格收益、交易量、波动性之间的关系进行动态分析，得到的结论是期货价格收益与交易量之间不存在相关关系，期货价格上升和下降过程的交易量是对称的，期货价格的绝对收益与交易量之间存在正相关关系。周志明、唐元虎、施丽华(2004)[16]对期铜和期铝两个期货合约收益率波动的研究表明：交易量与收益率波动之间的关系是正相关，持仓量与收益率波动之间的关系是负相关。华仁海和仲伟俊(2004)[17]借助GARCH模型，分两种情况研究成交量和持仓量对股指期货价格波动的影响，对我国期货市场期货价格波动与成交量和空盘量之间的动态关系进行了实证研究。田新民，沈小刚(2005)[18]考察了交易量与持仓量对日内价格波动的影响，同时对预期和未预期交易量、持仓量对价格波动的影响进行了量化分析。结果发现：交易量与日内价格波动之间存在正相关关系，持仓量与日内价格波动之间存在负相关关系，未预期交易量对价格波动的影响比预期交易量大；未预期持仓量对价格波动的影响比预期持仓量大。翟光磊(2011)[19]通过对橡胶期货的量价关系实证分析得出结论：我国橡胶期货收盘价、成交量和持仓量具有长期稳定的均衡关系，收盘价是持仓量变化的格兰杰原因，持仓量变化是成交量变化的格兰杰原因，成交量变化是收盘价变化的格兰杰原因。

在对期货价量关系的研究中，研究对象主要集中在商品期货市场，股指期货市场的相关研究相对较少。研究视角主要包括收益率、绝对收益率、价格波动与成交量之间的关系，收益率、绝对收益率、价格波动与持仓量之间关系的研究相对较少。对于研究区间，划分股指期货合约的主力合约期和非主力合约期的价量关系的相关研究还没有出现。对于研究数据，大多数学者针对每日收盘数据进行研究，损失了大量信息，未能有效捕捉到买卖双方的日内信息，利用日内高频数据进行价量分析的文献也比较少。本文在借鉴期货价量关系的现有研究成果的基础上，区分股指期货的主力合约期和非主力合约期，区分价格收益率和绝对收益率，区分成交量、持仓量和相对成交量、相对持仓量，区分预期成交量和未预期成交量，预期持仓量和未预期持仓量，利用股指期货的5分钟高频数据，全面研究股指期货的价(收益率和波动率)与量(成交量和持仓量)之间的动态关系。

二、数据与模型

在股指期货价量关系的研究中，股指期货的主力合约期和非主力合约期的价量关系可能存在差异，故本文分别收集了股指期货合约IF1111在主力合约转换日(2011年10月19日)前的非主力合约期15个交易日和主力合约转换日后的主力合约期20个交易日的五分钟的价格(包括开盘价、最高价、最低价、收盘价)和数量(包括成交量和持仓量)的高频交易数据，并进行了时间配对处理和对数化处理，作为后文实证研究的数据基础。股指期货合约的高频交易数据全部来自交易开拓者行情系统。

(一)相关指标定义

由股指期货五分钟收盘价序列可以得到对应的五分钟价格收益率序列和绝对收益率序列，为了克服五分钟内股指期货价格收益率数据较小给数据处理带来的困难，本文将股指期货的价格收益率和绝对收益率进行如下定义。

股指期货的价格收益率

Rt=(LnPt-LnPt-1)×100

(1)

股指期货的绝对收益率

|Rt|=|LnRt-LnPt-1|×100

(2)

式(1)、(2)中LnPt为股指期货五分钟收盘价格的自然对数。

股指期货的价格波动率

Garman和Klass(1980)提出关于股市日内波动率衡量的优化方法，这一方法被认为是最小方差的无偏估计，它同时考虑了开盘价、收盘价、最高价、最低价，在相对效率上比仅考虑收盘价的传统方法提高很多。张孝岩，沈中华(2011)[20]采用此方法测算了我国股指期货的GK波动率，并说明其在高频数据中的适用性。本文借鉴此方法估算股指期货的五分钟内高频价格波动率。股指期货的价格波动率的估计值为

(3)

式(3)中的u=Ht-Ot为正则化最高价；d=Lt-Ot为正则化最低价；c=Ct-Ot为正则化收盘价。Ht为最高价，Lt为最低价，Ot为开盘价，Ct为收盘价。

股指期货的成交量

LnTVt=Ln(TVt)

(4)

股指期货的持仓量

LnOIt=LN(OIt)

(5)

股指期货的相对成交量

LTVt=(LnTVt-LnTVt-1)×100

(6)

股指期货的相对持仓量

LOIt=(LnOIt-LnOIt-1)×100

(7)

式(4)、(5)、(6)、(7)中，TVt为成交量的原始数据，OIt为持仓量的原始数据。

(二)股指期货合约收益率与成交量、持仓量之间关系的检验模型

在检验股指期货合约的收益率(包括价格收益率和绝对收益率)与成交量(相对成交量)、持仓量(相对持仓量)之间的关系时，利用格兰杰因果检验确定价格收益率与成交量(相对成交量)、持仓量(相对持仓量)，绝对收益率与成交量(相对成交量)、持仓量(相对持仓量)之间的因果关系。

价格收益率与成交量之间的格兰杰因果检验需要估计以下回归式：

(8)

(9)

如果对式(8)的滞后LnTV所估计的系数集在统计上是异于零的(即∑αi≠0)；并且对式(9)中的滞后R所估计的系数集不是统计上异于零的(即∑δj=0)，则表明有从LnTV到R的单向因果关系。如果对式(8)的滞后LnTV所估计的系数集不是在统计上异于零的(即∑αi=0)；并且对式(9)中的滞后R所估计的系数集是统计上异于零的(即∑δj≠0)，则表明有从R到LnTV的单向因果关系。如果LnTV和R的系数集在两个回归中都是统计上异于零的，即∑αi≠0且∑δj≠0，则LnTV和R存在双向因果关系。如果LnTV和R的系数集在两个回归中都不是统计上显著异于零的，则LnTV和R不存在因果关系。

价格收益率与相对成交量、价格收益率与持仓量(相对持仓量)、绝对收益率与成交量(相对成交量)、绝对收益率与持仓量(相对持仓量)之间的因果关系检验的原理同上式(8)、(9)类似。

(三)股指期货合约波动率与成交量、持仓量之间关系的检验模型

考察沪深300股指期货日内五分钟价格波动率与成交量、持仓量之间的关系时，借鉴Bessembinder和Seguin(1993)的方法，建立如下模型1：

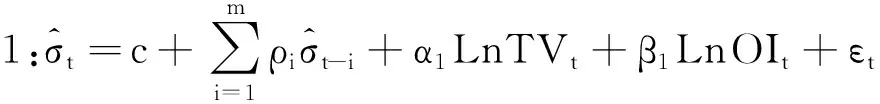
(10)

考察股指期货的波动率与预期成交量和未预期成交量，预期持仓量和未预期持仓量的关系差异，对波动率滞后项，预期成交量和未预期成交量，预期持仓量和未预期持仓量进行回归，建立模型2：

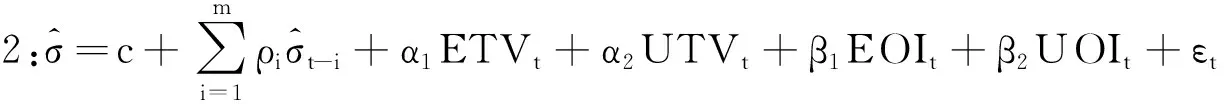
(11)

考察股指期货正的成交量冲击和负的成交量冲击对价格波动的影响差异，正的持仓量冲击和负的持仓量冲击对价格波动的影响差异时，在模型(2)的基础上加入虚拟变量D1和D2，建立模型3：

模型3：

(12)

式(11)、(12)中，ETVt为预期成交量，UTVt为未预期成交量，EOIt为预期持仓量，UOIt为未预期持仓量，D1为虚拟变量(UTVt>时，D1=1；否则D1=0)，D2为虚拟变量(UOIt>0时，D2=1；否则D2=0)。

在式(11)中，由于股指期货合约的成交量和持仓量呈高度序列相关，成交量和持仓量可通过ARIMA模型进行预报。在分析预期的成交量和持仓量，未预期的成交量和持仓量对波动性的不同影响时，需要利用ARIMA(p，d，q)模型对其进行分解，预期值由ARIMA模型的拟合值得到，未预期值就是实际值减去拟合值之差。ARIMA(p，d，q)模型估计中，滞后项数的选择基于AIC和SC准则。用此方法确定预期成交量ETVt，未预期成交量UTVt，预期持仓量EOIt，未预期持仓量UOIt，然后代入模型2进行估计。

在式(12)中，由于成交量的不同冲击对金融市场的波动有不同的影响，Bessembinder和Seguin(1993)发现正的成交量冲击对波动的影响比负的冲击更大，持仓量的不同冲击对金融市场的波动也是这样。因此，在对未预期的成交量和未预期的持仓量进行考察时，在模型3中引入了虚拟变量D1和D2，以分析正的和负的成交量冲击、正的和负的持仓量冲击对价格波动的不同影响。

三、实证分析

(一)股指期货合约价格数量指标的描述性统计

在对股指期货合约的价量关系进行实证分析之前，首先根据股指期货合约IF1111在非主力合约期的15个交易日，在主力合约期的20个交易日的五分钟原始价量数据，计算收益率、波动率、相对成交量、相对持仓量等研究变量。每个交易日有54个原始数据，非主力合约期共有810个原始数据，主力合约期共有1080个原始数据，由于计算股指期货的价格收益率、绝对收益率、相对成交量、相对持仓量等指标时需要对原始数据进行一阶差分，所以股指期货两个阶段所有指标的样本量分别为809和1079。根据前面给出的价量指标定义计算确定股指期货的价格收益率Rt、绝对收益率|Rt|、GK波动率σGK、成交量LnTVt、持仓量LnOIt、相对成交量LTV、相对持仓量LOI等，并进行价量指标的基本统计量描述如表1所示：

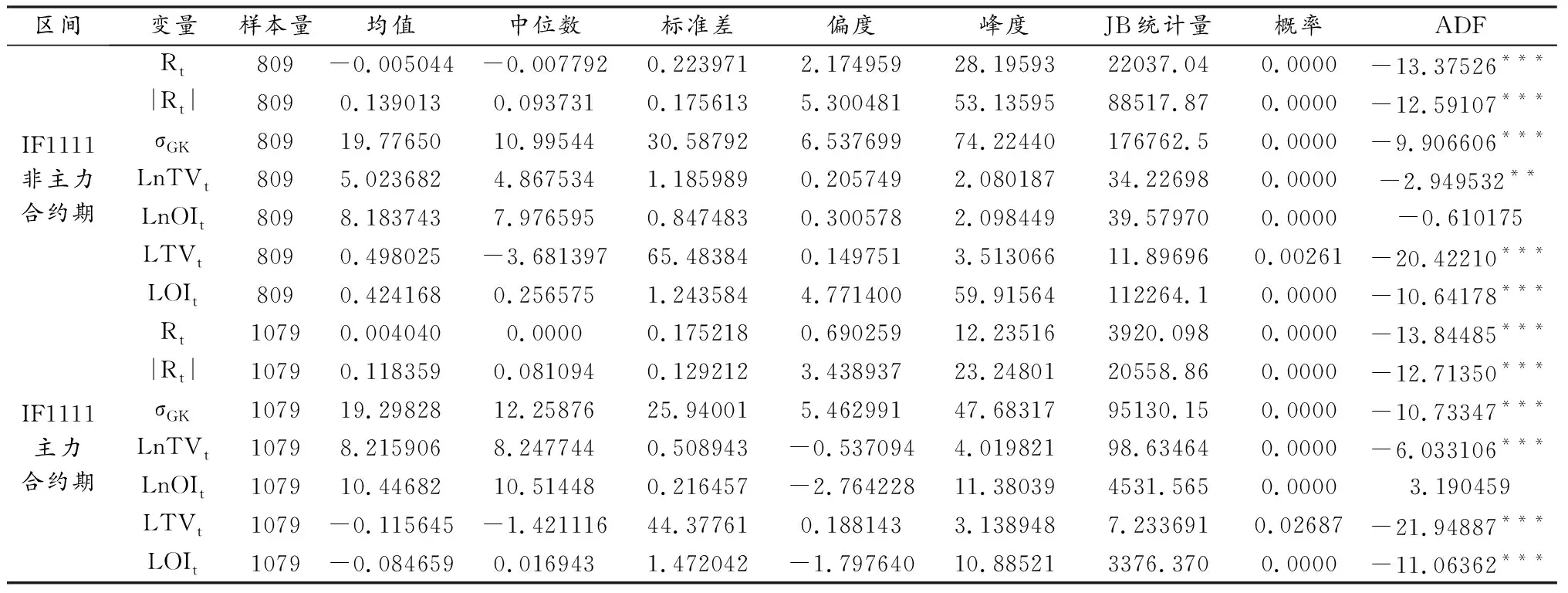
表1 股指期货合约IF1111价量数据的基本统计量

注：***表示1%的显著性水平下显著，**表示5%的显著性水平下显著，*表示10%的显著性水平下显著。

由表1可知，在股指期货合约IF1111的非主力合约期，所有数据的偏度都为正，说明所有数据有一个较长的右尾；价格收益率、绝对收益率、GK波动率、相对成交量、相对持仓量的峰度显著大于3，呈现明显的尖峰特征；JB统计量的值都很大，正态检验的结果说明数据的分布不服从正态分布；进行数据的ADF平稳性检验，除持仓量外，其他数据都是平稳数据。

在股指期货合约IF1111主力合约期，价格收益率、绝对收益率、GK波动率、相对成交量的偏度为正，有一个右尾；成交量、持仓量、相对持仓量的偏度为负，有一个左尾；所有数据的峰度都显著大于3，呈现明显的尖峰特征；除相对成交量外，所有的数据的JB统计量值都很大，不服从正态分布；进行数据的ADF平稳性检验，除持仓量外，其他数据都是平稳数据。

从总体上看，股指期货合约IF1111在非主力合约期和主力合约期的七类数据都不服从正态分布，具有尖峰后尾的特征，且除持仓量外都是平稳序列数据，这为后文的进一步分析提供了条件。

(二)股指期货合约的收益率与成交量、持仓量之间的关系

在分析股指期货合约的收益率与成交量、持仓量之间的关系时，需要进一步细分为价格收益率、绝对收益率与成交量、相对成交量、持仓量、相对持仓量之间的关系，具体采用Granger因果检验方法对各对关系进行检验，Granger因果检验结果如表2所示：

根据表2分析如下：

由协整性检验可知，在股指期货合约IF1111的非主力合约期和主力合约期的所有16对变量之间都存在程度不同的协整关系，协整关系的广泛存在为Granger因果检验提供了基础。

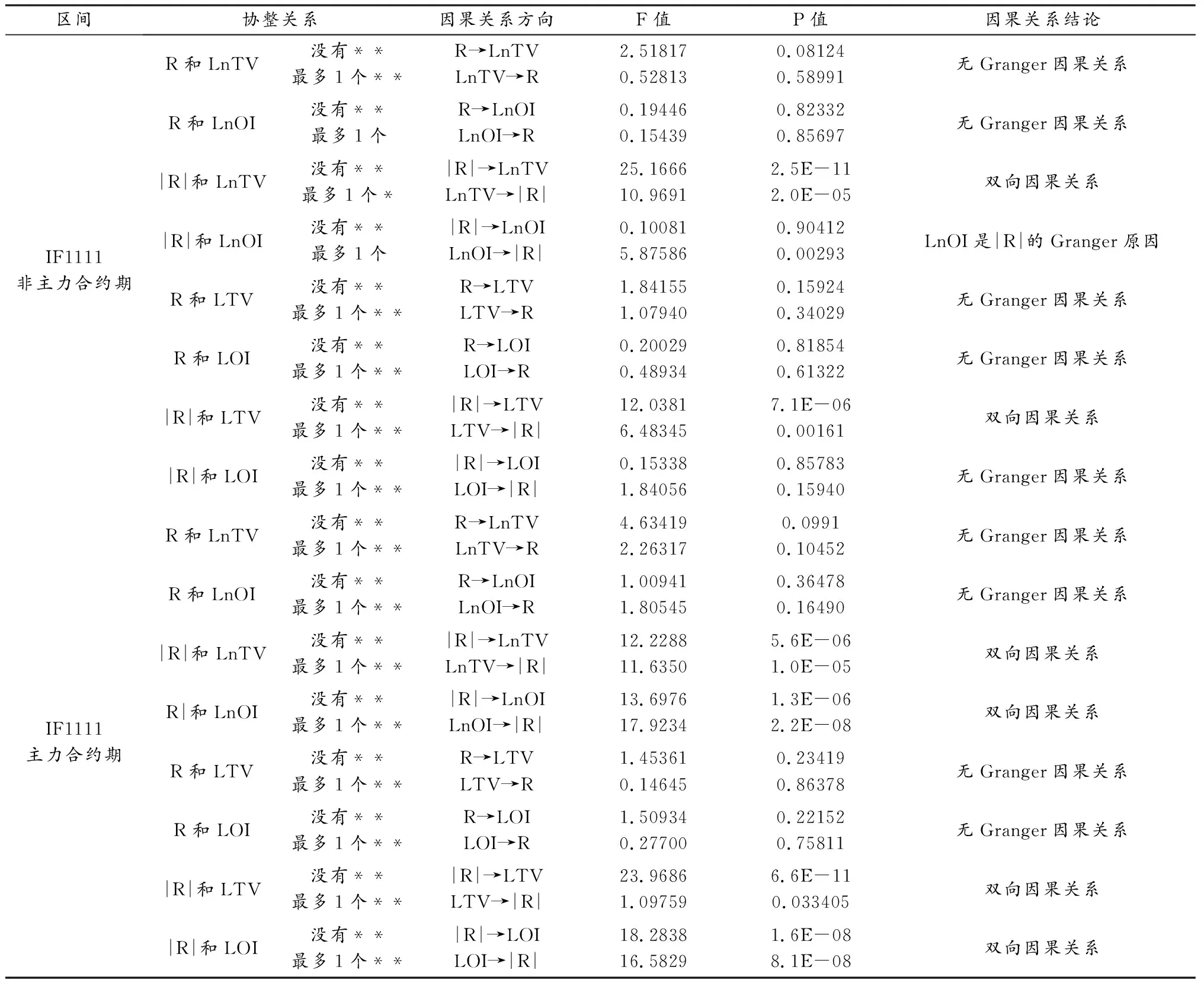
表2 股指期货合约IF1111的收益率与成交量、持仓量的Granger因果关系

注：**和*分别表示在5%和10%的显著性水平下拒绝不存在协整关系的原假设。

在股指期货合约IF1111的非主力合约期，价格收益率与成交量、持仓量均没有Granger因果关系，绝对收益率与成交量之间存在双向Granger因果关系，绝对收益率与持仓量之间存在单向的Granger因果关系，持仓量是绝对收益率的Granger原因。价格收益率与相对成交量、相对持仓量之间均没有Granger因果关系，绝对收益率与相对成交量之间存在双向Granger因果关系，绝对收益率与相对持仓量之间不存在Granger因果关系。

在股指期货合约IF1111的主力合约期，价格收益率与成交量、持仓量均没有Granger因果关系，绝对收益率与成交量之间存在双向Granger因果关系，绝对收益率与持仓量之间存在双向Granger因果关系。价格收益率与相对成交量、相对持仓量之间均没有Granger因果关系，绝对收益率与相对成交量之间存在双向Granger因果关系，绝对收益率与相对持仓量之间存在双向Granger因果关系。

可见，在股指期货合约IF1111的非主力合约期和主力合约期，收益率与成交量、持仓量之间的关系没有显著的差异，即表现为价格收益率与成交量、持仓量、相对成交量、相对持仓量之间都不存在Granger因果关系，而绝对收益率与成交量、持仓量、相对成交量、相对持仓量之间均存在一定程度的Granger因果关系。

(三)股指期货合约的波动率与成交量、持仓量之间的关系

表3 IF1111非主力合约期的波动率与成交量、持仓量关系

注：***表示1%的显著性水平下显著，**表示5%的显著性水平下显著，*表示10%的显著性水平下显著。

为了对模型2和模型3进行估计，需要首先得到预期、未预期的成交量和持仓量，采用ARIMA模型进行估计，根据AIC和SC准则，判断确定股指期货合约IF1111的非主力合约期的预期成交量和预期持仓量的估计模型分别为：ARIMA(2，1，2)和ARIMA(1，1，0)；判断确定股指期货合约IF1111的主力合约期的预期成交量和预期持仓量估计模型分别为：ARIMA(2，1，2)和ARIMA(2，1，0)。确定了预期成交量序列和预期持仓量序列后，用实际成交量序列减去预期成交量序列生成未预期成交量序列，用实际持仓量序列减去预期持仓量序列生成未预期持仓量序列。最后采用广义差分法对模型1、模型2、模型3进行估计，IF1111非主力合约期和主力合约期的波动率与成交量、持仓量之间关系的相关模型的估计结果表3、表4所示。

由表3，IF1111非主力合约期的波动率与成交量、持仓量的关系分析如下：

在模型1中，各变量的系数均较为显著，拟合优度也比较高。其中α1为25.23385，为正值，在0.01的水平上显著，说明成交量与五分钟内价格波动之间存在显著的正相关关系，即成交量作为反映市场信息数量的指标，成交量放大，表明到达市场的信息在增多，不同的信息导致价格变化在加剧，价格波动在增加。β1为-34.39071，为负值，在0.01的水平上显著，说明持仓量与五分钟内价格波动之间存在显著的负相关关系，即持仓量作为反映市场深度的指标，更多地反映套期活跃程度和未知情交易的情况，持仓量增加，说明市场深度在增加，套期交易和未知情交易增强，减缓了价格的波动。

在模型2中，将成交量和持仓量分解为预期成交量、未预期成交量、预期持仓量、未预期持仓量，对各个变量的系数分析如下，α1为131.1940，为正值，在0.01的水平上显著；α2为27.11704，为正值，在0.01的水平上显著，说明预期成交量和未预期成交量都与价格波动显著正相关，且预期成交量对价格波动的正向影响比未预期成交量对价格波动的正向影响更大。β1为-140.8775，为负值，在0.01的水平下显著；β2为-54.81422，为负值，在0.01的水平下显著；说明预期持仓量和未预期持仓量都与价格波动显著负相关，且预期持仓量对价格波动的负向影响比未预期持仓量对价格波动的负向影响更大。

在模型3中，再进一步把实际成交量分为大于预期成交量和小于预期成交量，把实际持仓量分为大于预期持仓量和小于预期持仓量等情况，分析成交量、持仓量对价格波动的影响。结果显示，无论实际成交量是高于预期成交量还是低于预期成交量，预期成交量和未预期成交量对价格波动的影响均为正，且在0.01的水平下显著，预期成交量和未预期成交量与波动率显著正相关，同时，α2<α1，α2+α3<α1，表明未预期成交量对价格波动的影响比预期成交量小。无论持仓量是高于预期持仓量还是低于预期持仓量，预期持仓量和未预期持仓量与波动率显著负相关，同时|β2|<|β1|，|β2+β3|<|β1|，表明未预期持仓量对价格波动的影响比预期持仓量小。α3>0，表明当成交量实际值大于预期值时，未预期成交量对价格波动的影响会加强，即正的成交量冲击对价格波动的影响比负的成交量冲击对价格波动的影响更大。β3<0，表明持仓量实际值大于预期值时，未预期持仓量对价格波动的影响会加强，即正的持仓量冲击对价格波动的影响比负的持仓量冲击对价格波动的影响更大。

表4 IF1111主力合约期的波动率与成交量、持仓量关系

注：***表示1%的显著性水平下显著，**表示5%的显著性水平下显著，*表示10%的显著性水平下显著。

由表4，IF1111主力合约期的波动率与成交量、持仓量的关系分析如下：

在模型1中，多数系数均较为显著，拟合优度也比较高。其中α1为39.48560，为正值，在0.01的水平上显著，说明成交量与五分钟内价格波动之间存在显著的正相关关系。β1为-41.37780，为负值，在0.01的水平上显著，说明持仓量与五分钟内价格波动之间存在显著的负相关关系。

在模型2中，将成交量和持仓量分解为预期成交量、未预期成交量、预期持仓量、未预期持仓量，对各个变量的系数分析如下：α1为47.56489，为正值，在0.05的水平上显著；α2为39.50581，为正值，在0.01的水平上显著，说明预期成交量和未预期成交量都与价格波动显著正相关，且预期成交量对价格波动的正向影响强于未预期成交量对价格波动的正向影响。β1为-52.56583，为负值，β2在0.05的水平上显著；为-41.79964，为负值，在0.01的水平下显著；说明预期持仓量和未预期持仓量都与价格波动显著负相关，且预期持仓量对价格波动的负向影响强于未预期持仓量对价格波动的负向影响。

在模型3中，再进一步把实际成交量分为大于预期成交量和小于预期成交量，把实际持仓量分为大于预期持仓量和小于预期持仓量等情况，分析成交量、持仓量对价格波动的影响。结果显示，无论实际成交量是高于预期成交量还是低于预期成交量，预期成交量和未预期成交量对价格波动的影响均为正，且在0.01的水平下显著，预期成交量和未预期成交量与波动率正相关；同时，α2<α1，α2+α3>α1，表明未预期成交量对价格波动的影响比预期成交量对价格波动的影响更大。无论实际持仓量是高于预期持仓量还是低于预期持仓量，预期持仓量和未预期持仓量与波动率负相关，同时|β2|>|β1|，|β2+β3|>|β1|，表明未预期持仓量对价格波动的影响比预期持仓量对价格波动的影响更大。α3>0，表明当成交量实际值大于预期值时，未预期成交量对价格波动的影响会加强，即正的成交量冲击对价格波动的影响比负的成交量冲击对价格波动的影响更大。β3<0，表明持仓量实际值大于预期值时，未预期持仓量对价格波动的影响会加强，即正的持仓量冲击对价格波动的影响比负的持仓量冲击对价格波动的影响更大。

四、结论与启示

将股指期货合约IF1111的存续期划分为非主力合约期和主力合约期，对股指期货的收益率、波动率等反映价格特征的变量与成交量、持仓量等反映数量特征的变量之间的动态关系进行实证分析，得到如下结论和启示：

第一，在股指期货合约的收益率与成交量、持仓量的关系分析中，股指期货的价格收益率与成交量、持仓量、相对成交量、相对持仓量之间不存在Granger因果关系，股指期货的绝对收益率与成交量、持仓量、相对成交量、相对持仓量之间存在某种程度的Granger因果关系。而且，这一结论在股指期货合约的非主力合约期和主力合约期没有显著的差异。

第二，在股指期货合约的波动率与成交量、持仓量的关系分析中，股指期货的非主力合约期和主力合约期的结论则存在显著的差异。在股指期货的非主力合约期，价格波动与成交量之间存在显著的正相关关系，预期的成交量对价格波动的正向影响比未预期的成交量大，正的成交量冲击对价格波动的影响比负的成交量冲击更大。价格波动与持仓量之间存在显著的负相关关系，预期的持仓量对价格波动的负向影响比未预期的持仓量大，正的持仓量冲击对价格波动的影响比负的持仓量冲击更大。

第三，在股指期货合约的波动率与成交量、持仓量的关系分析中，在股指期货的主力合约期，价格波动与成交量之间存在显著的正相关关系，未预期的成交量对价格波动的正向影响比预期的成交量大，正的成交量冲击对价格波动的影响比负的成交量冲击更大。价格波动与持仓量之间存在显著的负相关关系，未预期的持仓量对价格波动的负向影响比预期的持仓量大，正的持仓量冲击对价格波动的影响比负的持仓量冲击更大。

第四，股指期货投资者在分析价格收益率时，考察股指期货的成交量和持仓量没有太大意义，但在分析绝对收益率时，则可以密切股指成交量和持仓量这些变量。股指期货投资者在分析价格波动率时，需要区分是股指期货合约的非主力合约期还是主力合约期，还要知道成交量、持仓量与价格波动的方向是刚好相反的。这样，股指期货的交易者才能根据成交量、持仓量这些显性指标的变化，去比较准确地判断价格收益率和价格波动率这些隐性指标的变化，实施正确的交易策略，取得交易的最大成功。

参考文献：

[1]Karpoff J M..The Relationship between Price Changes and Trading Volume:A Survey[J].Journal of Financial and Quantitative Analysis,1987,(22):109-126.

[2]Cornell B.The Relation between Volume and Price Variability in Futures Markets[J].Journal of Futures Markets,1981,(01):302-316.

[3]Grammatikos T.,Sauders A.Futures Price Variability:A Test of Maturity and Volume Effect[J]. Journal of Business,1986,(59):319-330.

[4]Foster A J.Volume-Volatility Relation for Crude Oil Futures Markets[J].Journal of Futures Markets,1995,(15):929-951.

[5]Lamoureux,C.,and Lastrapes W.Heteroskedasticity in Stock Return Data:Volume versus GARCH Effect.[J].Journal of Finance,1990(45):221-229.

[6]Bessembinder H.,Seguin P J.Price Volatility ,Trading Volume,and Market Depth:Evidence from Futures Market[J].Journal of Financial and Quantitative Analysis,1993(28):21-39.

[7]Ragunathan, V. and Peker, A.Price Volatility, Trading Volume, and Market Depth: Evidence from the Australia Future Markets[J].Applied Financial Economics,1997,(07):447-454.

[8]Girma P B.,Mougoue M..An Empirical Examination of the Relation between Futures Spreads Volatility ,Volume,and Open Interest[J].Journal of Futures Markets,2002,(22):1083-1102.

[9]Terry A. Marsh, Niklas Wagner. Return-Volume Dependence and Extremes in International Equity Markets[R].Haas School of Business,UC Berkeley,2004,RPF-293.

[10]Mubarik, Javid. Relationship between Stock Return, Trading Volume and Volatility:Evidence from Pakistani Stock Market[J].Asia Pacific Journal of Finance and Banking Research,2009,3(3):1-17.

[11]McCarthy J,Najand M.,State Space Modeling of Price and Volume Dependence:Evidence from Currency Futures[J].Journal of Futures Markets,1993,(13):335-344.

[12]Nowbustsing, Naregadu.Returns, Trading Volume and the Volatility in the Stock Market of Mauritius[J].African Journal of Accounting,Economics,Finance and Banking Research.2009,5,(5):1-36.

[13]华仁海，仲伟俊.对上海期货交易所金属铜量价关系的实证分析[J].统计研究，2002,(08)：71-73.

[14]华仁海，仲伟俊.对我国期货市场价量关系的实证研究[J].数量经济技术经济研究，2002,(06)：119-121.

[15]华仁海，仲伟俊.我国期货市场期货价格收益、交易量、波动性关系的动态分析[J].统计研究，2003,(07)：25-30.

[16]周志明，唐元虎，施丽华.中国期市收益率波动与交易量和持仓量关系的实证研究[J].上海交通大学学报，2004,(03)：368-372.

[17]华仁海，仲伟俊.我国期货市场期货价格波动与成交量和空盘量动态关系的实证分析[J].数量经济技术经济研究，2004,(07)：123-132.

[18]田新民，沈小刚.基于交易量和持仓量的期货日内价格波动研究[J].经济与管理研究，2005,(07)：78-80.

[19]翟光磊.橡胶期货价格和交易量、持仓量的相关性分析[J].金融经济，2011,(18)：75-77.

[20]张孝岩，沈中华.股指期货推出对中国股票市场波动性的影响研究——基于沪深300股指期货高频数据的实证分析[J].投资研究，2011,(10)：112-122.