基于油水两相渗流的地层流体复合注水井试井模型

刘佳洁,孟英峰

李皋,魏纳 (油气藏地质及开发工程国家重点实验室 (西南石油大学),四川 成都 610500)

毕波 (中石油新疆油田分公司采油一厂,新疆 克拉玛依 834000)

李文政 (中石化胜利石油管理局石油开发中心,山东 东营 257000)

基于油水两相渗流的地层流体复合注水井试井模型

刘佳洁,孟英峰

李皋,魏纳 (油气藏地质及开发工程国家重点实验室 (西南石油大学),四川 成都 610500)

毕波 (中石油新疆油田分公司采油一厂,新疆 克拉玛依 834000)

李文政 (中石化胜利石油管理局石油开发中心,山东 东营 257000)

目前,注水井试井以单相渗流为基础,缺乏考虑含水率、水驱前缘半径等参数,以及缺乏分析地层性质与流体性质的变化对压力特征曲线影响。根据质量守恒原理,结合注水井岩心归一化相渗曲线,建立含水饱和度与相对渗透率关系,以油水两相流渗流理论为基础,建立地层流体复合注水井试井模型,通过Laplace变换,利用Stehfest数值反演得实空间解,绘制了压力和压力导数双对数样板曲线,分析水驱前缘半径、油水两相驱前半径缘、两相区含水率、两相区含水饱和度等注水油藏重要参数对试井曲线的影响,讨论流体性质与地层性质的变化对试井曲线的影响。研究结果对认识注水油藏的物性参数及注水情况起到重要作用,为注水油藏进一步合理注水开发提供依据。

油水两相渗流;试井分析;水驱前缘半径;含水率;含水饱和度

注水井试井长期以来采用油井压力降落试井分析方法[1～3]。文献 [4～6]基于单相流渗流理论研究注水井的压力动态特征变化,文献 [7,8]研究了相渗曲线以及相渗曲线对注水井油水两相流试井曲线的影响,文献 [9]将含水饱和度与相对渗透率关系引入试井模型。目前,国内外注水井试井研究主要以单相流渗流理论为基础,用于分析渗透率等注水地层基本物性参数。然而水驱前缘、含水饱和度、含水率等参数的影响缺乏研究,流体性质与地层性质对压力特征曲线影响的不同缺乏分析。笔者运用经归一化处理的相渗曲线建立含水饱和度与相对渗透率关系,根据质量守恒原理建立基于油水两相渗流的地层流体复合注水井试井模型 (一区地层性质相同,流体性质不同分为水区和油水两相区;二区与一区地层性质不同,流体为油水两相区),分析了流体性质与地层性质对压力特征曲线的影响。该模型用于分析注水井储层基本物性参数,同时可用于分析注水油藏含水率、含水饱和度、水驱前缘位置等参数,全面分析注水地层物性参数和注水情况,为注水油藏进一步合理注水开发提供依据。

1 相对渗透率与含水饱和度关系的建立

对一个具体的油藏,由于取心分析的岩样具有不同的渗透率和孔隙度,所得的相渗曲线也不相同,为了消除不同曲线对束缚水饱和度与残余油饱和度的影响,需选择一些有代表性的相渗曲线进行归一化处理。油水归一化相对渗透率定义及表达式为[10]:

油水相对渗透率比值与含水饱和度之间满足指数式关系[10]:

根据岩心试验,由平均每一块岩心的c、d值得到油气藏标准化相渗透率,然后反求油气藏的相对渗透率曲线。根据多块岩心归一化处理后的结果数据,得到a和b值,从而建立含水饱和度与相对渗透率关系。

2 物理模型

所建立的物理模型如图1所示。模型假设如下:①圆形等厚油藏中心一口注水井,定量均匀注水;②注入流体径向流入地层,渗流为等温达西渗流;③油、水和岩石微可压缩,其压缩系数、流体黏度均为常数;④考虑井筒储集效应和表皮效应的影响;⑤外边界条件可以是无穷大地层、圆形封闭或圆形定压;⑥一区、二区地层性质不同;⑦地层一区包含水相区和油水两相区,二区为油水两相。

3 数学模型

3.1 无量纲量定义

图1 物理模型

3.2 数学模型

3.3 数学模型求解

4 典型试井曲线分析

利用Stehfest[13]数值算法进行数值反演,得到定注入量实空间无量纲井底压力动态解pD,从而编程绘制出基于油水两相渗流的地层流体复合注水井试井模型关于pD～tD/CD与p'DtD/CD～tD/CD的无量纲试井曲线。

图2是一区为水相和油水两相、二区为油水两相的地层流体复合注水井试井模型在圆形封闭、圆形定压、无穷大外边界条件下的试井曲线。图2中,第Ⅲ段压力导数出现水平段,这是地层中一区水相系统产生径向流;第Ⅳ段是一区油水两相系统影响段;第Ⅴ段是二区油水两相系统影响段;第Ⅵ段是外边界条件影响段。

图3为井筒储集系数、表皮因数一定时不同含水率fw下一区为水相和油水两相、二区为油水两相无穷大外边界条件下的试井曲线。如图3所示,含水率变化越大,水相系统与油水两相系统流体性质差异越大,一区油水两相系统影响段 (第Ⅳ段)和二区油水两相系统影响段 (第Ⅴ段)的压力和压力导数曲线下掉得越大。图4为不同含水饱和度Sw情况下一区为水相和油水两相、二区为油水两相无穷大外边界条件下的试井曲线,两区流体性质差异越大,试井曲线变化越明显。对比图3和图4,可以看出流体性质与地层性质的变化对注水井试井曲线影响不同,因此对于不同地层性质注水油藏需同时考虑两因素的影响,否则不能正确反映地层真实情况。

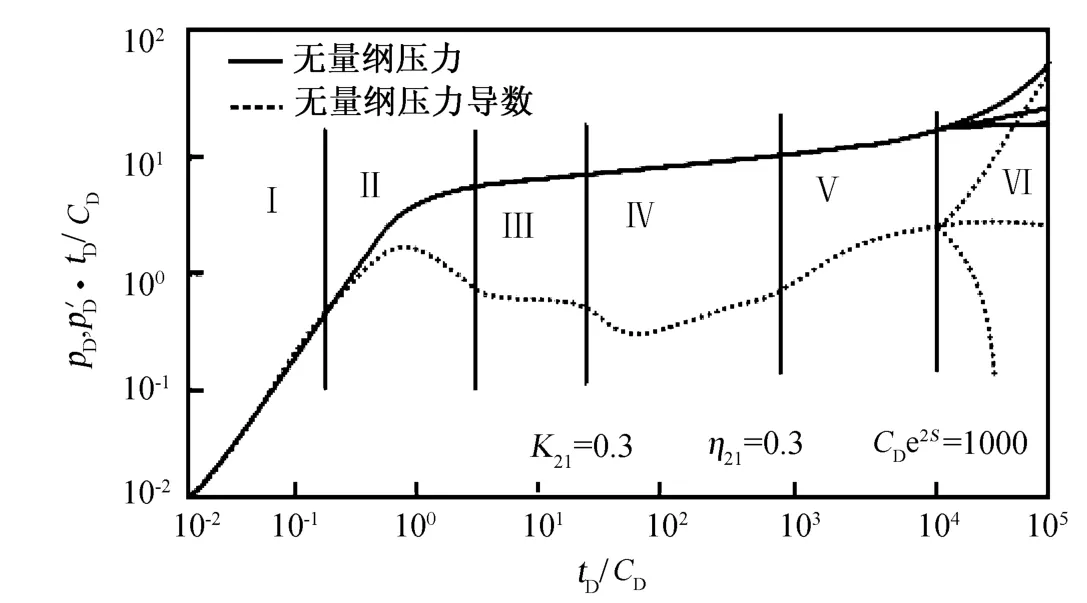
图2 一区为水相和油水两相、二区为油水两相的试井曲线

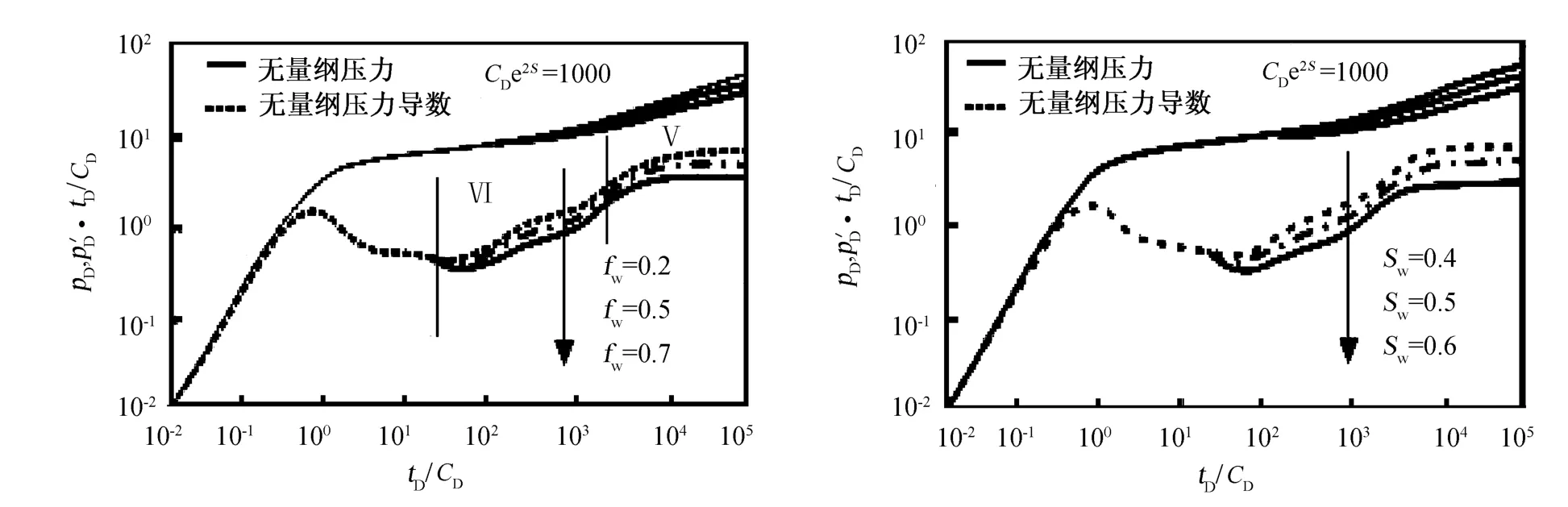
图3 不同含水率fw情况下的试井曲线 图4 不同含水饱和度Sw情况下的试井曲线

图5为井筒储集系数、表皮因数一定时不同渗透率比值RK21下一区为水相和油水两相、二区为油水两相的无穷大外边界条件下的试井曲线,二区与一区渗透率比值RK21越小,一区与二区之间的地层性质差异越大,二区 (第Ⅴ段)压力和压力导数曲线上翘得越大。图6为井筒储集系数、表皮因数一定时,不同水驱前缘半径Rw下一区为水相和油水两相、二区为油水两相的无穷大外边界条件下的试井曲线,水驱前缘半径越远,试井曲线凹点越往后移。

5 结论

1)基于油水两相流渗流理论,结合经归一化处理的含水饱和度与相对渗透率关系,考虑地层流体双重复合,建立一区为水相和油水两相、二区为水相的地层流体复合注水井试井模型,利用拉普拉斯变换和Stehfest数值反演方法,绘制该模型试井典型曲线。

图5 不同渗透率比值RK21情况下的试井曲线 图6 不同水驱前缘半径Rw情况下的试井曲线

2)该模型可分析注水油藏纯水驱前缘位置、油水两相驱前缘半径、含水饱和度、含水率、渗透率等重要参数,并且地层性质与流体性质对试井曲线的影响不同,对于不同地层性质的注水油藏,需同时考虑地层性质和流体性质的影响。

[1]Puntel E A,Oliveira de,Serra K V.Oil/water relative permeability estimation from fall Off tests[J].SPE26984,1994.

[2]Thomson L G,Reynolds A C.Well testing for heterogeneous reservoirs under single and multiphase flow condition[J].SPE30577, 1995.

[3]Roadifer R D.Pressure behavior of wells completed in multiphase reservoir containing a constant pressure boundary[J].SPE36555, 1997.

[4]尹洪军,付春权,万贵春,等.多重复合低渗透油藏注水井压力动态分析[J].石油学报,2002,23(4):70～74.

[5]王国辉,尚建林,郭建国,等.用试井方法分析百口泉组油藏储集层物性变化[J].新疆石油地质,2007,28(5):641～643.

[6]许明静,程时清,杨天龙,等.油水两相流不稳定试井压力分析[J].石油钻采工艺,2009,31(4):71～74.

[7]张人雄,毛中源,李建民,等.新疆宝浪油田相对渗透率曲线研究[J].新疆石油地质,2000,21(2):138～140.

[8]向祖平,张烈辉,陈辉,等.相渗曲线对油水两相流数值试井曲线的影响[J].西南石油大学学报,2007,29(4):74～78.

[9]刘佳洁,孟英峰,李皋,等.三区流体复合注水井试井模型研究[J].石油天然气学报(江汉石油学院学报),2013,35(2):120～125.

[10]李传亮.油藏工程原理[M].北京:石油工业出版社,2005.

[11]贾永禄,聂仁仕,王永恒,等.二次梯度非线性渗流问题求解[J].石油天然气学报(江汉石油学院学报),2008,30(4):119～122.

[12]刘永良,刘彬,刘大伟,等.三重介质气藏单井生产动态分析模型研究[J].石油天然气学报(江汉石油学院学报),2011,33 (2):123～127.

[13]贾永禄,赵必荣.拉普拉斯变换及数值反演在试井分析中的应用[J].天然气工业,1992,12(1):60～64.

[编辑]黄鹂

TE353.3

A

1000-9752(2014)02-0128-05

2013-07-21

国家自然科学基金青年基金项目(51104124,51204140);国家科技重大专项(2011ZX05021-003)。

刘佳洁(1985-),男,2010年西南石油大学毕业,博士生,现从事试井分析、欠平衡钻井方面的研究工作。