改进的郭涛算法在剩余静校正中的应用

曹中林,周强,吕文彪

张华,陈爱萍 (中国石油集团川庆钻探工程有限公司地球物理勘探公司,四川 成都 610213)

改进的郭涛算法在剩余静校正中的应用

曹中林,周强,吕文彪

张华,陈爱萍 (中国石油集团川庆钻探工程有限公司地球物理勘探公司,四川 成都 610213)

在低信噪比地震资料处理中,剩余静校正是其中的关键处理环节。传统的剩余静校正方法容易陷入局部极值,难以实现全局寻优,从而造成叠加剖面成像效果不佳。为此,提出了一种高精度的非线性剩余静校正方法,该方法以互相关值最大为目标函数,采用了逐步缩小范围的郭涛算法进行剩余静校正量的全局寻优。通过理论模型和低信噪比资料的测试表明,该方法优于传统的剩余静校正方法,能够快速逼近全局最优解,并且能够有效改善低信噪比地震资料的成像效果。

改进的郭涛算法;反演;剩余静校正

我国西部山地地区,地形起伏多变,地表结构复杂,山体部分老地层出露地表,导致采集的地震数据静校正问题特别严重,很大程度上影响了地震数据的最终成像效果。地震资料在做了野外静校正之后,有效反射波的同相轴应该呈双曲线分布,但实际上由于静校正计算中难免存在误差,使地震记录中还残留一定的时差,有效反射波的同相轴就不是理想的双曲线,随后的叠加成像效果也就不理想。因此,有必要将剩余时差在速度分析和叠加之前予以去除,这就是剩余静校正的主要任务。

目前,常规的剩余静校正方法有:共地面点法、Satan算法和最大能量法[1～2],都不能较好地解决低信噪比地震资料的剩余静校正问题。因此大量的学者引入了非线性反演方法进行剩余静校正量的求取,例如遗传算法[3～5],模拟退火方法[6～9]以及蒙特卡罗方法[10～11],这些非线性反演方法在一定程度上改善了地震资料的最终成像效果,但是都存在反演效率较慢以及容易陷入局部极值的问题。而郭涛算法[12]是一种基于子空间搜索 (多父体杂交)的群体随机搜索算法,可以用来求解复杂函数优化问题。笔者结合了郭涛算法的特性,提出了逐步缩小搜索范围的改进策略,并将其应用到剩余静校正量的求取中,实现了剩余静校正量的全局寻优。理论模型和实际地震数据的测试表明,该方法优于传统的剩余静校正方法,针对低信噪比地震资料处理具有一定的效果。

1 郭涛算法特点及程序

郭涛算法是一种精确的全局寻优算法[13～17],该算法有以下3个特点:

1)采用了演化计算中群体搜索策略,可以实现全局寻优,适合于复杂的非线性函数优化的问题。

2)进行了多父体的线性重组,特别是子空间中随机搜索的非凸性,保证了随机空间中随机搜索的遍历性。从N个父体向量P={X1,X2,…,XN}中随机选择M个个体组成向量X'={X1',X2',…,XM'},构成子空间V={X︱a·X'}作为其搜索空间,其中a={a1,a2,…,aM}是M维向量,满足条件:

3)采用了“劣汰策略”,每次只把群体中适应性最差(目标函数值最大)的个体淘汰出局,淘汰压力最小,既保证了群体的多样性,也保证了适应性最好(目标函数值最小)的个体可以“万寿无疆”。这种“群体爬山策略”,保证了整个群体最后集体登上最高峰(深谷)。

郭涛算法的具体程序如下:

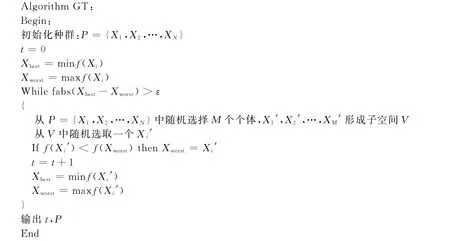
其中:P是种群;X1,X2,…,XN是种群P中的N个个体;t为迭代次数;Xbest为根据目标函数求取的种群中最小适应值;Xworst根据目标函数求取种群中最大适应值;f为适应度函数;ε是用户给定的误差精度,当大于给定精度则进行循环迭代,如果小于精度就终止并输出最终的结果。

2 改进的郭涛算法

为了加快郭涛算法的收敛速度,笔者提出了逐步缩小搜索范围的策略。由于郭涛算法在很少的搜索次数之后,种群就能够迅速聚集到一定的范围之内。为此,笔者提出改进方案:在进行一定次数的搜索之后,就统计种群中个体的最大值及最小值,根据这个最小值与最大值,可以定义一个新的搜索区间,下次再搜索的时候,就在这个新的区间范围内进行搜索。通过该方案可以逐步缩小搜索范围,进一步提高郭涛算法的收敛速度。

在计算剩余静校正的方法中,常用的一种方法就是最大能量方法,该方法是指在应用正确的静校正量之后可使地震剖面的叠加能量达到最大。目前计算非线性剩余静校正的方法都是以最大能量法为基础。最大能量法的目标函数为:

式中:S、R分别是炮点和检波点的剩余静校正量;E(S,R)为对应的叠加剖面的能量;Ajk是第j个共中心点道集中的第k道;p为地震数据的共中心点道集数;Q为每一个道集的道数;t是地震数据的时间点;t1和t2为剩余静校正中地震数据的计算时窗。

同一个炮点或检波点都有多道,而该炮点(或检波点)剩余静校正量只会影响到与该炮点(或检波点)有关的CMP(共中心点)道集的叠加能量。由此CMP道集的叠加能量E可写为:式中:τ是自相关的时移量;C(t)为CMP道集;K(t)是该CMP道集的叠加;d为常数。

由此,估计叠加能量的最大值也就等效于估计它的互相关的最大值。有了这个目标函数以后,就可以采用上面所述的改进郭涛算法进行非线性迭代搜索。具体步骤如下:

1)在给定静校正量范围内,初始化种群P={X1,X2,…,XN},t=0(第1次迭代)。

2)根据目标函数E(能量最大)评估种群,找出最好个体与最差个体。

3)保存最优解。

4)当不满足给定误差值的时候,重复执行下面的步骤5)～9)。

5)t=t+1。

6)从种群中选出M个个体{X1',X2',…,XM'},形成子空间V。7)按照下面的公式进行多父体重组策略生成新的个体:

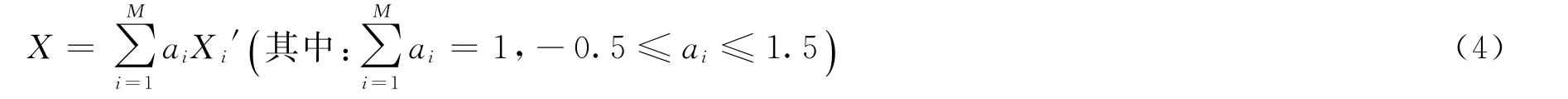
8)如果该新的个体比当前种群最差个体要好,则替代最差个体。

9)当进行了几次迭代之后,找出当前种群中所有个体的最大值与最小值,由此确定新的静校正量搜索空间,重新回到步骤2)。

通过以上改进的郭涛算法进行迭代搜索,最终找到剩余静校正量的最优解,从而完成剩余静校正量的求取。

3 资料测试效果

3.1 理论模型测试

为了验证该方法的正确性,采用理论模型进行了测试。图1(a)是在共中心点道集地的震数据上加入了随机静校正量,然后再叠加产生的数据,从图中可以看出,静校正前叠加剖面的同相轴连续性极差;图1(b)是用改进的郭涛算法进行剩余静校正后的叠加数据,叠加剖面的同相轴有了较好的连续性。通过理论模型的测试,验证了基于改进的郭涛算法的剩余静校正方法的正确性。

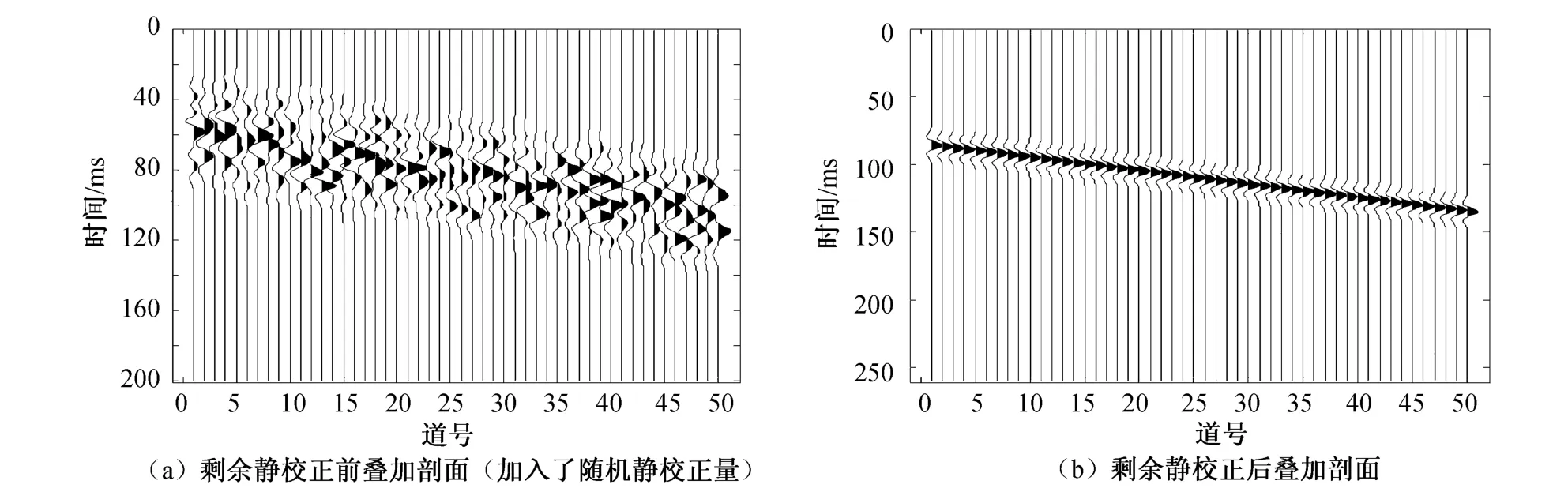
图1 理论模型应用效果

3.2 实际资料应用效果

为了验证该方法的实际应用效果,笔者选取了四川某地区实际地震数据进行应用。数据大小为1.7G,采样率为2ms-1,采样时间为5000ms,有效反射目的层为3000ms左右,沿着目的层上下开时窗600ms。图2(a)是剩余静校正前的叠加结果,叠加剖面的成像效果不好;图2(b)是最大能量法剩余静校正后的叠加结果,剖面靠右端的地方可以看到一些连续的同相轴,但是成像效果还是不佳;图2(c)是基于改进的郭涛算法的剩余静校正后的叠加结果,剖面的同相轴连续性更好,信噪比更高,构造更加清晰,成像效果改善明显。通过实际数据的应用,以及与传统最大能量法的效果对比可知,笔者提出的基于改进的郭涛算法的剩余静校正方法明显优于传统的剩余静校正方法,能够有效改善低信噪比地震资料的成像效果。

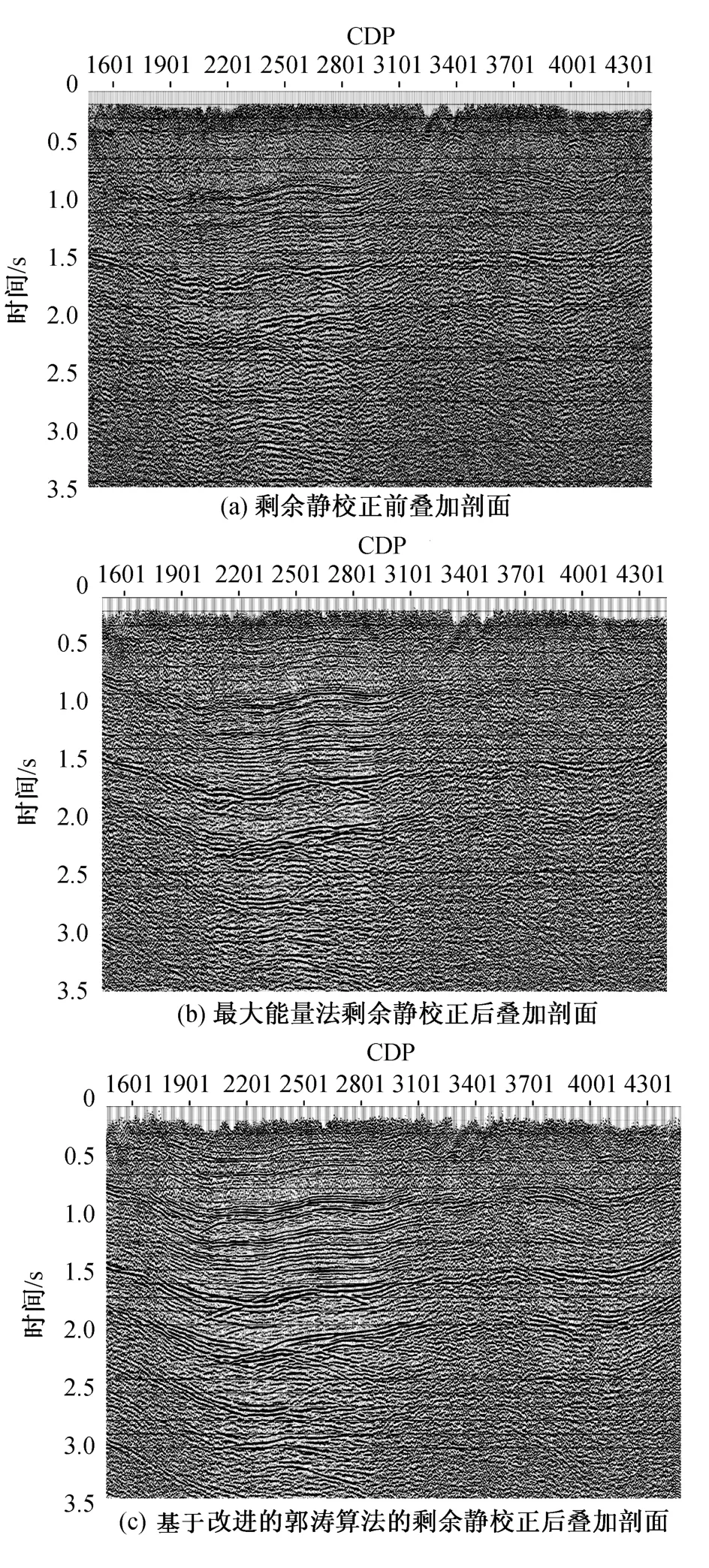
图2 实际数据应用效果

4 结论与认识

1)基于改进的郭涛算法的剩余静校正方法充分利用了郭涛算法的基于子空间搜索 (多父体重组)和群体爬山法相结合的特性,保证了搜索空间的全局性,同时采用了逐步缩小搜索范围的策略,使得该算法的搜索效率更高。

2)理论模型反演试算和实际资料处理结果表明,基于改进的郭涛算法的剩余静校正方法具有很高的精度,效果优于常规的剩余静校正方法,能够适应低信噪比地震资料的处理,具有较好的推广应用前景。

[1]程金星,董敏煜,秦顺亭,等.三种算法联合迭代反演求取最佳剩余静校正量[J].地球物理学报,1996,39(3):416～422.

[2]吴波,徐天吉,唐建明,等.三种反射剩余静校正方法对比研究与应用[J].石油物探,2012,52(2):172～177.

[3]李丽,陈秀娟,井西利.多尺度地震剩余静校正方法及应用[J].新疆石油地质,2011,32(4):402～405.

[4]Wilson W G,Laidlaw W G,Vasudevan K.Residul statics estimation using the genetical algorithm[J].Geophysics,1994, 59(5):766～774.

[5]何超群,王彦春,张品.利用遗传-粒子群优化混合算法求取剩余静校正量[J].新疆石油地质,2011,32(6):656～659.

[6]林依华,张中杰,尹成,等.复杂地形条件下静校正的综合寻优[J].地球物理学报,2003,46(1):101～106.

[7]李丽,陈秀娟,井西利.基于均匀设计的自动剩余静校正方法[J].新疆石油地质,2009,30(1):121～123.

[8]张红梅,吕小林,刘洪.改进的约束单纯形-模拟退火剩余静校正[J].地球物理学进展,2004,19(2):341～347.

[9]何超群,王卿,张品,等.退火遗传算法在剩余静校正中的应用[J].物探与化探,2011,35(6):789～792.

[10]陈枫,王彦春,王海泉,等.利用蒙特卡罗方法的剩余静校正及其应用[J].物探与化探,2012,36(4):628～631.

[11]潘树林,吴波,高磊,等.自然血亲排斥策略对遗传算法的改进及其在剩余静校正中的应用[J].石油地球物理勘探,2010,45 (6):802～806.

[12]郭涛.演化计算与优化[D].武汉:武汉大学软件工程国家重点实验室,1999.

[13]Guo Tao,Kang Li-shan.A new evolutionary algorithm for function optimization[J].Wuhan University Journal of Nature Sciences, 1999,4(4):409～414.

[14]郭涛,康立山,李艳.一种求解不等式约束下函数优化问题的新算法[J].武汉大学学报(自然科学版),1999,45(5):771～775.

[15]杨国荣,杨承中.郭涛算法在模板匹配中的应用[J].软件导刊,2011,10(12):45～46.

[16]郭艳,康立山,刘福江.基于郭涛算法的演化神经网络[J].计算机工程与应用,2007,43(20):45～46.

[17]曹中林,昌彦君,何展翔.基于演化算法的复电阻率频谱参数反演[J].工程地球物理学报,2005,2(1):33～37.

[编辑]龚丹

P631.44

A

1000-9752(2014)02-0062-04

2013-06-04

中国石油天然气集团公司科学研究与技术开发项目 (2011B-3706)。

曹中林(1981-),男,2004年大学毕业,硕士,工程师,现主要从事地震资料处理方面的方法研究与软件开发工作。