基于GM-BP建模的城市工业废气排放量预测
张雪伍,蒋家超
(1.常熟理工学院 计算机科学与工程学院,江苏 常熟 215500;2.中国矿业大学 环境与测绘学院,江苏 徐州 221116)
1 引言
工业废气指企业厂区内燃料燃烧和生产工艺过程中产生的各种排入空气的含有污染物的气体总量[1].随着工业化水平的提高,分布于城市周围的工矿企业的数量和生产规模不断增大,废气排放量也呈现逐年上升的发展态势.废气完全降解需要一定的时间周期,因此环境中的废气总量具有一定的累积效应,在总量上呈现出复杂的非线性增长,对城市的空气质量构成了巨大的威胁.有效地对城市工业废气排放量进行预测,可以更好地控制和改善城市大气质量,为城市工业合理发展和科学布局提供依据,因此设计准确、高效的城市工业废气排放量预测模型成为城市工业发展和规划研究领域中的热点.
为了对城市工业废气排放量进行准确预测,国内外学者对其进行了大量的研究,提出了许多预测方法,主要有回归分析法、时间序列法、ARMA模型等,近年来又引入神经网络、灰色系统等理论探讨新的预测方法[2-5].传统的回归分析法、时间序列法、ARMA模型等是趋势预测,假定城市工业废气排放量是线性变化的,然而实际上城市工业废气排放量受到国家产业政策、国际贸易环境等因素的影响,呈现出非常复杂的非线性,同时具有趋势性、随机性和突变性,用传统线性模型对其进行预测精度较低[2-3].城市工业废气排放量变化过程是同时含有已知信息和未知信息的动态系统,因此很多学者将其看作一个灰色系统,构建基于GM(1,1)的城市工业废气排放量预测模型,取得了较好的预测效果.然而灰色模型仅仅适应于变量呈指数级增长的数据预测[6-8],现实中,城市工业废气排放量呈现趋势性变化的同时,还伴随着随机性和非线性,单一GM(1,1)模型对波动性较大的城市工业废气排放量的预测精度较低.BP神经网络模型能够对非线性关系进行无限逼近,适合对非线性、波动性较大的问题进行建模,且预测精度较好[9-10],但由于没有考虑变化的趋势性,预测的稳定性不高,经常出现较大误差.因此,本文将GM(1,1)模型与BP神经网络模型相结合构建组合预测模型,实现优势互补,提高城市工业废气排放量的预测精度.将GM(1,1)(简称,GM)与BP进行结合,构建GM-BP交叉组合模型对城市工业废气排放量进行预测.先通过GM(1,1)对城市工业废气排放量变化趋势进行预测,然后利用BP神经网络对GM(1,1)模型的趋势预测值进行随机误差修正,以适应城市工业废气排放量的随机性和复杂非线性,提高预测精度.最后,通过对南京市工业废气排放量进行仿真,对提出的GM-BP模型进行了检验.
2 城市工业废气排放量预测原理
城市工业废气排放量在一定程度上反映了该城市的工业化水平,受到诸多因素影响,如工业生产工艺水平、城市工业发展规模等,并且各种因素之间存在高度的非线性相关.它的变化是非线性的,这种非线性是由变化的趋势性和随机性叠加而形成的.城市工业废气排放量预测是根据城市工业废气排放量的历史数据和相关影响因素的历史数据,基于一个预测模型对其未来的排放量进行预测,表示如下:

式中y是年度城市工业废气排放量,g是年度城市工业废气排放量趋势值,ε是城市工业废气排放量的随机误差,由相关影响因素预测.
3 GM(1,1)与BP神经网络
3.1 GM(1,1)模型
灰色预测通过对原始数据处理和灰色建模,发现系统的演化规律,进而对系统未来的发展状态做出科学的定量预测[6-9].灰色预测模型的构建是以对系统发展进程进行充分的定性分析为依据的,同时模型还要经过多种检验合格后方能用来预测.GM(1,1)模型是灰色系统中常用的数列预测模型[7].在对原始数列进行定性分析的基础上,确定适当的序列算子,然后对算子计算后的数列构建GM(1,1)模型,达到指定的精度便可以对数列的未来变化进行预测[10].
3.2 BP神经网络
BP神经网络是一种基于信号正向传播和误差逆向传播的多层前馈神经网络,在大量的学习样本和足够的训练次数下,能够记忆输入与输出之间的映射关系[11].它一般由输入层、隐含层(为一层或多层)和输出构成,相邻各层之间的神经元为全连接,层内神经元之间无连接.训练过程中输入样本从输入层经由隐含层逐层处理后,传向输出层,若实际输出与期望输出误差不能满足要求,则进入误差的反向传播过程,输出误差被分摊到各层的所有神经单元,但其不能被反馈到最前层.
BP神经网络学习过程中,通过正向逐层计算各层神经元的输出和反向对连接权重和阈值进行调整两个过程的多次反复交替进行,直至达到收敛为止,或达到训练次数的上限,学习过程结束,便可用该模型进行预测.理论上,BP网络可以在任意精度下对映射关系进行建模,但由于受到训练次数、学习样本数量、隐含层神经元个数等因素的影响,对于小样本时序数据的预测存在一定的误差.
4 GM-BP的城市工业废气排放量预测
城市工业废气排放量的变化在总体上呈现出一定的趋势性,在细节上又表现出复杂的非线性波动.这种波动是由与工业废气排放直接或间接相关的影响因素变化而引起的.故此,引入交叉组合灰色神经网络模型对工业废气排放量进行预测,模型结构如图1所示.
X=(x1,x2,…xi)T为 BP 网络的输入向量;H=(h1,h2,h3…hj)T为隐含层的输入向量;ε=(ε1,…εm)T为 BP 网络的输出残差向量;Y=(y1…ym)(ym为第m个预测指标的时间序列数据行向量)是MG(MG1…MGm)模型的输入行向量;G=(g1,…gm)T为 GM-BP模型的输入向量的灰色预测部分向量;ε=(ε1,…,εm)T向量为 GM-BP模型的残差预测部分;O=(o1,…,om)T为GM-BP模型的输出向量. 模型的期望输出为D向量,D=(d1,d2,…dm)T.
(4)健全电网数据管理机制,强化数据安全管理工作。在大数据时代下,数据是一种重要的资源,为此,电力行业必须强化对数据的安全管理,建立健全的数据安全管理机制,以防重要数据丢失,加强数据的安全性与保密性,有效保护数据价值。
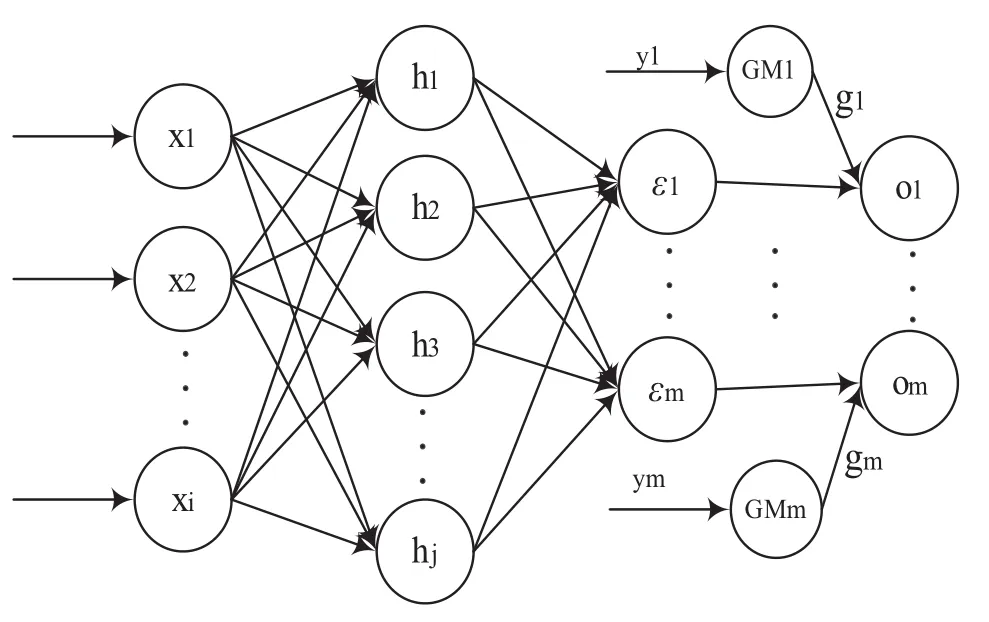
图1 GM-BP预测模型结构
4.1 GM(1,1)的趋势预测
Ym为GMm模型的输入的原始数据序列,有e个数据,记为:
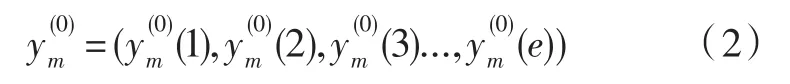
对y(0)m作1-AGO算子运算,得式(3):
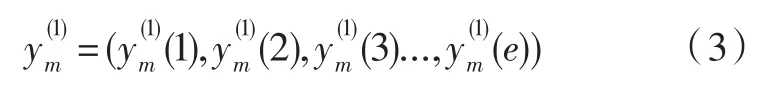
用均值紧邻算子作用于y(1)m得式(4):

根据GM(1,1)模型,可得:
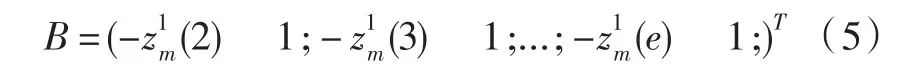

通过a^=[a,b]T=(BTB)-1BTP来构建时间相应函数为

根据式(3)求得 y(1)m的模拟值

通过1-AGO算子的逆向操作获得y(0)m的模拟值

由式(1)与式(9)可以计算GM(1,1)的模拟误差为
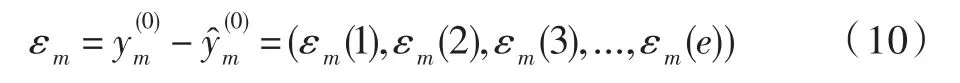
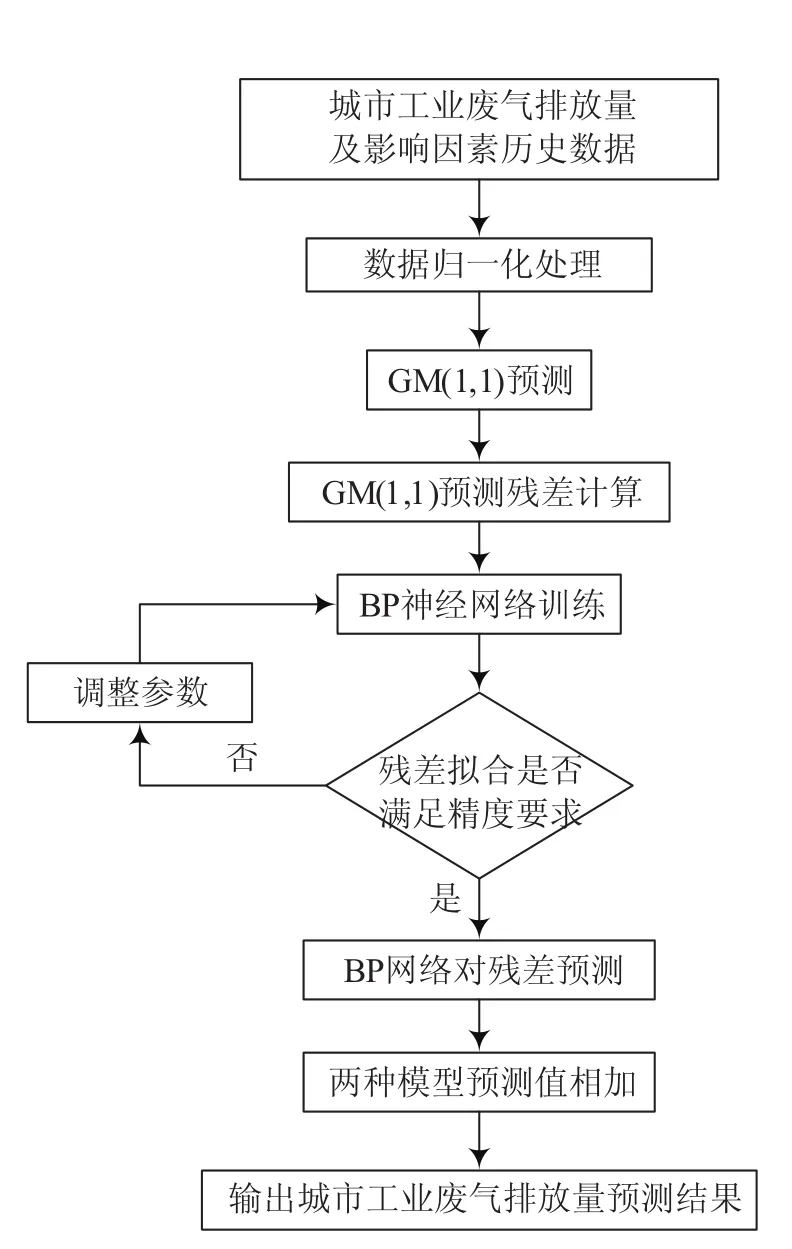
图2 城市工业废气排放量GM-BP模型预测流程
4.2 BP网络的GM(1,1)预测值残差修正
预测时,将GMm(1,1)模型的输出向量与BP模型的误差预测值 ε^m相加,作为GM-BP模型的对第m预测指标的最终预测值.

最终GM-BP模型的预测结果为

基于GM-BP模型的城市工业废气排放量预测流程如图2所示.
5 仿真实验
5.1 城市工业废气排放量及相关数据来源
城市工业废气排放量的相关因素众多.综合考虑数据本身的准确性和可获得性,选取了城市工业废渣(x1(亿吨))、城市工业废水(x2(亿吨))和城市工业总产值(x3(亿元))作为直接影响因素,城市总人口(x4(万人))和城市GDP(x5(亿元))作为间接影响因素参与城市工业废气排放量(y(亿立方米))的预测.实验数据来自于1981~2011年南京市统计年鉴(见表1),选取1981~2006年的数据作为训练数据,2007~2010年数据用来对模型进行检验.

表1 1981~2010年南京市工业废气相关因素
5.2 GM(1,1)仿真
在Matlab7.0平台上编写GM(1,1)计算程序,将1981~2006年南京城市工业废气排放量作为输入变量,进行GM(1,1)建模,获得的时间响应式如式(13)所示.

利用式(13)对2007~2010年南京市工业废气排放量进行预测,预测结果见图3.
由图3可知,GM(1,1)模型能较好反映南京城市工业废气排放量的变化趋势,但在废气排放量的波动预测方面,精度较低.
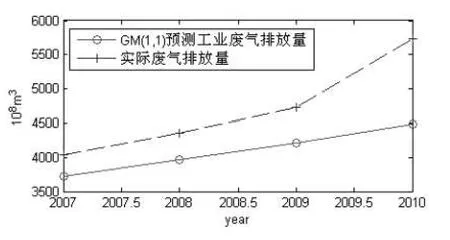
图3 GM(1,1)预测结果
5.3 GM(1,1)残差的BP网络预测
将GM(1,1)的预测值gm与实际值 y(0)m计算残差,并将该残差 εm与相关影响因素 x1、x2、x3、x4、x5作为训练数据对 BP 神经网络进行训练.网络结构为5-6-1,误差学习目标为0.0005,最大迭代次数为50000万,学习速度为0.07.隐含层和输出层的激活函数分别为tansig和purelin,训练函数为traingdx,利用Matlab7.0编程对BP模型进行训练,并对2007~2010年GM(1,1)预测残差进行仿真,预测结果如图4所示.
由图4可知,BP网络能够对GM(1,1)模型的工业废气排放量预测的残差进行高精度仿真.
将BP网络的残差仿真值与GM(1,1)模型的趋势预测值进行相加,作为南京市工业废气排放量的预测值.为增强对比性,分别采用时间序列预测(专家模型)、多元线性回归预测模型、GM(1,1)模型对2007~2010年南京市的工业废气排放量进行预测,预测的结果和误差分别如图5和表2所示.

图4 GM(1,1)残差的BP网络仿真结果
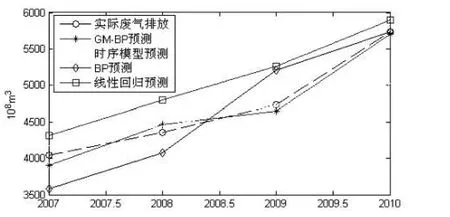
图5 GM-BP与其他模型预测结果对比
由图3、图5和表2可知,GM-BP的预测误差要远小于单一的GM(1,1)、BP网络模型及其他的传统模型.实验对比结果表明,GM-BP模型是一种高精度、有效的城市工业废气排放量预测模型,预测结果能够同时反映城市工业废气排放量的发展趋势和随机波动.
6 结束语
城市工业废气排放量呈现出复杂的非线性和随机性,很难建立准确的数学模型对其进行描述,而单一的线性模型或随机模型只能对城市工业废气排放量的部分信息进行描述,无法准确对其复杂非线性进行建模,导致预测精度较低.GM(1,1)模型具有很好的趋势预测能力,BP神经网络能够对非线性进行无限逼近.针对城市工业废气发展变化的特征,将GM(1,1)与BP进行交叉组合构建GM-BP预测模型,克服了单一GM(1,1)和BP模型的缺点,将二者的优点进行综合,从而提高预测精度.仿真结果表明,相对于单一城市工业废气排放量预测模型,GM-BP模型能同时兼顾数据序列的变化趋势性和波动性,具有更高的预测精度,能够应用于城市工业废气排放量预测.
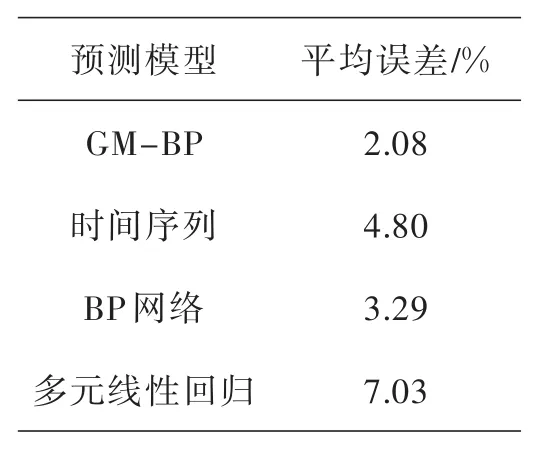
表2 各预测模型预测平均误差
[1]徐庆嫦.工业废气污染治理技术综述[J].广州化工,2012,40(15):186-187.
[2]沈楠.基于ARMA模型的湖南省工业废气排放量统计预测[J].中国商界,2009(9):212-213.
[3]汤鸣.西安市工业废气排放总量的灰色预测模型[J].西安航空技术高等专科学校学报,2009,27(5):46-48.
[4]卢伟真.城市交通废气污染现状及其预测方法[J].力学与实践,2008,30(4):1-7.
[5]郑敏敏,肖秀钦,陈庆华,等.福建省工业废气排放量的因子分析与灰色预测[J].环境科学与管理,2012,37(4):4-7.
[6]石为人,王燕霞,唐云建,等.基于灰色神经网络建模的水质参数预测[J].计算机应用,2009,29(6):1529-1531.
[7]刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].3版.北京:科学出版社,2004.
[8]LIN Chan-Ben,SU Shun-Feng,Yen-Tsen Hsu.High Precision Prediction Using Grey Models[J].Int J of Systems Science,2001,32(5):609-619.
[9]孙莉,翟永超.基于灰色BP神经网络的服装面料规格参数预测[J].计算机应用与软件,2012,29(7):154-156.
[10]朱世平,刘载文,王小艺,等.灰色理论与神经网络在水华预测中的应用[J].计算机工程与应用,2011,47(13):231-233.
[11]张雪伍,常晋义.PCA-BP在城市汽车保有量预测中的应用研究[J].计算机仿真,2012,29(12):376-379.

