考虑周期预防性维护的异速并行机集成调度研究

江才林，陆志强，崔维伟

（1.同济大学机械与能源工程学院，上海201804；2.上海交通大学机械与动力工程学院，上海200240）

考虑周期预防性维护的异速并行机集成调度研究

江才林1，陆志强1，崔维伟2

（1.同济大学机械与能源工程学院，上海201804；2.上海交通大学机械与动力工程学院，上海200240）

针对异速并行机系统，考虑机器具有周期预防性维护的不可用约束，建立生产调度与预防性维护集成优化的混合整数规划模型。基于改进LPT的机器负载均衡技术与基于最小装箱松弛法的单机调度优化算法，设计了有效的启发式算法HCA，与Cplex的数据试验比较表明，对于中小规模问题其解与最优解或低界的百分比误差小于10%。设计了结合装箱算法的混合遗传算法HGA，与HCA对比的数据试验表明，对于大规模问题HGA表现更加优异。通过与独立决策比较的数据实验证明了生产调度与设备维护的联合决策模型效果更优，可有效协调车间生产与维修的总体计划。

异速并行机调度；预防性维护；整数规划；启发式算法；混合遗传算法

生产实际中随着设备老化，机器需要预防性维护以改善机器性能或者故障后维修以恢复机器功能。由于定期执行预防性维护可降低设备发生意外故障的概率以提高系统的稳定性，近年来集成预防性维护策略的生产调度得到了研究者的普遍关注。根据计划期内维护的次数不同，研究主要分为2类：一类是在计划期内设备仅有一次维护，另一类是在计划期内设备需要进行多次周期性维护。对于第1类研究，针对单机系统，一般假设工件不可中断，研究各个不同调度目标如makespan等，提出各类启发式如SPT等并证明其误差边界或者设计分支定界等精确算法求解［1-3］。对于并行机系统，主要有各个机器需要同时进行预防性维护，或者其中一台进行预防性维护2种假设，求解方法为提出相应启发式算法［4-6］。对于第2类研究，针对单机系统，文献［7］考虑计划期内具有多个预防性维护，建立了整数规划模型。在此基础上，文献［8-12］研究了机器惰化效应，学习效应、计件维护以及柔性时间窗维护的拓展问题。文献［13］首先将维修成本、makespan、加权完成时间以及加权总延迟时间作为优化目标，采用多目标遗传算法进行优化。文献［14］考虑设备的失效函数，以总成本最小为目标。针对并行机系统，有学者分别研究了2台同型机和m台同型并行机的调度问题，并提出相应的改进启发式规则［15-16］。文献［17］则研究了的带有近似周期预防性维护的调度问题，目标为最小化最后一个维护活动的完成时间，证明其启发式算法的界小于2T＇／T。

从以上文献综述可以看到，考虑机器具有周期预防性维护的可用度约束，单机调度文献较多而并行机调度文献有限，且系统为同速并行机。实际车间中由于机器属性不同或机器新旧差异，导致其工件加工速率、预防性维护的周期以及维护所需时间均不同。本文旨在考虑异速并行机系统内各机器具有不同周期的周期性不可用约束，以最小化工件最大完工时间为目标，建立生产调度与设备维护的联合优化数学规划模型，并设计有效启发式算法对问题进行优化求解。

1 问题描述

将含有n个工件的工件集J＝｛J1，J2，…，Jn｝分配到m台机器M＝｛M1，M2，…，Mm｝上加工，目标为最小化工件的最大完工时间。所有工件在零时刻到达，工件基本加工时间为（i＝1，2，…，n），工件在加工过程中不允许中断；机器Mj加工速率为sj（i＝1，2，…，m），工件Ji的实际加工时间为＝／sj；机器需要周期性预防性维护，2次维护的间隔时间为Tj（i＝1，2，…，m），维护时间长度为tj（i＝1，2，…，m）。按照调度三元组表示法，问题可记为Qm／pm－nr／Cmax。图1为示例问题甘特图。

由于各个机器需要进行周期预防性维护，一个完整调度方案应包含工件的加工顺序和维护位置2个部分。若将2个预防性维护之间的工件集合称为一个批次，用Bjk表示机器j的第k加工批次的所有工件集合，则对应于这个批次的工件有其相应的开始时间以及完工时间。因此一个调度方案π是由m个子集πj（i＝1，2，…，m）构成，每个子集为工件批次集合和维护的组合πj＝（Bj1，PMj，Bj2，PMj…Bjkj），其中PMj代表机器j的维护时段，kj表示机器j的加工批次序号。用Pjk表示机器j的第k加工批次内所有工件的加工时间总和，用Gjk表示机器j的第k加工批次内的松弛时间，则有Gjk＝Tj－Pjk。

图1 考虑周期预防性维护的异速并行机调度示例Fig.1 An example of uniform machine scheduling with periodic maintenance

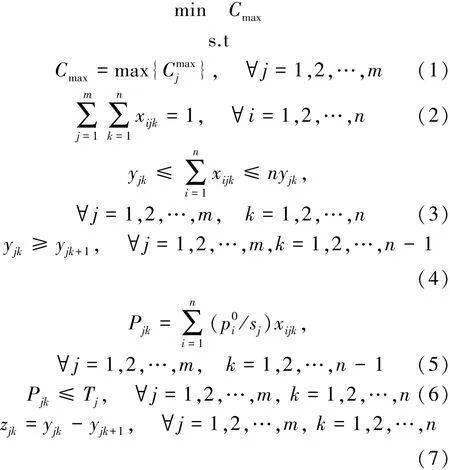
模型决策变量：xijk为0／1变量，如果工件i在第j机器第k加工批次加工，则取1，否则取0；yjk为0／1变量，如果机器j的第k加工批次有加工的工件，则取1，否则取0；zjk为0／1变量，如果机器j的第k加工批次为最后一个有加工工件实批次，则取1，否则取0。M为无穷大的正整数。约束（1）表示并行机系统的最大完工时间为所有机器完工时间的最大值；约束（2）表示每个工件仅由一台确定的机器加工一次；约束（3）表示若此批次有加工工件为“实批次”，则此批次的工件数量为1～n；约束（4）保证了当第j机器的第k加工批次为实批次，则之前的k－1加工批次也必为实批次；约束（5）、（6）表示分配到机器各个批次工件加工时间总和小于维护周期T；约束（7）、（8）表示当第j机器的第k加工批次为其最后一个实批次，则后续所有批次均为没有加工工件的“虚批次”；约束（9）表示每台机器至少存在一个实批次；约束（10）表示各个机器的最大完工时间由最后一个实批次的加工时间总和及其加工批次数量决定。

上述数学模型具有较好的扩展性，对于不同维护策略下的并行机调度问题，可通过相关变量的调整获得。例如，对于同速型的具有周期预防性维护的并行机调度问题Pm／pm－nr／Cmax只需要把约束（5）中的sj设置为1即可。

2 算法设计

由于此问题的强NP难性质，无法获得多项式时间的精确算法，虽可用Cplex等商用软件进行求解，但仅能求解小规模问题，无法在有效时间内解决大规模问题。本文提出基于改进LPT规则与最小装箱松弛法的构造型启发式算法HCA以及结合装箱算法的混合遗传算法HGA，可快速有效的解决此组合优化问题。

2.1 启发式算法HCA

由于机器具有可用度约束，本问题可以分解为2个子问题：1）工件分配即机器选择问题，应使得机器的负载均衡化。对于这类问题，当不考虑机器可用度时，LPT［1］规则为较好的启发式规则，其是指在零时刻将m个最长的工件分配到m台机器。此后，任一台机器空闲，剩下的工件中加工时间最长的将分配给这台空闲机器；2）当工件分配到机器后的单机工件排序问题。由约束（10）可知，机器Mj上，当机器具有最少加工批次以及最后加工实批次的工件加工时间最少时获得问题的最优解。由此，问题转化为变型的一维装箱问题。对于这类问题，由Gupta等提出的最小装箱松弛法（minimum bin slack，MBS）［18］采用递归方法在迭代的过程中不断减少非最后一个箱子的松弛量，使箱子的总数量减少的同时也降低最后一个箱子的容量。HCA首先通过改进LPT规则将工件均衡分配到各个机器上；继而将分配到机器的工件按照MBS规则重新排列使单机松弛时间最小，实现单台机器的局部优化；随后将每台机器的最后一批工件与其他机器的非最后一批工件进行交换，通过局域搜索实现各台机器间的平衡优化；最后将所有机器的最后一个加工批次的所有工件作为新工件集J＇，转化为没有可用度约束的小规模并行机调度问题并采用CPLEX求解，进一步均衡各台机器以提升解的质量。具体步骤如下：

1）生成初始调度方案。

①将工件集J按照加工时间长度降序排列，形成优先列表集合L＝｛J1，J2，…，Jn｝。

②将Ji按照列表L顺序逐一安排到能将其最先完工的机器上。即针对每台机器Mj，搜索工件Ji的最早允许加工时间为，并计算其完工时间，将工件分配到可以最早完工的机器上，生成一个初始调度方案π0＝｛，，…，｝。

2）对初始调度方案π0＝｛，，…，的每一个子集进行MBS重新排列得到一个新的调度方案π1＝｛，…，｝。

3）对新调度方案进行邻域交换以进一步改善。

①根据调度π1，机器Mj共包含kj个加工批次，集合记为Bj，Gjk为Mj的第k个批次的松弛时间。求得各机器的完工时间Cmjax，并记完工时间最长的机器为Ml。

②Ml的最后一个批次的工件数量为nl，并将工件按照加工时间降序排列，记J［i］为该批次的第i个工件。

③令i＝1。

④在机器集合｛M／Ml｝中，按照机器编号依次搜索机器Mj，在Mj中按照批次编号依次搜索各批次的最短加工时间工件J*，若交换J［i］、J*后不会违反Gjk约束，则交换两工件并转入⑤；若遍历结束之后没有交换成功，转入⑥。

⑤工件交换后，得到新调度π*，π*→π1，转入①。

⑥令i＝i＋1，若i≤nl，则转入④；否则转入步骤4）。

4）根据调度π1，将各台机器的最后一批工件取出，作为一个新的工件集J＇，将每台机器的前kj－1加工批次的结束时间作为机器的释放时间，此时转化为不带可用度约束的小规模纯调度问题，建立模型并导入Cplex求得最终解，算法结束。

为了进一步改善大规模下解的质量，本文设计了混合遗传算法HGA如2.2节所示。

2.2 混合遗传算法HGA

2.2.1 染色体编码与初始种群生成

选用实数编码，染色体的长度为n＋m－1，用－1～（－m＋1）作为划分不同机器的标识。图2为将9个工件分配到3台机器上加工的一条染色体示例。种群规模设为100，为保证种群多样性，采用随机生成的方法产生初始种群。

图2 编码示例Fig.2 An example of coding

2.2.2 解的改进

如图2所示，任一条染色体均包括m台机器的工件加工序列。对于机器Mj，预防性维护时间段已知，将各工件依次插入其最早允许加工的时间间隙内，可求得对应机器的最大完工时间。由2.1节子问题2可知，在工件分配到机器后该问题转化为变型的一维装箱问题，而MBS和降序首次适应算法（first fit decreasing，FFD）［15］均是较好的求解装箱问题算法，其中FFD是指将物品按照体积大小进行降序排列，然后按照顺序将物品放到第一个能装下它的箱子去。因此在GA的种群进化过程中，对每个新个体均执行如下Education操作，对个体进行改进。

Education：针对染色体中各个机器Mj（i＝1，2，…，m）的工件序列，将其所有工件分别按照FFD、MBS规则重新排列得到、，计算3个序列的Cmjax并取最小值的工件排序为最终序列πj，继而将所有机器的πj组合为新染色体。

2.2.3 遗传算子

由于本文采取实数编码方式，选择顺序交叉法对2个染色体进行交叉操作，选取互换变异进行变异操作。遗传算法中交叉概率一般取0.4～0.99，变异概率一般取为0.000 1～0.1。通过预实验调整，本算法选取交叉概率Pc＝0.8，变异概率Pm＝0.1。

2.2.4 适应度函数与种群进化机制

本文选取f（x）＝1／z作为适应度函数并进行指数尺度转换f＇（x）＝exp［（n＋m）f（x）］；通过轮盘赌方式进行选择操作，假设f（xi）为第i染色体的适应度值，染色体数量为N，则个体被选中的概率为；采用精英策略，使每一代最优个体能不参与交配直接保留下一代中。

3 仿真实验

本文运用优化软件ILOG CPLEX 12.1对线性整数规划模型进行求解，使用Visual C＃平台实现两类启发式算法，仿真环境为内存2.0 GB、主频2.1 GHz的便携式计算机。

3.1 算法验证

本文中，将2类算法结果Ch与最优解Co的百分比误差e＝（Ch－Co）·100／Co以及算法的运行时间作为指标来评估算法性能，并首先测试构造型启发式算法HCA的性能。考虑到不同问题规模以及参数设置可能对算法结果产生影响，参照文献［7］中的调度问题算例生成方法并进行适当调整，生成如下测试算例：工件规模n∈［20，30，50，100，200，500，1 000］；机器规模m∈［2，3，5，10，20，30，50］；工件的加工时间pi服从［10，30］的均匀分布；每种问题规模随机生成10组不同算例。在参数设置时，对于机器的加工速率参数分别设置sj∈［1.0，2.0］、sj∈［1.0，1.5］；预防性维护周期参数选取Tj设置；预防性维护时间长度参数也有tj＝Tj、tj＝Tj／5、tj＝Tj／10这3种设置，则共有18种参数设置。采用控制因子法，即在测试机器加工速率sj对算法影响时，对于每个sj将9种参数设置下共90个随机算例的平均值作为输出结果。同理，对于每个参数Tj、tj试验时分别将6种参数设置下的60组随机算例的平均值作为输出结果。数据测试结果如表1～3所示。

由表1～3可知，不同参数设置对启发式算法HCA结果影响甚微，算法百分比误差表现主要取决于问题规模的大小。在规模小于时50×5时该算法可以在运行时间小于2 s获得与最优解百分比误差在5%以内，当问题的规模达到200×10时，算法与CPLEX获得的低界的百分比误差接近10%。针对这一特点，本文提出了结合装箱算法的混合遗传算法对大规模问题下的解进一步改善。

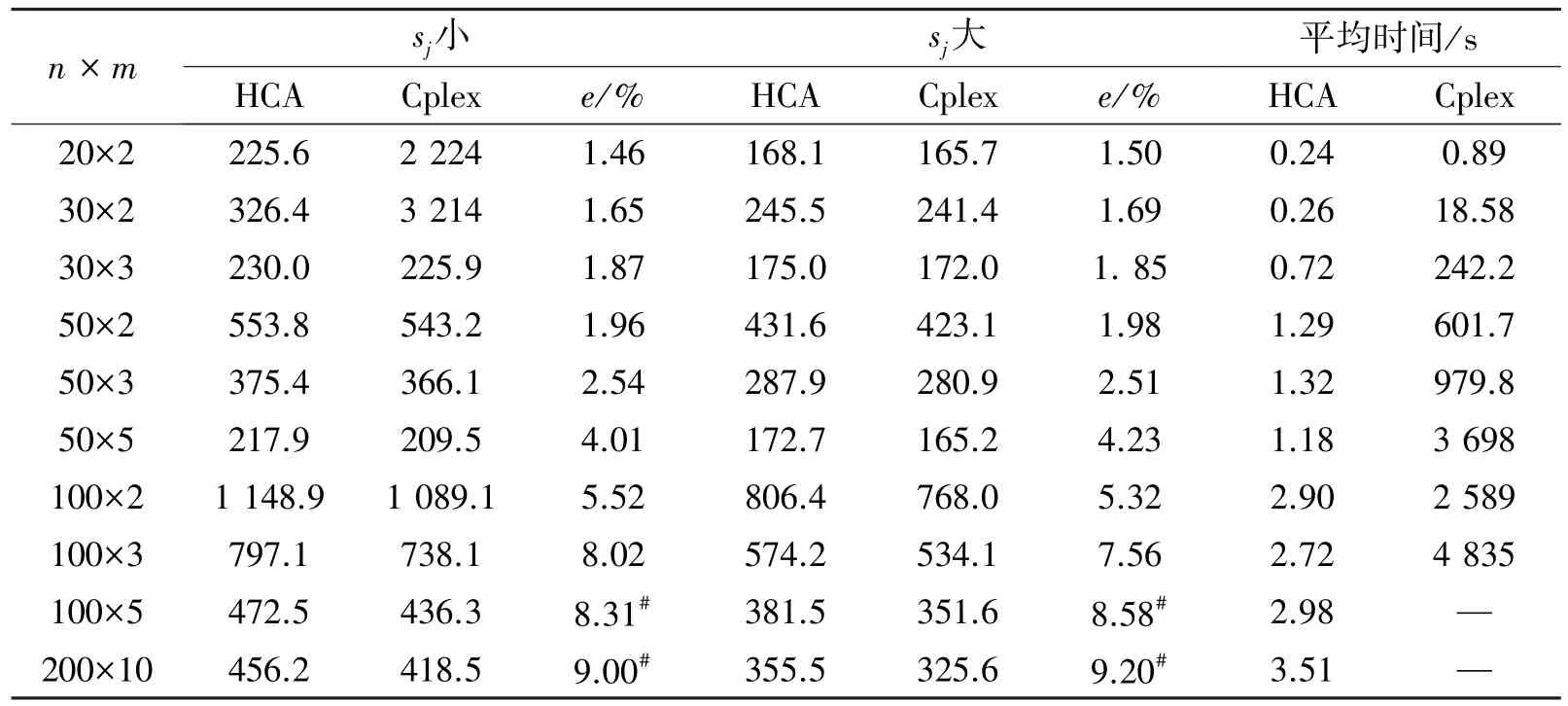
表1 不同机器速率sj设置下HCA算法性能表现Table 1 The performance of HCA algorithm under different sjsetting

表2 不同预防性维护周期Tj参数设置下算法HCA性能表现Table 2 The performance of HCA algorithm under different Tjsetting

表3 不同维护时间长度tj参数设置下算法HCA性能表Table 3 The performance of HCA algorithm under different tjsetting

表4 启发式算法HCA与混合遗传算法HGA比较Table 4 The comparison between heuristic HCA and improved genetic algorithm HGA

3.2 模型验证

生产实际中，生产计划与维护计划往往单独决策，首先采用传统的启发式规则如MULTIFIT［19］得到一个生产部分的工件加工顺序，继而依据预防性维护周期T，得到完整的调度方案。

表5 联合决策和单独决策的算法结果比较Table 5 The comparison between joint decision-making and independent decision-making

图3 联合决策方法相对于单独决策方法提升百分比GFig.3 The improvement of joint decision-making compared with independent decision-making

表5显示了各类问题规模下联合决策优化模型优化方法相对于单独决策模型优化方法的数据实验比较，可以看出联合决策模型的方法在牺牲少量运算时间的情况下可得到更优的解。图3显示了联合决策的优化方法HCA和HGA相对于单独决策的优化方法MULTIFIT的目标值提升百分比，可以看出随着问题规模的增大，联合决策的优化方法优势愈加明显，特别是HGA在问题规模为1 000×50时较单独决策的目标值提升超过22%。

4 结论

本文针对具有周期预防性维护的异速并行机集成调度问题进行研究，建立了相应的整数规划模型，得到结论如下：

1）Cplex软件能在可接受的时间内（2 h）对问题模型进行求解，获取工件与机器规模为50×5问题的最优解。

2）通过与求得的精确解或低界比较，表明本文提出的构造型启发式算法HCA能快速的求得中小规模问题的满意解，其GAP小于10%。而混合遗传算法HGA在求解大规模问题时效果更优，其解得到明显的改善。

3）与单独决策的调度模型相比较，集成预防性维护的联合决策方法较单独决策方法的优势明显，更有利于车间总体决策。

［1］LEE C Y.Machine scheduling with an availability constraint［J］.Journal of Global Optimization，1996，9（3）：395-416.

［2］MOSHEIOV G，SARIG A.Scheduling a maintenance activity to minimize total weighted completion time［J］.Computers and Mathematics with Applications，2009，57（4）：619-623.

［3］YANG S J.Minimizing total completion time on a single machine with a flexible maintenance activity［J］.Computers＆Operations Research，2011，38（4）：755-757.

［4］LIAO L W.Parallel machine scheduling with machine availability and eligibility constraints［J］.European Journal of Operational Research，2008，184（2）：458-467.

［5］RACEM M.Identical parallel machine scheduling under availability constraints to minimize the sum of completion times［J］.European Journal of Operational Research，2009，197（3）：1150-1165.

［6］TAN Z Y，CHEN Y.On the exact bounds of SPT for scheduling on parallel machines with availability constraints［J］.International Journal of Production Economics，2013，146（1）：293-299.

［7］CHOU J H，LOW C Y.A single-machine scheduling problem with maintenance activities to minimize makespan［J］.Applied Mathematics and Computation，2010，215（11）：3929-3935.

［8］XUEP F.Single machine scheduling with piece-rate maintenance and interval constrained position-dependent processing times［J］.Applied Mathematics and Computation 2014，226：415-417.

［9］LEE J Y.Minimizing the number of tardy jobs in a single-machine scheduling problem with periodic maintenance［J］.Computers＆Operations Research，2012，39（9）：2196-2205.

［10］YANG S J.Single-machine scheduling problems simultaneously with deterioration and learning effects under deteriorating multi-maintenance activities consideration［J］.Computers＆Industrial Engineering，2012，62（1）：271-275.

［11］蒋志高，董明.考虑维护且加工时间可变的单机调度问题研究［J］.工业工程与管理，2011，16（3）：68-74.JIANG Zhigao，DONG Ming.Study on single machine problem with maintenance and variable processing time［J］.Industrial Engineering and Management，2011，16（3）：68-74.

［12］CHEN J S.Scheduling of non-resumable jobs and flexible maintenance activities on a single machine to minimize makespan［J］.European Journal of Operational Research，2008，190：90-120.

［13］金玉兰，蒋祖华.预防性维修计划和生产调度的多目标优化［J］.哈尔滨工程大学学报，2011，32（9）：1205-1209.JIN Yulan，JIANG Zuhua.Multi-objective optimization research on preventive maintenance and production scheduling［J］.Journal of Harbin Engineering University，2011，32（9）：1205-1209.

［14］崔维伟，陆志强.单机系统的生产调度与预防性维护的集成优化［J］.上海交通大学学报，2012，46（12）：2009-2013. CUI Weiwei，LU Zhiqiang.Integrating production scheduling and preventive maintenance planning for a single machine［J］.Journal of Shanghai Jiaotong University，2012，46（12）：2009-2013.

［15］SUN K B.Scheduling problems with multiple maintenance activities and non-preemptive jobs on two identical parallel machines［J］.International Journal of Production Economics，2010，124（1）：151-158.

［16］程贞敏，李洪兴.最小化时间表长的平行机调度近似算法研究［J］.北京师范大学学报，2012，48（1）：11-15.CHENG Zhenmin，LI Hongxin.Approximated algorithm for identical machine scheduling with minimized makespan［J］.Journal of Beijing Normal University，2012，48（1）：11-15.

［17］XU D H.Parallel machine scheduling with almost periodic maintenance and non-preemptive jobs to minimize makespan［J］.Computers＆Operations Research，2008，35（4）：1344-1349.

［18］GUPTA J N D.A new heuristic algorithm for the one-dimensional bin-packing problem［J］.Production Planning＆Control，1999，10（6）：598-603.

［19］BURKARD R E.A note on MULTIFIT scheduling for uniform machines［J］.Computing，1998，61（1）：277-283.

Integrated uniform machine scheduling with periodic preventive maintenance

JIANG Cailin1，LU Zhiqiang1，CUI Weiwei2
（1.School of Mechanical and Energy Engineering，Tongji University，Shanghai 201804，China；2.School of Mechanical and Power Engineering，Shanghai Jiaotong University，Shanghai 200240，China）

A mixed integer programming model integrating the production scheduling and preventive maintenances is proposed to solve the unavailability constraints of uniform machine scheduling system problem.Specifically，a constructive heuristic algorithm（HCA）has been developed based on load balancing technology of improved longest processing time（LPT）rule and single machine optimization method of minimum bin slack heuristic.The numerical experiment compared with Cplex showed that the gap between the solution of HCA and optimal solution（low bound）is less than 10%for the small and medium scale problems.Furthermore，a hybrid genetic algorithm（HGA）combining bin-packing algorithm is proposed.The numerical experiment compared with HCA showed that the performance of HGA is better than HCA for large scale problems.Finally，the data experiments indicated that the joint decision-making model integrating production scheduling and machine maintenance appears to perform better than the independent decision-making model，as well as coordinate the overall plan of the production and maintenance effectively.

uniform machine scheduling；preventive maintenance；integer programming；heuristic algorithm；hybrid genetic algorithm

10.3969／j.issn.1006-7043.201307059

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201307059.html

F224

A

1006-7043（2014）11-1409-06

2013-07-22.网络出版时间：2014-09-25.

国家自然科学基金资助项目（71171130）；上海市自然科学基金资助项目（12ZR1414400）.

江才林（1989-），男，硕士研究生；陆志强（1968-），男，教授，博士生导师.

陆志强，E-mail：zhiqianglu＠tongji.edu.cn.