多自由度微陀螺结构参数对其动态性能影响分析

郝燕玲，刘博，胡钰

（哈尔滨工程大学自动化学院，黑龙江哈尔滨150001）

多自由度微陀螺结构参数对其动态性能影响分析

郝燕玲，刘博，胡钰

（哈尔滨工程大学自动化学院，黑龙江哈尔滨150001）

为了解决多自由度微机械陀螺结构设计中存在的参数耦合问题，提出了一种基于增益和带宽最优化的参数设定方法。为了从结构设计和参数限定的角度提高单轴微机械振动陀螺的性能指标，分析了多自由度单轴微机械振动陀螺的参数对于陀螺性能的影响。为了抑制低频环境噪声对于输出信号的影响，陀螺的驱动需要在高频率范围内进行操作。通过理论推演得到在高操作频率下陀螺结构设计中广泛存在于峰值间隔频率、操作频率、阻尼与陀螺性能之间相互制约的内在关系。结合其设计原则，设计出的微机械陀螺带宽为200 Hz、增益提高了5 dB，能满足绝大多数工程应用的要求。关键词：多自由度；微机械陀螺；峰值间隔频率；操作频率；空气阻尼

微机械陀螺以其体积小、重量轻、成本低、可靠性高等特点，在近年来受到了众多科研人员的关注［1］。在微机械陀螺的结构设计中主要考虑的问题是敏感度和带宽，以及对环境变化的鲁棒性。

传统设计采用单自由度振动系统，每个模态具有各自的共振频率。理论上在真空中，当驱动模态和敏感模态的共振频率相互匹配时，陀螺的机械敏感度达到最大［2］。虽然这种严格匹配的方式能够获得理想的陀螺敏感度，但是获得的系统带宽却十分狭窄。实际制造中，通常采用驱动模态共振频率和敏感模态共振频率具有一定的频率差的近似匹配的方式来增大陀螺带宽，所以陀螺的操作方式和最终性能取决于两模态的相对位置［2-4］。然而这种模态匹配的设计方式以牺牲带宽为代价提高增益，并且陀螺性能易受到结构参数和环境变化的影响，需要通过增加模态的机械自由度的方式增强陀螺的鲁棒性［5-7］。在改进微机械陀螺结构设计过程中，通过增加陀螺的机械自由度来提升陀螺带宽和稳定性是十分关键的一步［8-9］。多自由度振荡结构已经被引入驱动模态用于提升陀螺的稳定性。典型的自动控制操作环境中，需要提升操作频率来抑制环境噪声对陀螺输出的影响［2-3］。

本文为了解决在大气压环境中，陀螺结构参数的耦合关系与高性能陀螺机械参数选取的问题。在高操作频率的条件下，分析了阻尼、峰值间隔频率、操作频率等参数对于系统性能的影响，并基于上述分析将二自由度振荡结构同时引入驱动模态和敏感模态设计了满足实际工程要求的陀螺系统。

1 多自由度微机械陀螺

1.1 工作原理与结构

如图1所示，驱动质量m1与解耦质量mf受到设置在驱动质量两侧的驱动电极产生的沿x方向的谐振正弦力Fd的激励，在驱动方向做单自由度振动。由于单自由度弹性悬梁k4、k5的限制，迫使转换质量m2和检测质量m3随解耦质量mf沿x方向振动。当陀螺有垂直于x-y平面的外部旋转角速度Ωz输入时，会在转换质量和检测质量上产生沿y方向科里奥利力FC1＝－2m2x·2ΩZ、FC2＝－2m3x·2ΩZ。在科里奥利力的作用下在y方向上转换质量m2和检测质量m3产生了相对解耦质量mf的振动。通过对于安放在检测质量内的电极进行检测，可以反映出科里奥利力的大小，进而得到旋转角速度Ωz。

图1 微机械陀螺结构图Fig.1 Schematics of the MEMS gyroscope

图2 描述的是陀螺简化集成动力学模型，与传统微机械陀螺设计不同：在驱动模态采用完全二自由度系统，敏感模态采用二自由度动力消振器结构。

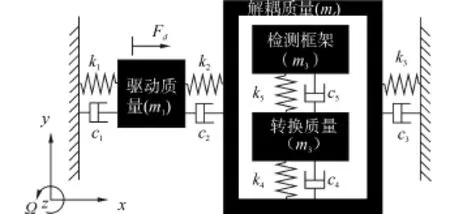
图2 微机械陀螺动力学模型Fig.2 Lumped dynamics model of the MEMS gyroscope

1.2 多自由度系统动态模型

根据图1、2的微机械陀螺结构，可以得到理想系统的动力学方程：

式中：x1、x2表示驱动质量和解耦质量在驱动方向上的位移，y1、y2表示转换质量和检测质量相对于解耦质量在敏感方向上的位移；c1、c2、c3表示驱动质量和解耦质量在驱动方向上受到的阻尼，c4、c5表示解耦质量和检测质量在敏感方向上受到的阻尼；k1、k2、k3、k4、k5分别表示对应位置弹性悬梁的刚度；Fd为简谐驱动力，FC1、FC2分别为敏感方向上作用在m2、m3上的科里奥利力。

在式（1）、（2）中，由于Fd的操作频率选取为几千赫兹远远大于输入角速度Ωz变化频率（小于10 Hz）。

传统单自由度敏感模态陀螺，设计的关键参数是驱动模态和敏感模态的共振频率，这是由于驱动模态和敏感模态的共振频率的相对位置决定了陀螺最终的增益和输出［10］。而多自由度陀螺由于引入了额外的质量块，其机械特性主要取决于3个频率：操作频率ωd、敏感模态低共振频率ωL、敏感模态高共振频率ωH。驱动模态和敏感模态被设计成相同的操作频率（ωd＝ωs），因此二自由度敏感模态的结构设计是关注的重点，特别是获得实现所期望敏感模态共振频率ωL、ωH所需要的k4、k5、m2和m3等结构参数的取值。

二自由度敏感模态存在结构耦合，且操作频率需要设定在2个共振频率的平坦区域之间，所以操作频率、敏感模态高、低共振频率的选定并不是相互独立的。

从式（2）求得敏感模态的结构频率：

式中：ω1和ω2表示m2和m3两端均固定时的固有结构频率，ω3表示两质量块之间的耦合［11］。利用等式（3），得到二自由度敏感模态特征方程：

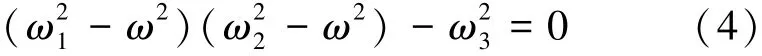
求解上式，得敏感模态增益最大的共振频率：

式中：ωH、ωL是由结构频率ω1、ω2和ω3确定的高、低共振频率。操作频率位于两共振频率中间，共振频率的差值为敏感模态的峰值间隔频率：

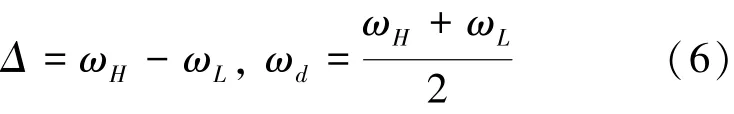
式中：ωd是操作频率、Δ是敏感模态的峰值间隔频率。在系统的结构频率ω2、ω3存在耦合（＝）：

式中：比例因子ε表示敏感模态两质量块的质量比，也是反映ω2、ω3之间的耦合关系的重要系统参数。把式（7）代入式（5），可以得到

式中：二自由度敏感模态结构频率ω1、ω2可以表示成关于操作频率ωd、峰值间隔频率Δ和比例因子ε的设计方程。弹性悬梁弹力值可以通过式（8）、（9）计算得到。

2 性能分析

增加陀螺的自由度可以在2个峰值频率之间提供一个增益近似为常值的带宽区域［12］，这种采用多自由度振荡系统来拓展带宽的方法必然会以牺牲系统的增益为代价，同时增加了分析阻尼、操作频率、峰值间隔频率对陀螺特性影响的复杂程度［13］。以获得高增益和宽带宽为设计目的，下面对阻尼、操作频率和峰值间隔频率对敏感模态的影响进行分析。

2.1 阻尼对敏感模态的影响

动力学方程组（1）、（2）表示陀螺驱动模态和敏感模态的运动特性。在简谐力Fd的激励下，系统的位移均按照正弦规律变化，由拉普拉斯变换可以求出Y2的稳态解：

将s＝jω代入式（10），得到检测位移稳态解Y2（s）的频域表达式：

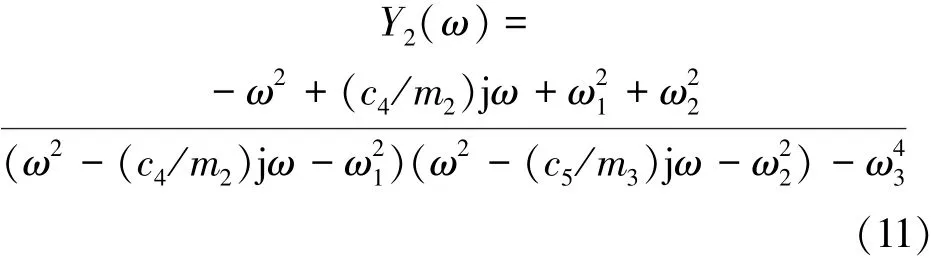
式中：分母为系统方程的特征多项式Δs（ω）＝（ω2－（c4／m2）jω－ω21）（ω2－（c5／m3）jω－ω22）－ω43。检测质量块位移的稳态解Y2（ω）用于后续阻尼对敏感模态频率响应影响的分析和仿真。

2.2 敏感模态的增益和带宽

驱动模态和敏感模态被设计成二自由度振荡系统，在模态的2个峰值频率之间产生具有稳定响应的区域，使得陀螺频率响应曲线在较宽范围内保持幅值稳定。虽然增加自由度提高了陀螺响应的稳定性，但是陀螺敏感模态的参数选取也变得更为复杂也更为灵活，针对这个问题需要对敏感模态参数对陀螺性能的影响进行分析。二自由度系统在零阻尼条件下具有最大的增益和最小的带宽［14-20］，为了推导操作频率和峰值间隔频率对系统增益和带宽的限制条件，在零阻尼条件下对方程组（2）进行求解，由拉普拉斯变换可以得到系统的传递函数：

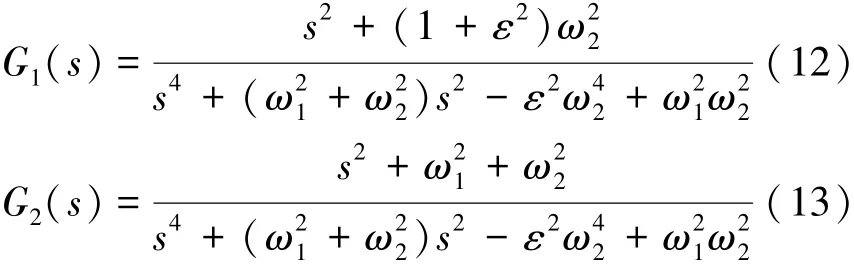
陀螺性能主要取决于检测质量的响应特性，以下着重对检测质量的位移G2（s）进行分析。将式（8）、（9）代入式（13），同时令s＝jω可以得到

上式描述了检测质量对于不同频率的响应，反映了多自由度陀螺敏感模态增益随驱动频率变化情况。当驱动频率与设定的操作频率相等时，G2（ωb）的值决定了在实际操作频率下陀螺的标度因子。将ω＝ωd代入式（14）得

从上式可以看到，当陀螺系统在预定的操作频率下工作时，敏感模态的增益是只包含峰值间隔频率和操作频率的多项式。在实际设计中，操作频率ωd为几千赫兹量级、峰值间隔频率Δ为几百赫兹级，所以式（15）可以近似化为

在二自由度振荡系统中，当驱动频率等于峰值频率时，系统的增益达到最大。操作频率位于2个峰值频率中间，可以近似认为在带宽范围内对应的增益最小。敏感模态带宽范围定义在增益比最小值提高3 dB的频率范围内。

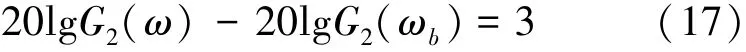
求解方程（17）可以得到带宽的边界频率，带宽即为两边界频率之差：

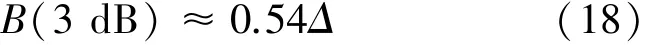
3 参数的选取和仿真验证

3.1 结构参数的选取

为了验证本文提出的多自由度微机械振动陀螺参数对其性能的影响分析方法，同时设计一种综合考虑陀螺敏感性和鲁棒性的陀螺结构，按照性能特征和结构参数的内在联系选取了机械结构参数。

为了获得敏感模态弹性悬梁的表达式，将式（3）代入式（8）、（9）可以得到

从式（19）、（20）可以看出，弹性悬梁的弹力值选取和操作频率ωd、峰值间隔频率Δ和比例因子ε有关，当选取比例因子为ε＝0.71时，通过确定质量块的质量，计算出陀螺敏感模态结构参数值。

与敏感模态类似建立驱动模态动态方程可以确定出驱动模态各弹性悬梁的弹力值：

式中：Δd为驱动模态的峰值间隔频率，反映了陀螺驱动模态的带宽大小。为了使得陀螺有更长的使用寿命和更简单的加工工艺，设定陀螺工作在空气中。微机械陀螺的机械结构参数见表1。

表1 微机械陀螺阵列的参数选择Table 1 Parameters setting of proposed gyroscope array

3.2 参数限制条件的频域特性验证

根据表1选取的参数值建立微机械振动陀螺模型，并针对在高操作频率ωd的条件下，验证对于峰值间隔频率Δ、阻尼c对于陀螺性能影响的分析。

图3描述了微机械陀螺工作环境从零阻尼到空气阻尼变化时敏感模态的频率响应曲线，从响应结果可以看出，在操作频率5 kHz周围阻尼变化对于频率响应的增益影响不大（小于2 dB），当靠近峰值频率时，响应的增益变化剧烈（最大波动约为40 dB）。选取预设操作频率ωd为驱动频率时，增益对于阻尼的变化具有很强的鲁棒性。

图4为在空气阻尼环境中，不同峰值间隔下敏感模态的频率响应。随着峰值间隔频率的减小，频率响应的3 dB带宽减小、增益变大。当峰值间隔频率小于250 Hz时，由于空气阻尼的作用敏感模态增益变化受到强烈的抑制，然而带宽仍在减小。所以，选取峰值间隔频率为250 Hz时，敏感模态具有高增益同时保持了较大的带宽。

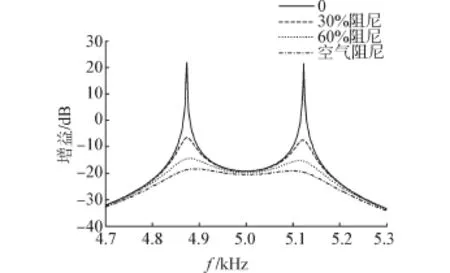
图3 不同阻尼下敏感模态的频率响应Fig.3 Frequency responses for damping in sense-mode

图4 不同峰值间隔频率下敏感模态的频率响应Fig.4 Frequency response of different peak spacing in sense-mode

图5 敏感模态的频率响应Fig.5 Frequency response of sense-mode

由上述分析，选取操作频率ωd＝5 kHz和峰值间隔频率Δ＝250 Hz，图5对比了按照前文确定的参数选取原则设计的新参数结构和经验公式设计的传统微机械陀螺敏感模态频率响应特性。从图中可以看到，新结构设计增益比传统设计提高了约5 dB，带宽为4.84～5.15 kHz之间的310 Hz。

陀螺性能由驱动模态和敏感模态共同决定，驱动模态也采用二自由度振荡结构。图6为单自由度和二自由度驱动模态幅频特性曲线。如图所示，二自由度敏感模态在4.89～5.09 kHz之间提供了200 Hz的3 dB带宽。在空气环境中，通过适当设置微机械陀螺的机械结构参数可以使二自由度驱动模态的增益达到与单自由度相当的程度，与单自由度驱动模态相比带宽大幅度提高了3倍。

图6 驱动模态的频率响应Fig.6 Frequency response of drive-mode

结合图5、6可以看出，驱动模态和敏感模态的操作频率相互匹配，最终陀螺以5 kHz为中心频率整体带宽为200 Hz，增益提高了约5 dB。

4 结论

通过假设系统在零阻尼条件下振动，求解出最大增益和最小带宽的表达式。当操作频率远高于峰值间隔频率时，推导出增益和带宽与操作频率的取值无关的结论。在陀螺结构设计中，增益和带宽存在着相互制约的关系：当敏感质量比一定时，敏感模态增益随着峰值频率间隔的增大而减小。通过求解多自由度动力学振动方程，建立系统的操作频率、峰值间隔频率、阻尼与陀螺系统频率响应关系，可以在空气阻尼的环境中设计出增益响应特性与单自由度陀螺相当、带宽扩展3倍的驱动模态。本设计可以应用于稳定性要求更为苛刻的环境中，并且为多自由度陀螺结构的参数选取指明了方向。

［1］WANG W，LYU X Y，SUN F.Design of a novel MEMS gyroscope array［J］.Sensors－Open Access Journal，2013，13：1651-1663.

［2］WEINBERG M，KOUREPENIS A.Error sources in in-plane silicon tuning-fork MEMS gyroscopes［J］.IEEE／ASME Journal of Microelectromechanical Systems，2006，15：479-491.

［3］NEUL R，GOMEZ U M，KEHR K，et al.Micromachined angular rate sensors for automotive applications［J］.IEEE Sensors Journal，2007，7（2）：302-309.

［4］GEEN J A，SHERMAN S J，CHANG J F，et al.Single-chip surface micromachined integrated gyroscope with 50 deg／h Allan deviation［J］.IEEE Journal of Solid-State Circuits，2002，37（12）：1860-1866.

［5］ACAR C，SHKEL A.Inherently robust micromachined gyroscopes with 2-DOF sense-mode oscillator［J］.IEEE／ASME Journal of Microelectromechanical Systems，2006，15（2）：380-387.

［6］SCHOFIELD A R，TRUSOV A A，ACAR C，et al.Antiphase driven rate gyro-scope with multi-degree of freedom sense mode［C］／／Proceedings of the 14th International Conference on Solid-State Sensors，Actuators and Microsystems（TRANSDUCERS'07）.Lyon，France，2007：1199-1202.［7］SCHOFIELD A R，TRUSOV A A，SHKEL A M.Multi-degree of freedom tuning fork gyroscope demonstrating shock rejection［C］／／Proceedings of the IEEE Sensors.Atlanta，USA，2007：120-123.

［8］ACAR C，SHKEL A.Nonresonant micromachined gyroscopes with structural mode-decoupling［J］.IEEE Sensors Journal，2003，3（4）：497-506.

［9］JEON S H，LEE J Y，JUNG H K，et al.Two-mass system with wide bandwidth for SiOG（silicon on glass）vibratory gyroscopes［C］／／Proceedings of International Conference of Solid State Sensors and Actuators Microsystem.Seoul，Korea，2005：539-542.

［10］WEINBERG M，KOUREPENIS A.Error sources in inplane silicon tuning-fork MEMS gyroscopes［J］.Microelectromechine System，2006，15（3）：479-491.

［11］SCHOFIELD A R，TRUSOV A A，SHKEL A M.Micromachined gyroscope concept allowing interchangeable operation in both robust and precision modes［J］.Sensors Actuators A：Physical，2011，165：35-42.

［12］SCHOFIELD A R，TRUSOV A A，SHKEL A M.Inherently robust micromachined gyroscopes with 2-DOF sensemode oscillator［J］.Journal of Microelectromechanical Systems，2006，15（2）：380-387.

［13］SCHOFIELD A R，TRUSOV A A，SHKEL A M.Effects of operational frequency scaling in multi-degree of freedom MEMS gyroscopes［J］.IEEE Sensors Journal，2008，8（10）：1672-1680.

［14］SAHIN K，SAHIN E，ALPER S E，et al.A wide-bandwidth and high-sensitivity robust microgyroscope［J］.Journal of Micromechanics and Microengineering，2009，19（7）：1722-1726.

［15］WANG W，LYU X Y，SUN F.Design and simulation of micromachined vibratory gyroscope with two degree-of-freedom drive-mode and sense-mode［J］.IEEE Sensor Journal，2012，12：2460-2464.

［16］郝燕玲，刘博，史宏洋.新型反相位驱动双解耦微机械陀螺设计［J］.哈尔滨工业大学学报，2014，46（9）：105-109.HAO Yanling，LIU Bo，SHI Hongyang.The novel design of anti-phase double-decoupled micromachined gyroscope［J］.Journal of Harbin Institute of Technology，2014，46（9）：105-109.

［17］李小卿，常洪龙，焦文龙，等.基于杠杆的微机械陀螺结构设计与仿真［J］.微纳电子技术，2012，49（5）：313-317.LI Xiaoqing，CHANG Honglong，JIAO Wenlong，et al.Structure design and simulation of the MEMS gyroscope based on leverage mechanism［J］.Micronanoelectronic Technology，2012，49（5）：313-317.

［18］郝燕玲，刘博，周广涛.高敏感度微机械陀螺阵列的设计［J］.华中科技大学学报：自然科学版，2014，42（3）：42-46.HAO Yanling，LIU Bo，ZHOU Guangtao.Design of a MEMS gyroscope array with high sensitivity［J］.Journal of Huazhong University of Science and Technology：Nature Science，2014，42（3）：42-46.

［19］张峰，苑伟政，常洪龙，等.静电梳齿驱动结构的稳定性分析［J］.传感器技术学报，2011，24（8）：1122-1125.ZHANG Feng，YUAN Weizheng，CHANG Honglong，et al.Analysis of lateral stability of electrostatic comb-drive structure［J］.Journal of Transduction Technology，2011，24（8）：1122-1125.

［20］成宇翔，张卫平，陈文元，等.MEMS微陀螺仪研究进展［J］.微纳电子技术，2011，48（5）：277-285.CHENG Yuxiang，ZHANG Weiping，CHEN Wenyuan，et al.Research development of MEMS micro-gyroscopes［J］.Micronanoelectronic Technology，2011，48（5）：277-285.

Analysis of the influence of the multiple degree of freedom MEMS gyroscope structural parameters on the performance

HAO Yanling，LIU Bo，HU Yu
（College of Automation，Harbin Engineering University，Harbin 150001，China）

To solve the problem of structural tradeoff in multiple degrees of freedom（DOF）micro electro mechanical systems（MEMS）gyroscopes，the method of global optimization of gain and bandwidth is provided in this paper.To improve the performance of the MEMS vibratory gyroscopes from the structural design and the limitation of the parameters，the influence of parameters on the performance of the gyroscopes is analyzed.To reduce the effect of the low-frequency environmental noise on the output signal，the gyroscope needs to be driven in the high frequency region.The internal relationships between peak spacing frequency，operating frequency，damping and the performance of the gyroscope were derived by precise theoretical calculations.The proposed gyroscope is designed with the bandwidth of 200 Hz and the gain is increased by 5 dB，which can satisfy the requirements of most practical applications.

multiple degrees of freedom；micro electro mechanical systems（MEMS）；peak spacing；operational frequency；damping

10.3969／j.issn.1006-7043.201307003

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201307003.html

U666.12

A

1006-7043（2014）11-1378-06

2013-07-05.网络出版时间：2014-09-18.

国家自然科学基金资助项目（61203225）；中国博士后科学基金面上资助项目（2012M510083）.

郝燕玲（1944-），女，教授，博士生导师.

郝燕玲，E-mail：haoyanling＠herbeu.edu.cn.