Dieterici方程在CO2中的J-T效应

陈 漓，莫小梅

（百色学院 a.物理与电子工程系；b.化学与生命科学系，广西 百色 533000）

节流膨胀产生的效应也称为J-T效应，J-T效应的研究对于低温制冷技术具有重要意义.对于气体的J-T效应，文献[1]运用vdW方程讨论CO2气体J-T效应，只是在定性上符合.文献[2]用CO2气体分子模型讨论转换曲线，文献[3]运用Dieterici方程讨论氮气的转换温度.本文我们以Dieterici状态方程讨论CO2气体的J-T效应，在定性的基础上进一步定量分析J-T系数和转换温度，并与实验值进行比较分析.

1 J-T系数 μJT

气体经节流膨胀后的温度变化与压强变化的比值为节流膨胀系数，也称为J-T系数，通过节流膨胀实验可以测定J-T系数.由于节流膨胀为等焓过程，运用热力学函数关系可以得到

上式确立了J-T系数μJT、定压比热容Cp和状态方程三者之间的关系.为了方便计算J-T系数的数值，，代入（1）式可得

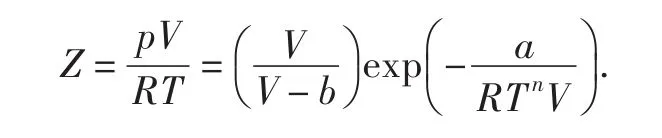
上式包含有Z因子Dieterici方程，为进一步推导出J-T系数与温度和压强的关系，我们把上式按Virial方程（Leiden型）形式进行展开[5]，以T，V为变量得到：，其中

也可以把含有Z因子Dieterici方程以Virial方程另一种形式（Berlin型）展开，即以T、p为变量，得到：其中

通过对Virial方程Leiden型和Berlin型展开式进行比较，可以得到Dieterici方程的一个等效的（Berlin型）Z表达式.

把上式代入（2）式，在低压或中等压强情况下，对上式的压强高次项可进行截断，得到Dieterici气体计算J-T系数 μJT的关系式为

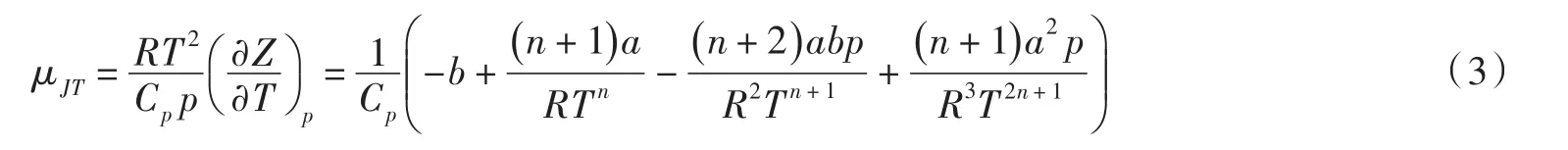
温度指数n可以分别取1，1.2，1.4，1.5，1.6等数值，代入（3）式可以计算出在一定压强下CO2J-T系数μJT随温度变化的理论值（见表1），与CO2J-T系数 μJT的实验值相比较.CO2J-T系数 μJT的实验值引用文献[7].

由表2数据可以看出当n=1.5时，μJT的实验值与Dieterici气体理论值平均误差为12.56%，总体吻合的较好.比vdW气体理论值偏差更小[1].

表1 定压摩尔热容计算常数表（标准差S=0.0004613，相关系数R=0.9999897）

2 转换温度和转换曲线

由于J-T系数可正可负，当J-T系数等于零时，可以在压强和温度的关系图上绘制出一条曲线，即J-T效应的转换曲线，所得到的对应温度为转换温度.

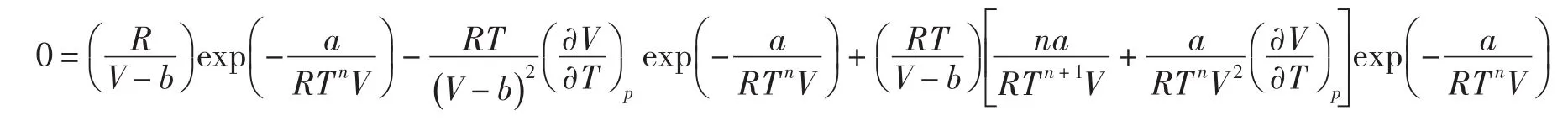
表2 CO2的J-T系数 μJT（压强 p=1.013×105Pa）

整理得

代入（1）式，当 μJT=0，整理后得

把上式结果代入Dieterici气体状态方程求解，得转换温度T与压强p的关系式

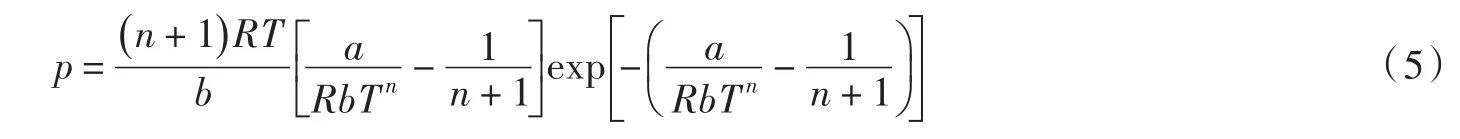
上式即为由Dieterici气体状态方程推导出的转换温度与压强关系的转换曲线方程式.

利用Dieterici气体转换曲线方程式可求出转换曲线的一些特征值.当压强趋于零时，可求出Dieterici气体最大转换温度和最小转换温度.即 p→0时，最大转换温度最小转换温度Tmin→0.

运用给定的CO2的Dieterici气体常数a、b和R的数值代入上述的结论可以得Dieterici气体的特征值.改变引力项的温度指数n，计算出CO2转换曲线的理论特征值，并与文献[7]实验值比较（见表3）.应用Matlab软件绘制CO2转换曲线的T—p图，如图1所示.

从图1的对比结果可看出，Dieterici状态方程的温度指数n=1时与实际结果偏离很大，而当Dieterici状态方程的温度指数取值n=1.5或1.6时，得到的CO2气体转换曲线与实验测定的CO2气体转换曲线有较好的吻合，且随着温度的下降，误差逐渐的缩小，尤其是温度在小于 500 K，压强小于 850×105Pa时Dieterici的CO2气体转换曲线理论值与实验值符合的好.而vdW状态方程得到CO2气体转换曲线与实验有较大的偏差.

表3 CO2转换曲线特征值T,p

3 结论

运用Dieterici方程能比较客观地反映气体的J-T效应的各种基本关系，在定量上也具有一定的指导意义.Dieterici状态方程在考虑分子间的引力时采用了指数因子来表示，显示出比vdW方程更贴近实际气体的行为和热力学性质.因此，目前有不少三参数和多参数状态方程也引入指数因子进行修正，得到了比较满意的结果.

图1 CO2气体的转换曲线

[1]莫小梅.CO2气体等焓膨胀的焦耳－汤姆逊效应[J].百色学院学报，2010（6）：96-100.

[2]Chacin A,Muller E.A,Vazquez J M.Molecular simulation of the Joule-Thomson inversion curve of carbon dioxide[J].Fluid Phase Equilibria,1999,165(2):147-155

[3]赵汝顺.Dieterici实际气体转换温度的研究[J].沈阳工业大学学报，2010（2）：236-238.

[4]陈宏芳，杜建华.高等工程热力学[M].北京：清华大学出版社，2003：99.

[5]William A.Parkinson.Second-and Higher-Order Virial Coefficients Derived from Equations of State for Real Gases[J].Journal of Chemical Education,2009,86(1):112-115.

[6]Span R,Wagner W.A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple-Point Temperature to 1100 K at Pressures up to 800 MPa[J].Journal of Physical and Chemical Reference Data,1996(25):1509-1596.

[7]Robert H Perry.Perry’s Chemical Engineers’Handbook[M].New York:McGraw-Hill Companies,1999:2-134.