复合假设下导弹可靠性指标Bayes检验方法
甄 昕,丁力军
(1.解放军92941部队93分队,辽宁 葫芦岛 125000;2.解放军92493部队98分队,辽宁 葫芦岛 125000)
复合假设下导弹可靠性指标Bayes检验方法
甄 昕1,丁力军2
(1.解放军92941部队93分队,辽宁 葫芦岛 125000;2.解放军92493部队98分队,辽宁 葫芦岛 125000)
在用Bayes方法对海防战术导弹可靠性指标进行假设检验时,原假设和对立假设均采用简单假设的形式,而此种方法可能导致使用方Bayes风险增大。从理论上阐述了简单假设Bayes检验方法可能导致使用方Bayes风险增大的原因,同时给出了用于取代简单假设的复合假设Bayes检验方法,并用实例证明了它比简单假设Bayes检验方法科学、合理。
简单假设,复合假设,经典风险,Bayes风险
引言
从上世纪90年代开始,Bayes理论逐渐在海防战术导弹试验与鉴定领域得到应用,主要应用在导弹武器系统各类可靠性指标的检验与评估等方面,特别是为小样本条件下导弹可靠性指标评定提供了一种可信的解决方案。随着Bayes理论应用的不断深入,其起到的减少试验子样、缩短试验周期、增加试验效益的作用是不言而喻的,在这一过程中取得的某些成果已被相关国军标收录,例如:从1994年颁布的GJBZ20217-94到2009年颁布的GJB6671-2009[1]等系列有关导弹武器系统设计定型试验规程中,均引用了相同的简单假设下导弹单发命中概率指标Bayes检验方法,此种方法有着计算简单、工程应用方便等特点,但随着实际应用的加深,发现其存在瑕疵,有进一步改进的余地,下面就其存在的问题及解决办法展开深入探讨。
1 简单假设Bayes检验方法
在海防战术导弹设计定型试验中,导弹射击方案的制定通常是基于单发命中概率指标的检验方案。当试验子样较少或者应用经典法制定检验方案将导致双方风险偏大时,一般采用Bayes方法来制定检验方案,下面给出以往规程中简单假设下对导弹单发命中概率指标θ的Bayes检验方法。
对于统计假设:

其中,参数空间Θ=Θ0+Θ1。
决策不等式为:
其中,d=(1-θ1)/(1-θ0)为鉴别比,λ=θ1/θ0为鉴别系数,sn为试验成功数,fn为试验失败数。
验前概率为:

其中,n0为验前试验数,s0为验前成功数。
检验过程中,生产方Bayes风险απ0、使用方Bayes风险βπ1为:

式(2)中,α和β分别为经典的生产方风险和使用方风险,且有:

在制定检验方案时,应使απ0与βπ1相当。
2 问题分析
“当产品设计过程结束,完成了从设计到工艺生产的转化,于是理论上可以据此生产无限多产品,就是我们要考察的全体,其某一质量特性服从某个总体分布。”[2],海防战术导弹设计定型亦符合这一过程,所以在导弹设计定型试验中对导弹产品的检验属于抽样检验,根据产品质量抽样检验原理[3],当导弹单发命中概率θ不低于AQL(合格质量水平,取为θ0)或θ≥θ0时,定型试验成功;当θ不高于LQ(极限质量水平,取为θ1)或θ≤θ1时,定型试验失败。
根据统计决策理论[4],在上述导弹产品检验过程中的Bayes风险r(π,a)由下式决定:
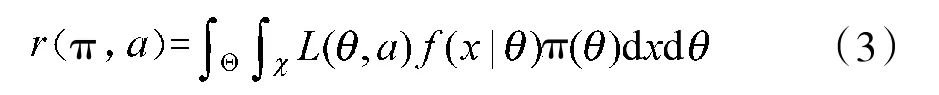
其中,Θ为参数空间,χ为样本空间,θ为导弹质量特征参数,a为采取的行为或决策,L(θ,a)为损失函数,f(x|θ)为似然函数,π(θ)为先验概率密度函数。
在以往规程给出的简单假设Bayes检验方案中,有下式成立:

其中,χ0为接收产品的样本空间,χ1为拒收产品的样本空间,ai为接收假设Hi的行为或决策。
将式(4)代入式(3),可得简单假设Bayes风险,即有式(2)成立。
在简单假设Bayes检验方法中,式(4)是对导弹设计定型试验实际情况的数学抽象,其参数空间只包含两点即Θ={θ0,θ1},显然与实际不符,致使其损失函数有可能存在系统偏差。
从检验风险或损失角度而言,产品质量的合格标准是唯一的,即当θ≥θ0时产品检验结果合格接收此批产品,则此决策对使用方而言是没有损失的;当θ<θ0时产品检验结果不合格拒收此批产品,则此决策对生产方而言是没有损失的,反之都是有损失的。风险或损失正是由于非全额检验造成的。据此,在制定检验方案时应有下式成立:
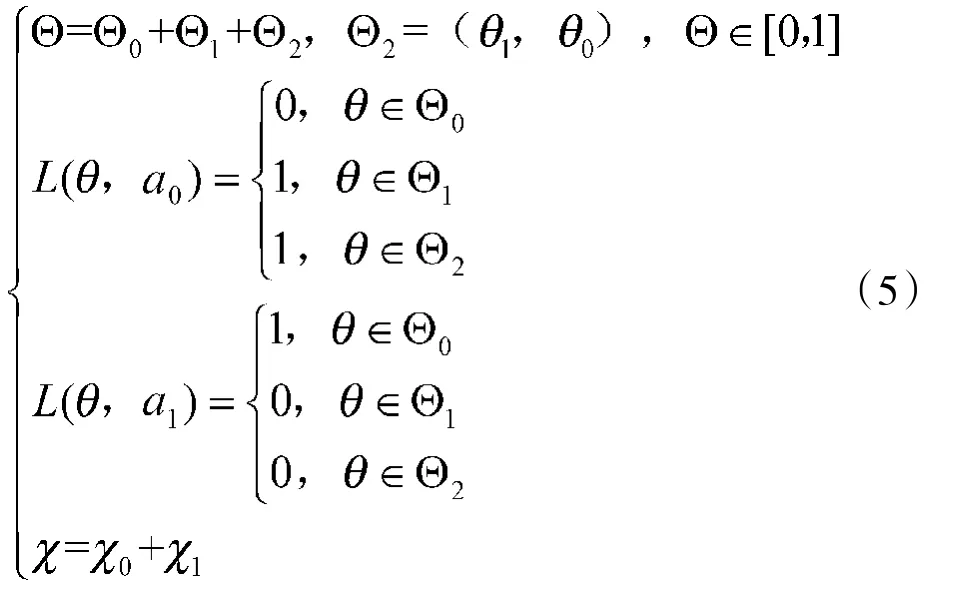
其中,a0:接收假设H0,a1:接收假设H1。
将式(5)代入式(3),可得复合假设生产方Bayes风险απ00和使用方Bayes风险βπ11为:

GJB6671-2009规定在导弹指标的检验过程中要坚持双方风险相当的原则,所以风险的计算对于确定试验样本量是至关重要的,同时也涉及到试验的公平性。简单假设Bayes检验方法的统计假设与导弹飞行试验实际有出入,其无法考虑θ∈(θ1,θ0)时决策所带来的损失,导致Bayes风险可能存在系统偏差,而复合假设Bayes检验方法可以有效解决这一问题。
3 复合假设Bayes检验方法
复合假设Bayes检验方法,设有统计假设:

π(H0|X)与π(H1|X)为θ的后验概率,决策不等式为:

其中,

θ的后验概率密度π(θ|x)由下式决定[5]:

其中,fn为试验失败数,n0、s0和sn定义同前,B(a,b)为贝塔函数。
θ的先验概率π(θ)由下式决定[5]:

将似然函数π(x|θ)、式(5)和式(9)代入式(6),可得到生产方Bayes风险απ00和使用方Bayes风险βπ11。
在制定检验方案时,应使απ00和βπ11相当。
4 案例分析
采用GJB6671-2009给出的范例。假设某型导弹设计定型试验,其单发命中概率θ的合格质量水平θ0=0.75,极限质量水平θ1=0.58,且有导弹研制试验结果作为先验信息(n0,s0)=(8,6),利用简单假设 Bayes检验方法制定的检验方案为(sn,fn)=(5,2),即定型试验7发5中合格,经计算双方风险απ0=0.151 0、βπ1=0.140 9,基本相当。
试根据以上数据制定复合假设Bayes检验方案,并比较两方案的Bayes风险。
解:已知θ0=0.75,θ1=0.58,s0=6,f0=2,当导弹定型试验样本量n=6、7、8时,在满足式(7)的条件下,可以得到相应的检验方案(sn,fn)下的Bayes风险,计算结果见表1。
本案例用Matlab编程计算,计算过程中的积分值由int()函数求取。
从表1的计算结果可以得到以下两点结论:
①对于相同的检验方案,简单假设的生产方Bayes风险απ0要大于复合假设的生产方Bayes风险απ00;简单假设的使用方Bayes风险βπ1要小于复合假设的使用方Bayes风险βπ11。

表1 导弹单发命中概率两种检验方案Bayes风险比较
②按照双方风险相当的原则,用简单假设Bayes检验方法选择的检验方案为(sn,fn)=(5,2),即定型试验7发5中合格;用复合假设Bayes检验方法选择的检验方案为(sn,fn)=(5,1),即定型试验6发5中合格。
以上两点说明:从Bayes风险或试验公平性角度而言,用以往规程给出的简单假设Bayes检验方法来制定检验方案,相比较用复合假设Bayes检验方法来制定检验方案,增大了生产方Bayes风险,使最终检验结果照顾了生产方利益,但损害了使用方利益。
5 结论
理论和实例分析表明,复合假设Bayes检验方法相较以往规程中给出的简单假设Bayes检验方法更加符合海防战术导弹飞行试验的实际情况,相比较而言是科学合理的,特别是其损失函数的确定方法对经典假设检验也有重要借鉴意义。
对于服从非二项分布的可靠性指标的复合假设检验,只是似然函数、先验函数及后验函数和二项分布有所不同,所得结论不变。
[1]李守秀.GJB 6671-2009反舰导弹定型试验规程[S].北京:中国人民解放军总装备部,2009.
[2]何国伟.可靠性试验技术[M].北京:国防工业出版社,1995.
[3]马毅林,于振凡.产品质量抽样检验[M].北京:中国标准出版社,1997.
[4]James O B.Statistical Decision Theory and Bayesian Analysis[M].New York:SVNY Publishing,1980.
[5]周源泉,翁朝曦.可靠性评定[M].北京:科学出版社,1990:66.
[6]茆诗松,王玲玲.可靠性统计[M].南京:华东师范大学出版社,1985.
Method for Bayesian Hypothesis Testing of Missile Reliability Indexes under Complex Hypothesis
ZHEN Xin1,DING Li-jun2
(1.Unit 93 Troop 92941 of PLA,Huludao 125000,China;2.Unit 98 Troop 92493 of PLA,Huludao 125000,China)
For a long time,a null hypothesis and its resistant hypothesis have been adopted the form of a point hypothesis which may increase Bayes risk of users when Bayesian hypothesis testing for the reliability indexes of the Navy tactic missile has been conducted in the test of missiles.In this article,the reason of the growth of Bayes risk of users has been clarified theoretically.Meantime,a complex hypothesis has been given up,and its advantages over a point hypothesis have been vindicated by example.
a Point Hypothesis,complex hypothesis,classical risk,Bayesian risk
E917
A
1002-0640(2014)10-0183-03
2013-07-09
2013-09-07
甄 昕(1970- ),男,高级工程师。研究方向:导弹武器系统可靠性试验。

