穿斗式木构架抗震特性分析
黄 舜傅宇光
(同济大学建筑工程系,上海200092)
穿斗式木构架抗震特性分析
黄 舜*傅宇光
(同济大学建筑工程系,上海200092)
对穿斗式木构架结构部件组成、房屋结构尺寸设计、施工工艺、结构受力等进行了分析。在此基础上,建立了穿斗式木构架房屋的抗震计算模型,进行了地震荷载作用下的结构时程动力计算,研究并分析了此类结构形式的抗震性能。分析结果表明:穿斗式木构架最大位移响应是随着榫卯节点刚度的增加而减小的,随着输入地震波加速度峰值增大,榫卯节点刚度变化对木构架中柱柱顶位移峰值的影响也逐渐增大。
穿斗式木构架,数值模型,抗震特性,动力时程分析
1 引 言
穿斗式木构架房屋是我国传统建筑结构形式之一,在我国广大农村其应用依然非常普遍,其穿枋与柱子的连接依靠榫卯节点,为半刚性连接。2008年5月12日,四川汶川发生里氏8.0级特大地震,灾区许多建筑物受到严重破坏,但穿斗式木构架体现出了较好的抗震性能[1,2]。穿斗式木构架以每个檩子下用支柱支撑为原则,穿枋连接横向柱子成排架,斗枋连接纵向柱子,檩子上是椽子,椽子上是瓦片。屋顶重量通过椽子、檩子和支柱到达地面。
本文研究穿斗木结构房屋的抗震性能,通过建立有限元计算模型,分析研究结构特征和动力性能,以供穿斗木结构房屋的建造和维护加固作参考。
2 穿斗式木构架房屋数值模拟
采用SAP2000分析模型,结构及构件材料属性分别定义为各向同性、正交各向异性和各向异性[3,4]。
2.1 房屋结构计算模型为
其横向柱子由穿枋连接,纵向柱子由斗枋连接,柱、枋采用直榫连接。模型木柱安放在带凹孔的混凝土基座内[5,6],木板墙体通过抱柱与柱子连接,通过榫卯与上下穿枋连接。在数值模拟中,柱、枋选用线单元模拟,墙体选用壳单元模拟,柱、枋之间的榫卯节点采用连接单元模拟。数值模型采用1/2缩尺模型,尺寸如图2所示。墙体根据其几何和受力特点选用四节点的四边形单元模拟。
2.2 框架单元的计算参数为
截面几何尺寸如表1所示。木材弹性模量E、密度ρ、泊松比μ等按照含水率10%的杉木取值:ρ=269 kg/m3,E1=12 200 MPa,E2=1 220 MPa,E3=610 MPa,μ12=0.37,μ13=0.47,μ23=0.43,G12=915 MPa,G13=732 MPa,G23=219.6 MPa。其中,下标1、2和3分别为木材的L、T和R方向(图1)。

表1 构件尺寸Table 1 Size of the elements
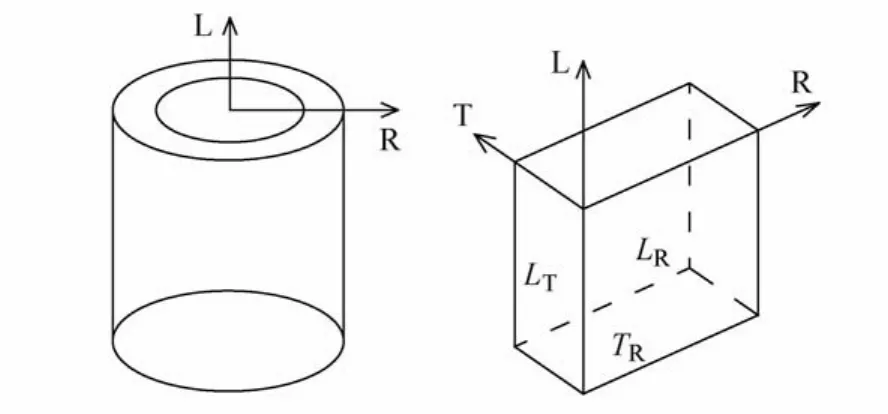
图1 木材正交三向轴图Fig.1 The orthogonal three-axis of the wood
连接单元的属性假定由6个内部“弹簧”组成,依次对应每个内部自由度。图3显示了弹簧的轴向、剪切和纯弯的3种变形,其中,剪切和纯弯位于1-2平面内。其他3个没有显示的弹簧的变形方式为位于1-3平面内的扭转、剪切和纯弯。模型采用多段线性随动硬化塑性属性。
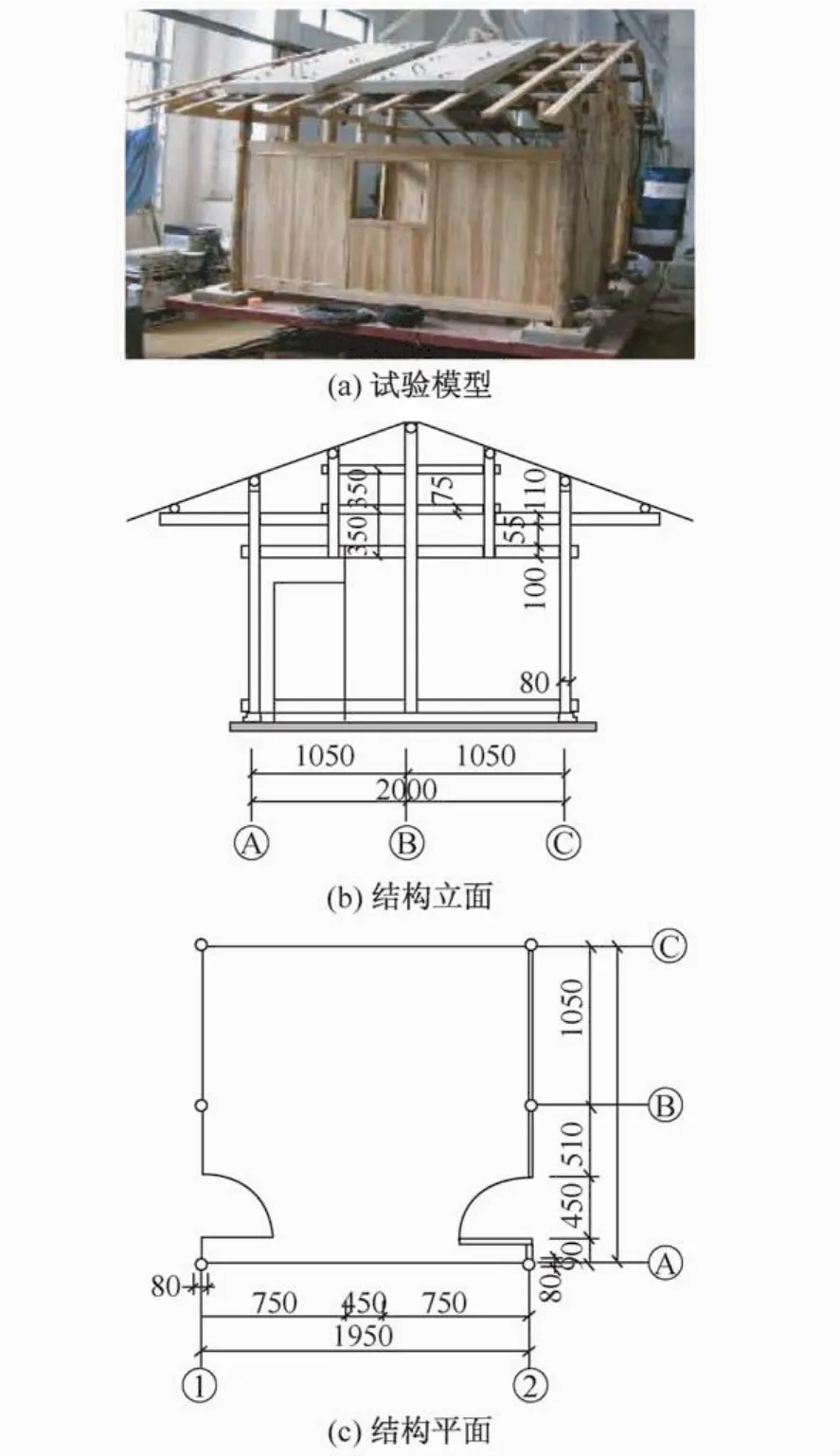
图2 模型构件尺寸及布置Fig.2 Model size and structural element arrangement
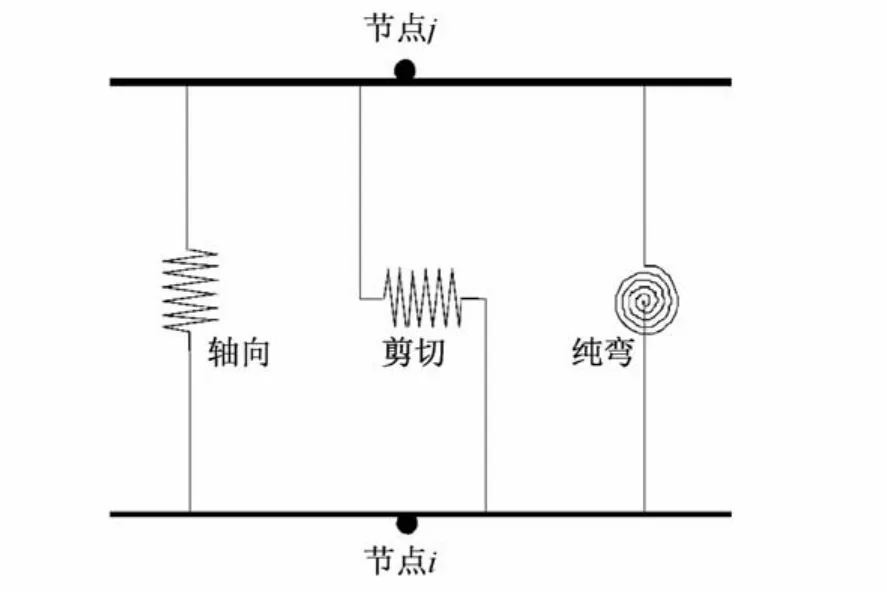
图3 连接单元中的3个非线性弹簧Fig.3 Three nonlinear springs of the connecting unit
房屋的所有榫卯节点简化分为A型节点和B型节点,如图4所示。
榫卯节点的半刚性性质已得到广泛认同[7]。在数值模拟时对此连接的模拟均为引入无质量、无尺寸的虚拟单元加在梁单元的两端。数值模拟中节点采用连接单元MultiLinear Plastic,轴向和侧向刚度取以往研究中采用的较大刚度值109N/mm;扭转刚度根据文献有限元分析[8]得到的弯矩-转角关系图中的三个关键点分别确定(表2),采用交互方式输入SAP2000程序中,并选取Kinematic模型分析。

图4 穿斗式木构架房屋榫卯节点Fig.4 Tenon joints of the Chuan-Dou style wood frame house
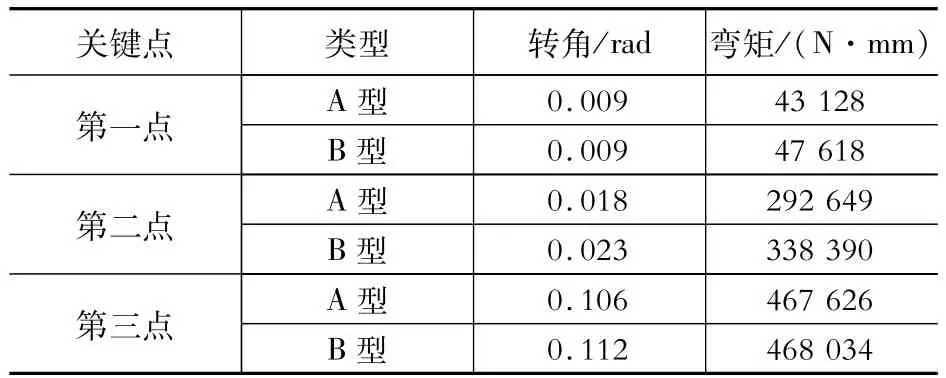
表2 榫卯节点的弯矩-转角曲线特征点Table 2 Key points of themoment-rotation curve in tenon joints
地震作用下,若地震水平加速度小于μmg(μ为静摩擦系数,不考虑竖向地震影响),柱与柱础间无滑移;反之,柱脚会相对柱基础发生水平滑移。柱根与基础石间摩擦系数取0.6。模型上部结构总重约为1 500 N,数值模拟时,用连接弹簧模拟柱脚与柱础间滑移作用,f′=kx,其中,k为弹簧刚度系数,x为位移。假定x为单位位移,则f′=k,且分配到每一根柱子上的摩擦力f′=1/6f,代入数据,得k=150 N/mm。将柱脚处支座约束简化为固定铰支座。木结构阻尼比取0.02。
结构整体数值模拟采用非线性动力时程计算方法,加载地震波与试验相同,采用1940年美国加州地震El-Centro波,分0.1 g、0.2 g、0.3 g、0.4 g和0.5 g共5个工况加载。计算完成后提取前6阶模态,结果如表3所示。
图5-图7为不同峰值加速度输入下中柱位移的数值模拟值与试验值的比较。表4为相应水平地震波下,中柱位移最大值的计算结果与试验值的比较。计算结果和试验基本吻合。本文通过测量柱底、柱顶的位移峰值来评价结构在不同加速度下的地震响应。
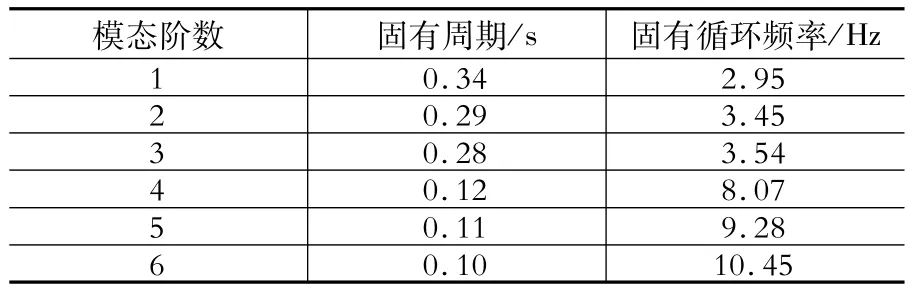
表3 穿斗式木构架自振周期及频率Table 3 Vibration periods and frequencies of the Chuan-Dou style wood frame house
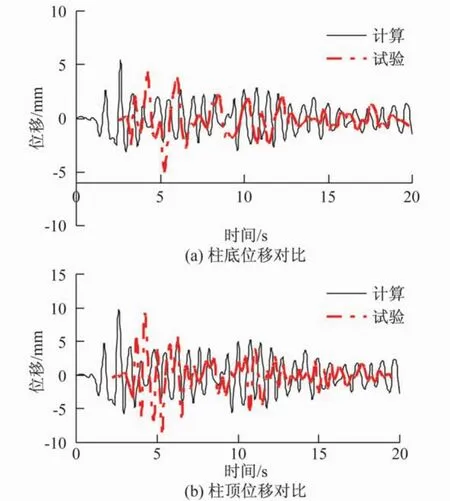
图5 0.2 g输入加速度时中柱位移的比较Fig.5 Comparison of the column displacement at the 0.2 g the input acceleration

图6 0.3 g输入加速度时中柱位移的比较Fig.6 Comparison of the column displacement at the 0.3 g input acceleration
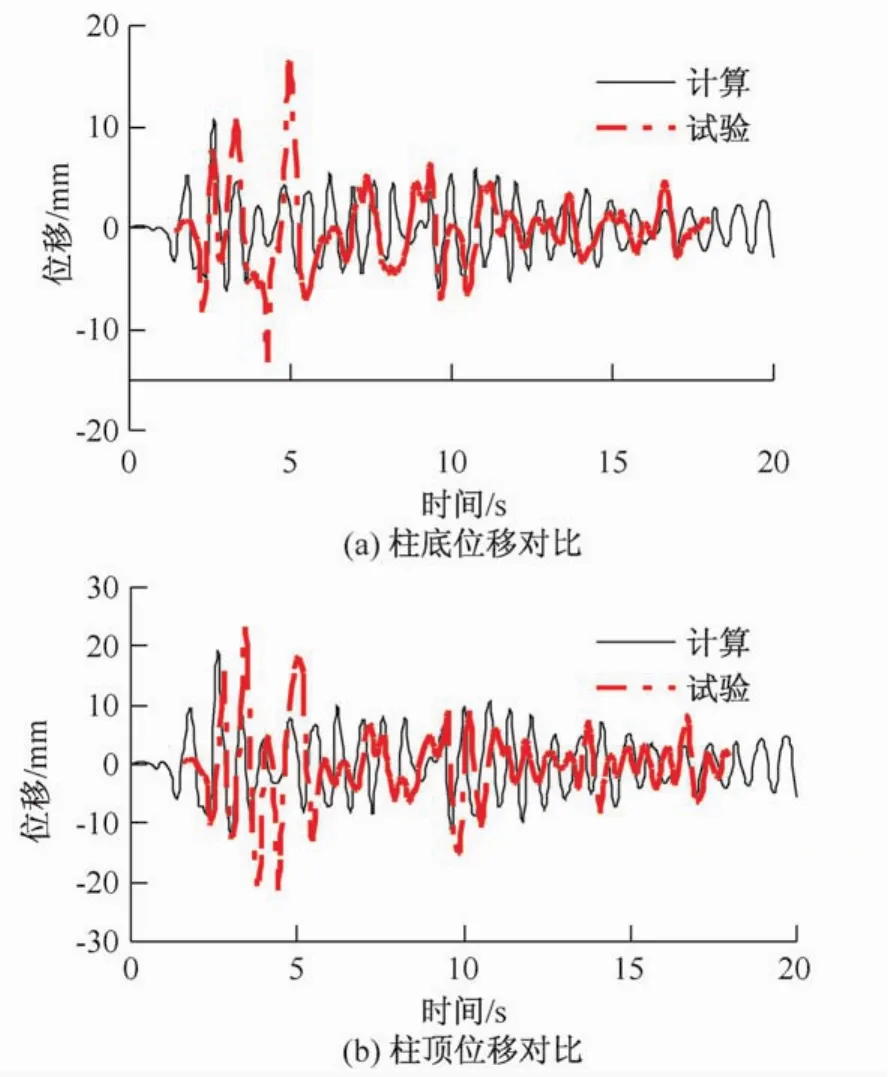
图7 0.4 g输入加速度时中柱位移的比较Fig.7 Comparison of the column displacement at 0.4 g the input acceleration
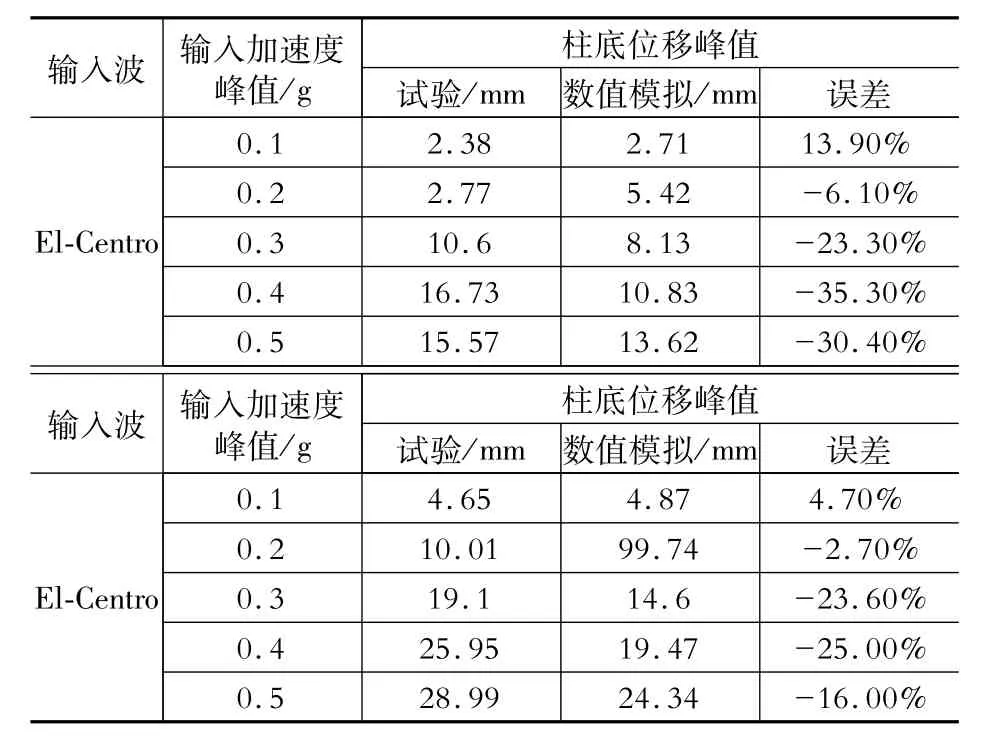
表4 中柱最大位移比较Table 4 Com parison of themax column displacement
3 榫卯节点对结构地震反应影响分析
前述数值模拟中榫卯节点采用MultiLinear Plastic连接单元[9],其弯矩-转角关系考虑非线性。为简化计算,以线性连接单元代替非线性连接单元,并对比分析两种节点模拟方式对整个穿斗式木构架结构的差异。线性连接单元转动刚度以A、B型节点刚度平均值为依据,取弯矩-转角关系中加载前半段刚度1.4×107N·mm/rad。采用线性连接单元与非线性连接单元两种计算模型得到的位移时程见图8。线性和非线性连接单元模型计算结果之比显示:两种模型计算的位移时程几乎无差别。比较结果表明,在适当选取榫卯节点转动刚度的情况下,将非线性连接单元简化为线性连接单元模拟计算可满足精度要求。

图8 0.1 g,0.4 g工况线性和非线性连接单元模型计算的柱顶位移比较Fig.8 Comparison of the column top displacement for linear and nonlinear joints(0.1 g,0.4 g)
为了解榫卯节点转动刚度与穿斗式木构架自振频率的关系,改变节点转动刚度,计算木构架相应自振频率,可得到木构架自振频率随节点转动刚度的变化情况,见图9。

图9 穿斗式木构架自振频率随节点转动刚度变化Fig.9 The variation of natural vibration frequencies at different rotational node stiffness in the chuan-dou style wood frame house
计算结果显示(图9),榫卯节点接近于铰接时(转动刚度为103N·mm/rad)与榫卯节点接近于固接时(转动刚度为1011N·mm/rad)穿斗式木构架前3阶自振频率分别相差0.43 Hz、0.37 Hz和0.22 Hz。穿斗式木构架自振频率随榫卯节点刚度变化而变化,榫卯节点刚度为107-109N·mm/rad的范围内,自振频率随节点刚度变化较敏感,木构架自振频率随节点刚度变化迅速变化,此范围之外,木构架自振频率变化小。
为研究榫卯节点转动刚度对穿斗式木构架地震反应的影响,在103-109N·mm/rad范围内改变榫卯节点转动刚度,以EL-Centro波为加载地震波进行0.1 g、0.3 g、0.5 g共3个工况的动力时程分析。
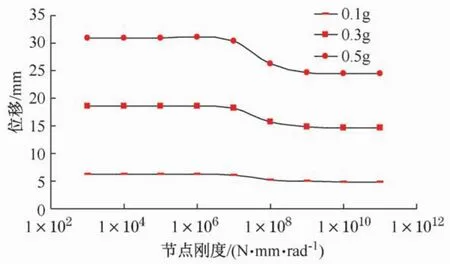
图10 中柱柱顶位移峰值随节点转动刚度变化情况Fig.10 Column top displacement variation at the different nodal rotational stiffness
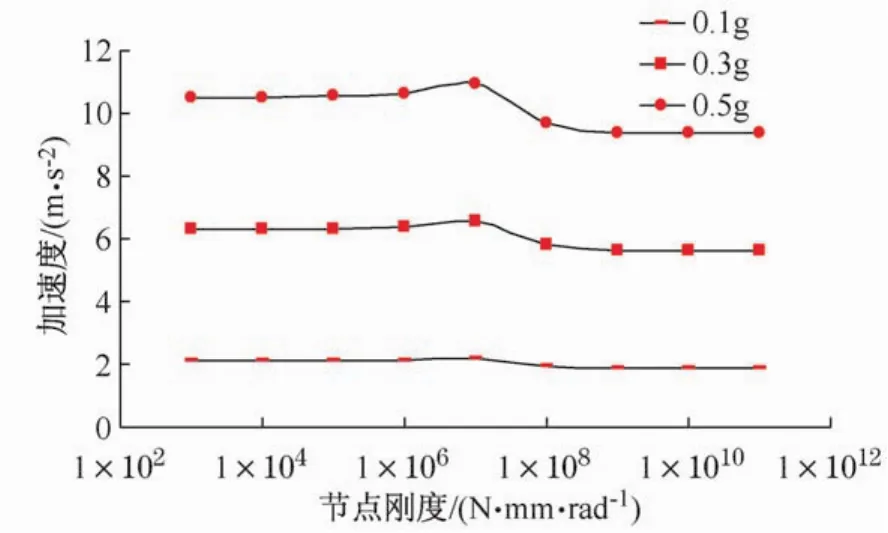
图11 中柱柱顶加速度峰值随节点转动刚度变化情况Fig.11 The column top acceleration variation at different nodal rotational stiffness
图10为计算所得各工况下穿斗式木构架中柱柱顶位移峰值随榫卯节点转动刚度变化情况,图11为计算所得各工况下穿斗式木构架中柱柱顶加速度峰值随榫卯节点转动刚度变化情况。架最大位移随节点刚度变化存在一敏感区,榫卯节点刚度为107-109N·mm/rad的区段中,木构架最大位移随节点刚度增大而迅速减小;敏感区以外,木构架最大位移随节点刚度增大而缓慢减小或保持稳定。②随着输入地震波加速度峰值的增大,榫卯节点刚度变化对穿斗式木构架中柱柱顶位移峰值的影响逐渐增大。
从图11可知:①输入地震波加速度峰值为0.1 g的工况下,穿斗式木构架中柱柱顶最大加速度随榫卯节点转动刚度增大而增大;②输入地震波加速度峰值为0.3 g和0.5 g的工况下,穿斗式木构架中柱柱顶最大加速度随榫卯节点转动刚度的增大先增大后减小,存在峰值。可能是因穿斗式木构架自振周期与地震波频谱出现耦合导致。③节点是否破坏可以通过测量节点的极限弯矩来进行评判。除了构架的加速度以外,若中柱的柱顶、柱底的相对位移角过大,则也可以此分析房屋的破坏,总结破坏特征。
4 结 论
(1)在适当选取榫卯节点转动刚度的情况下,将非线性连接单元简化为线性连接单元模拟计算可满足精度要求。
(2)穿斗式木构架自振频率随榫卯节点刚度的变化而变化,且存在一敏感区。敏感区内,木构架自振频率随节点刚度变化而迅速变化;敏感区外,木构架自振频率变化小,基本等于节点铰接或固接时木构架的自振频率。
(3)穿斗式木构架地震反应最大位移随榫卯节点刚度增加而减小,且当输入地震波加速度峰值增大时,节点刚度变化对穿斗式木构架中柱柱顶位移峰值的影响逐渐增大。
致谢 本课题由上海市大学生创新训练计划资金支持,由同济大学陈世鸣教授悉心指导,在此谨向陈老师及同济大学上海市大学生创新训练计划致以谢意!
[1] 同济大学土木工程防灾国家重点实验室.汶川地震震害研究[M].上海:同济大学出版社,2011.State Key Laboratory for Disaster Reduction in Civil Engineering,Tongji University.Analysis of the characteristics of the great Wenchuan earthquake[M].Shanghai:Tongji University Press,2011.(in Chinese)
[2] 吕西林,李建中,唐益群,等.5·12汶川地震后同济大学技术人员在四川广元房屋应急评估工作概况及体会[J].结构工程师,2008,24(3):1-2.Lu Xilin,Li Jianzhong,Tang Yiqun,et al.Summary and comments on building damages by Sichuan 5·12 earthquake based on site urgent structural evaluation.[J].Structural Engineers,2008,24(3):1-2.(in Chinese).
[3] CSI公司.CSI分析参考手册[M].2004.Computers and Structures Inc.CSIanalysis reference manual[M].2004.(in Chinese)
[4] 北京金土木软件技术有限公司.SAP2000中文版使用指南[M].北京:人民交通出版社,2009.Beijing Civil King Software Technology Co.,Ltd.User guide for SAP2000(Chinese version)[M].Beijing:China Communications Press,2009.(in Chinese)
[5] 黄玲,陈世鸣.穿斗式木构架房屋中的榫卯节点性能研究[J].中国科技论文在线,2011.Huang Ling,Chen Shiming.Study ofmechanical performance of tenon andmortise joint in chuan dou-style(or column and tie joint)wood[J].Sciencepaper Online,2011.(in Chinese)
[6] 黄曙.农村典型木结构房屋的抗震性能及加固措施研究[D].长沙:湖南大学,2009.Huang Shu.Study on the seismic behaviors and strengthing measures of typical rural wooden house[D].Changsha:Hunan University,2009.(in Chinese)
[7] 赵正易,化明星.印尼木结构房屋连接概述[J].结构工程师,2012,28(5):177-182.Zhao Zhengyi,Hua Mingxing.Introduction to Indonesia wood structure connections[J].Structural Engineers,2012,28(5):177-182.(in Chinese)
[8] 黄玲.穿斗式木构架房屋抗震性能研究[D].上海:同济大学,2011.Huang Ling.Study on seismic performance of chuan dou-style(column and tie joint)wood frame house[D].Shanghai:Tongji University,2011.(in Chinese)
[9] 邓大利,陆伟东,居兴鹏.木结构榫卯节点耗能加固有限元分析[J].结构工程师,2011,27(4):62-66.Deng Dali,Lu Weidong,Ju Xinpeng.Finite element analysis of energy dissipation reinforcement for mortise and tenon joints[J].Structural Engineers,2011,27(4):62-66.(in Chinese)
Study of Seism ic Characteristic of a Chuan-Dou Style(or Column and Tie Joint)W ood Frame House
HUANG Shun*FU Yuguang
(Department of Building Engineering,Tongji University,Shanghai200092,China)
In this paper,the structural components,construction technology and structural capacity of the Chuan-Dou style(or column and tie joint)wood frame houses were summarized and analysed.A FE model was established for a Chuan-Dou stylewood frame house.The time dynamic response analysis of the structures under seismic input was executed.The seismic performance of such a wood frame houses was investigated.Analyses showed that themax displacementof the Chuan-Dou stylewood frame house decreaseswhen the stiffness of the tenon joint nodes increases.With the increase of the max value of the input accelerations of the seismic waves,the influence of the the tenon joint node stiffness increases on the column top displacement of the wood frame house.
chuan-dou stylewood frame,numericalmodel,seismic performance,dynamic time-history analysis
2013-03-28
*联系作者,Email:huangshunhs@gmail.com

