点源模型在旋转声源声场计算中的推广应用

付建，王永生

（海军工程大学动力工程学院，湖北武汉430033）

点源模型在旋转声源声场计算中的推广应用

付建，王永生

（海军工程大学动力工程学院，湖北武汉430033）

针对螺旋桨、喷水推进器、风扇等旋转机械，研究了基于点源模型的旋转声源负载噪声频域预报方法。结合点源模型理论，将旋转声源离散为均匀分布在运动轨迹上的有限个固定声源，各声源间时域的迟滞时间转换为频域的相位差，所有点声源声场的总和即为旋转声源的声场。结合自由空间旋转点源和旋转力源声场仿真计算，验证了旋转声源离散方法的准确性；计算分析了不同半径、不同频率旋转声源对离散点数的要求；以单个螺旋桨叶片为对象，提出了叶片表面旋转力源按声场网格离散和分块离散的方法，并验证了离散方法的有效性，为点源模型在旋转声源声场中的推广应用提供了前提。

点源模型；旋转声源；负载噪声；离散点数；离散方法

以离心泵、螺旋桨等为代表的旋转机械在舰船上应用广泛，旋转机械的共同特点是其主要做功部件（叶轮）噪声对应为旋转声源声场。文献［1-4］推导了简单旋转点声源声场的解析解；文献［5-9］利用点源理论分析了管道内旋转声源声场的数值解。本文在借鉴前人研究的基础上，将点源模型推广应用到任意边界条件下旋转声源频域声场的数值计算，能够较为真实的模拟幅值、相位随时间变化的旋转声源声场特性。

1 旋转声源的离散方法

将每个旋转声源（点源或偶极源）离散为沿旋转轨迹分布的一系列静止声源（见图1），每个声源在时域内乘以图2所示矩形函数（τ＝2πω0／M代表2个相邻分布声源之间的时间差，M为分布的静止声源个数，ω0为旋转速度），将所得时域声源进行傅里叶分解即得到频域声源，傅里叶变换后时域的延迟在频域表现为相位差，对所有静止点声源的频域辐射声场进行叠加即为对应的旋转声源声场。

图1 旋转声源离散示意图Fig.1 Sketch map of discrete rotating point source

图2 声源离散时域矩形函数Fig.2 Time rectangle function for source discretization

2 单个旋转声源的离散与验证

在用上述方法进行旋转声源噪声计算之前，有必要先对简单旋转声源声场进行计算和校核，本节验证了自由空间旋转点源和旋转偶极源的声场仿真计算。

2.1 旋转点源的仿真计算及验证

采用图3所示的球坐标系，点源在XY平面内旋转，坐标原点O取在其旋转中心处，Z为极轴。

图3 自由空间中点源旋转示意图Fig.3 Schematic plan of rotating point source in free space

设点源初始位置在rb处，观察点位于r0处。在任一时刻τ，设点源旋转到r处，若其旋转圆频率为ω0，则有φ＝φb+ω0τ，β为r0和rb之间的夹角。

假设声源是简谐的，即A0（ω）＝Qδ（ω-ωt），Q为源强度幅值，ωt为源频率。得到声压解［1］为

式中：n＝0时εn＝0.5，n≠0时εn＝1；k0＝ω／c，c为介质中声速；r＞、r＜分别为r和r0中的较大者和较小者；Pm（·）为勒让德函数；jm（·）为球贝塞尔函数；hm（·）为球汉克尔函数。

对于远场，取r0＝2 m，r＝0.3 m，φb＝0，φ0＝-π／4，ωt＝6 800 rad／s，ω0＝560 rad／s，c＝340 m／s。图4显示了旋转点源声场的仿真值和解析值的对比，图5对应n＝1，φ0＝-π／4时的声压指向性计算结果。

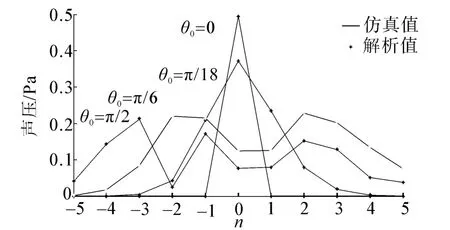
图4 声压幅值计算结果比较Fig.4 The comparison of acoustic amplitude

图5 声压指向性结果比较Fig.5 The comparison of acoustic directivity

2.2 旋转力源的仿真计算及验证

假设介质中一点x0处外加一激振力Fexp（jωt），计入外加力后声压的波动方程为

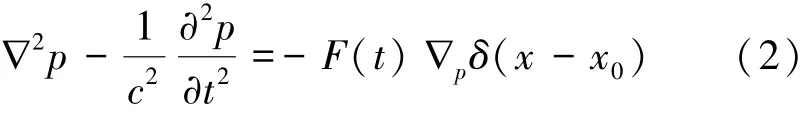
式中：∇p表示在声源点取梯度。式（2）与偶极子波动方程完全相同，因而由力激起的声场与偶极子声场也完全相同，只是以F（t）代替偶极距而已，这是力源等效为偶极子的理论基础［10］。力源与偶极矩的转换公式为［11］

式中：力F为矢量，偶极矩方向与力源方向相同；Z0为声场介质阻抗。对于CFD得出的结果，也就是单元网格上的压强脉动，可以类比为集中在网格中心的点力，方向为单元法线方向，大小为压强乘以网格面积。

旋转力源在XY平面运动，运动示意图见图6（a），力源Z方向幅值F＝1 N，旋转直径D＝0.3 m，声速c＝340 m／s，旋转角速度ω＝10.5 rad／s。垂直于旋转平面的圆周（半径为D）无量纲化声压（P∗＝PD2／F）指向性仿真结果同文献［7］计算值对比结果如图6（b）所示。

图6 旋转力源无量纲化声指向性Fig.6 Nondimensionalized acoustic directivity of rotating force

由图4～6可知旋转点源和旋转力源仿真结果与解析解或文献值在分析频段内吻合很好，这验证了旋转声源离散方法的准确性。

3 旋转声源对离散点数的要求

在对旋转声源进行离散时，离散点数会影响仿真计算的精度。单个声源离散点数取决于旋转速度（计算频率）和旋转半径。计算频率越高，旋转半径越大，所需的离散点数越多。

因偶极子可等效为幅值相同，振动方向相反、距离很近的2个单极子，并且单极子解析解容易得到，因此本节以单极子为对象，研究旋转半径和计算频率对离散点数的要求。

3.1 旋转半径对离散点数的要求

首先确定对仿真精度的要求，当仿真值与解析解相对误差即（Ps-Pa）／Pa≤0.025时（Ps为仿真解，Pa为解析解），认为仿真值满足精度要求。

分析旋转半径对离散点数的要求时，固定计算频率为500 Hz，依次改变旋转半径，分析不同半径对离散点数的要求（声源其余参数同2.1节），计算结果见表1。

表1 不同半径对离散点数的要求Table 1 The request of discretization points of different radiuses

由表1可知，随着旋转声源半径的增加，所需的离散点数越来越多，但不是线性增加；随着旋转声源半径增加，离散所需点数的增幅越来越小。

3.2 计算频率对离散点数的要求

分析计算频率对离散点数的要求时，固定旋转声源半径为0.5 m，分析不同计算频率对离散点数的要求，计算结果见表2。

表2 不同频率对离散点数的要求Table 2 The request of discretization points of different frequencies

由表2可知，随着计算频率增加，旋转声源离散所需点数逐渐增加，基本呈线性变化。

由表1、2中的结果可知，当半径与频率的增幅相同时，对应的离散点数增幅却不相同，离散点数对频率的变化更敏感，对旋转声源进行离散时要特别注意。

离散旋转声源时要满足2个条件：1）相邻2个声源之间的距离要小于最高分析频率对应声波波长的1／8～1／6，距离越小精度越高；2）对时域离散声源进行傅里叶变换后，其上限频率要高于分析频率；对于相同转速的点声源而言，离散点数决定了上限分析频率。分析频率升高时傅里叶变换所要求的离散点数增加，同时最高频率对应波长减小，亦要求离散点数增加，这是离散点数对频率的变化更敏感的原因所在。

4 叶片表面旋转力源的离散

旋转机械负载噪声是水动力噪声的主要成分，负载噪声又称偶极噪声，是由叶片表面压力脉动引起，计算旋转机械噪声时仅考虑叶片的负载噪声。

将瞬态流场计算时的脉动压力映射到对应的声场网格，则每一个声场网格单元上受到的非定常脉动力可以看成是一个旋转点力源，计算每个旋转点力源对应噪声，对所有面元积分即可得到整个旋转机械的运动声场。

本节以E779A船用螺旋桨单个桨叶为对象，介绍了叶片表面旋转力源与偶极子的等效离散过程，并将仿真计算结果与文献值进行比较。叶轮表面旋转力源的离散分为2种方法，方法1是将每个声场网格等效为1个旋转力源，方法2是借鉴Virtual Lab风扇噪声计算方法，将桨叶沿径向和轴向方向分割为若干部分，每一部分等效为一个旋转力源，这样在保证计算精度的同时又能大幅提高计算速度。

本节螺旋桨流场瞬态计算所用模型已经过验证，具体内容文中不做详细介绍，螺旋桨几何、工作条件、声场计算参考值见文献［12-13］。

4.1 声网格对应旋转力源的离散

将叶片表面流场网格节点的脉动压力映射到声网格节点之后，进一步得到不同时刻每个单元面力在3个方向的分量，然后再将每个旋转力源离散为分布声源，离散时要注意每一时刻单元法向量都在变化。螺旋桨半径为0.113 m，最高分析频率为500Hz，根据表1可知当离散点取为30时，计算精度已能够满足要求。图7为一个旋转周期内某单元面力在3个方向分量的变化（Y为旋转轴）。图8（a）为单个桨叶的等效偶极子分布，图8（b）为单个桨叶的等效旋转偶极子分布。

由图7可知，对于该型桨而言，单元面力的轴向分量要高于径向分量，并且面力的径向的分量在一个旋转周期内亦完成一个周期变化，轴向分力脉动幅值很小。

对所有偶极子辐射声场进行叠加，即可得到单个桨叶的负载噪声，测点位于桨盘面内距离叶梢2倍螺旋桨半径处；文献［13］计算了该桨单个桨叶的时域负载噪声，对时域噪声进行傅里叶变换，并将仿真值同其比较，见图9（参考声压为10-6Pa）。由图9可知在分析频段内，计算值和文献值吻合较好，尤其是在低频，方法的准确性得到了验证。

图7 不同时刻面元点力在3个方向的分量Fig.7 The point force of element at different time in three directions

图8 单个桨叶等效离散偶极子Fig.8 Equivalent discrete dipoles of single blade

图9 单个桨叶负载噪声Fig.9 Loading noise induced by single blade

4.2 叶片表面旋转力源的分块离散

在4.1节中，划分叶片声网格时网格尺寸不仅要满足声场计算要求，又要保证脉动压力的映射精度。如果按照每个波长内6～8个声场单元的要求划分声网格，映射后的声网格节点压力脉动不能很好的体现实际叶片表面的脉动信息，尤其是导边等压力脉动幅值较大位置；如果尺寸过小，保证了数据映射精度的同时，等效的偶极子数目巨大，计算时对硬件的要求较高，计算时间过长，不利于该方法的推广应用。

声学软件LMS Virtual Lab在计算风扇噪声时，如果叶片尺寸同分析频率对应波长相比足够小时，将单个叶片作为紧致声源处理；如果叶片尺寸较大，整个叶片不能作为紧致声源处理时，可以将叶片沿弦长方向划分为若干部分，每一部分作为紧致声源处理；每个紧致声源等效为偶极子，通过设定风扇叶片数和转速求解风扇对应的线谱噪声［14］。

本文在借鉴Virtual Lab风扇噪声计算方法的基础上，将叶片沿径向和轴向划分若干部分，每一部分等效为一个偶极源，划分方法见图10。

图10 叶片划分示意图Fig.10 Schematic map of blade segmentation

每个力源对应的位置坐标Cjk和幅值Fijk为

式中：xj为声网格单元中心的不同坐标分量，j＝1，2，3分别对应为X、Y、Z方向；k代表不同部分编号，k＝1，2，..，m×n，NumElement为第k部分所包含的单元数；pi为单元压力，n＾ek为单元法向量，i对应时间步。

图11显示了2种划分方案对应的等效离散偶极子分布示意图。图12显示了不同划分方案对应的计算结果以及与4.1节结果的比较。

由图12可知，不同方案计算结果基本一致，部分频段略有差别。1×1方案在100～200 Hz与4.1节计算结果差别相对较大；2×2方案在150～250 Hz与4.1节计算结果差别相对较大；3×3方案在210 Hz处同4.1节计算结果差2.5 dB，4×4方案在210 Hz处同4.1节计算结果差1.1 dB，其余频率段吻合较好。以上结果表明如果用3×3或4×4方案对桨叶进行离散计算精度也是较高的。

由以上计算分析结果可知，采用分块离散方法对旋转叶片进行离散，在保证计算精度的同时能够大幅降低计算时间和对计算硬件条件的要求，有利于将点源模型理论进一步推广应用到大尺度旋转声源的高频声场计算。

图11 不同划分方案桨叶等效离散偶极子Fig.11 Equivalent discrete dipoles of different segmentation

图12 不同划分方案计算结果比较Fig.12 Results comparison of different segmentation

5 结论

1）单个幅值、相位随时间变化的旋转声源在频域内可以离散为沿运动轨迹分布的具有固定相位差的有限个静止声源，通过自由空间旋转声源声场仿真计算验证了旋转声源离散方法的准确性。

2）当旋转声源半径与分析频率的增幅相同时，准确模拟旋转声源声场所需的最少离散点数增幅并不相同，离散点数对频率的变化更敏感。

3）叶轮表面旋转力源可按声场网格和不同分块离散为偶极源，分块离散方法使得点源模型能够在旋转声源声场尤其是高频声场的计算中得以广泛应用。

4）将旋转声源离散方法应用于管道内旋转声源声场的准确计算与分析将是下一步的研究重点。

［1］吴九汇，陈花玲，黄协清.旋转点声源空间声场的频域精确解［J］.西安交通大学学报，2000，34（1）：71-75.WU Jiuhui，CHEN Hualing，HUANG Xieqing.Acoustic solution of rotating point source in frequency domain［J］.Journal of Xi′an Jiaotong University，2000，34（1）：71-75.

［2］LIU Zhihong.On acoustic radiation by rotating dipole sources in frequency domain［J］.Modern Applied Science，2011，5（5）：80-86.

［3］刘秋洪，黄曌宇，祁大同，等.圆管内旋转点声源声学频域分析［J］.西安交通大学学报，2004，38（5）：541-544.LIU Qiuhong，HUANG Zhaoyu，QI Datong，et al.Frequency domain solution of a rotating point source in an infinite duct［J］.Journal of Xi’an Jiaotong University，2004，38（5）：541-544.

［4］黄曌宇，刘秋洪，祁大同，等.封闭圆柱腔内旋转点声源声压的近场频域解［J］.应用力学学报，2004，21（2）：37-40.HUANG Zhaoyu，LIU Qiuhong，QI Datong，et al.Near field frequency domain solution of rotating point source in closed cylindrical cavity［J］.Chinese Journal of Applied Mechanics，2004，21（2）：37-40.

［5］DUNN M H，TWEED J，FARASSAT F.The application of a boundary integral equation method to the prediction of ducted fan engine noise［J］.Journal of Sound and Vibration，1999，227：1019-1048.

［6］何涛，钟荣，孙玉东.离心泵水动力噪声计算方法研究［J］.船舶力学，2012，16（4）：449-445.HE Tao，ZHONG Rong，SUN Yudong.Numerical method on hydrodynamic of centrifugal pump［J］.Journal of Ship Mechanics，2012，16（4）：449-445.

［7］CHOI H L，DUCK J L.Development of the numerical method for calculating sound radiation from a rotating dipole source in an opened thin duct［J］.Journal of Sound and Vibration，2006，295：739-752.

［8］马晓晶.管道内旋转声源辐射声场的数值计算方法研究［D］.北京：中国科学院，2009：11-14..MA Xiaojing.The numerical method of the sound field radiated from rotating source in duct［D］.Beijing：Chinese A-cademy of Sciences，2009：11-14.

［9］KUCUKCOSKUN K.Prediction of free and scattered acoustic fields of low-speed fans［D］.Ecully：Avenue Guy de Collongue，2012：22-26.

［10］马大猷.现代声学理论基础［M］.北京：科学出版社，2004：91-94.MA Dayou.Modern acoustic theory foundationl［M］.Beijing：Scientific Press，2004：91-94.

［11］CHANAUD R C.Tools for analyzing sound sources［EB／OL］.［2013-03-13］.CCR ASSOCIATE LLC，2010.http：／／www.ccrllc.com.

［12］TESTA C，SALVATORE F.Theoretical and numerical issues for hydroacoustic applications of the Ffowcs Williams Hawkings equation［C］／／26th AIAA Conference.［S.l.］，2005：1-13.

［13］魏应三.舰船水下辐射噪声数值计算方法研究［D］.武汉：海军工程大学，2012：219-222.WEI Yingsan.Research on numerical calculation method of underwater radiated noise of marine vessel［D］.Wuhan：Naval University of Engineering，2012：219-222.

［14］GERARD A，MOREAU S，BERRY A，et al.Acoustic modulation effect of rotation stator／rotor interaction noise［C］／／Proceedings of the Acoustics 2012 Nantes Conference.［S.l.］，2012：3781-3786.

Extended application of the point source model for the acoustic field solution of the rotating source

FU Jian，WANG Yongsheng
（College of Marine Power Engineering，Naval University of Engineering，Wuhan 430033，China）

In order to forecast the noise of circumvolve machines such as propellers，waterjets or pumps，the method of the point source model is studied to predict the loading noise of the rotating source in the frequency domain.The rotating source can be replaced by finite stationary sources distributing along the rotating trace，and the time difference between sources can be transformed into phase differences in the frequency domain.The sound field of the rotating source is equal to the summation of all of the point sources.The veracity of the discretization method is validated by the freedom sound field simulation of the rotating point source and rotating force source.And the requirement of the number of discrete points of the rotating source with a different radius and frequency is analyzed.Finally，taking the single propeller blade as the object，two discretization methods of blade rotating force are put forward.One method is to take each acoustic mesh as a single force source，and the other method is to divide the blade into segments and each segment can be taken as a single force source.The validity of these discretization methods has been validated，which can provide the precondition for the extended application of the point source model for the sound field calculation of the rotating source.

point source model；rotating source；loading noise；discrete point number；discretization method

10.3969／j.issn.1006-7043.201304020

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201304020.html

O42

A

1006-7043（2014）06-0719-06

2013-04-04.网络出版时间：2014-05-14 15：48：54.

国家自然科学基金青年基金资助项目（51209212）

付建（1985-），男，博士研究生；王永生（1955-），男，教授，博士生导师.

付建，E-mail：fujain_hgd＠163.com.